Bài 2:

a: =>2x^2-4x+1=x^2+x+5

=>x^2-5x-4=0

=>\(x=\dfrac{5\pm\sqrt{41}}{2}\)

b: =>11x^2-14x-12=3x^2+4x-7

=>8x^2-18x-5=0

=>x=5/2 hoặc x=-1/4

\(a,\left(x-1\right)\left(x+2\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\x+2=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-2\end{matrix}\right.\)

\(b,\left(x-2\right)\left(x-5\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x-2=0\\x-5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=2\\x=5\end{matrix}\right.\)

\(c,\left(x+3\right)\left(x-5\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x+3=0\\x-5=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=5\end{matrix}\right.\)

\(d,\left(x+\dfrac{1}{2}\right)\left(4x+4\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{1}{2}=0\\4x+4=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{1}{2}=0\\4\left(x+1\right)=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{2}\\x=-1\end{matrix}\right.\)

\(e,\left(x-4\right)\left(5x-10\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x-4=0\\5x-10=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=4\\x=2\end{matrix}\right.\)

\(f,\left(2x-1\right)\left(3x+6\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}2x-1=0\\3x+6=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}\\x=-2\end{matrix}\right.\)

`a,(x-1)(x+2)=0`

\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\x+2=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-2\end{matrix}\right.\)

`b,(x -2)(x -5)=0`

\(\Leftrightarrow\left[{}\begin{matrix}x-2=0\\x-5=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=5\end{matrix}\right.\)

`c,(x +3)(x -5)=0`

\(\Leftrightarrow\left[{}\begin{matrix}x+3=0\\x-5=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-3\\x=5\end{matrix}\right.\)

`d,(x + 1/2)(4x + 4)=0`

\(\Leftrightarrow\left[{}\begin{matrix}x+\dfrac{1}{2}=0\\4x+4=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{2}\\4x=-4\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{2}\\x=-1\end{matrix}\right.\)

`e,(x -4)(5x -10)=0`

\(\Leftrightarrow\left[{}\begin{matrix}x-4=0\\5x-10=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=4\\5x=10\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=4\\x=2\end{matrix}\right.\)

`f,(2x -1)(3x +6)=0`

\(\Leftrightarrow\left[{}\begin{matrix}2x-1=0\\3x+6=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}2x=1\\3x=-6\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}\\x=-2\end{matrix}\right.\)

`g,(2,3x -6,9)(0,1x -2)=0`

\(\Leftrightarrow\left[{}\begin{matrix}2,3x-6,9=0\\0,1x-2=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}2,3x=6,9\\0,1x=2\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=20\end{matrix}\right.\)

a.(x - 1)(x + 2)= 0

<=> x-1=0 hoặc x+2=0

<=> x=1 hoặc x=-2

b.(x -2)(x -5)=0

<=> x-2=0 hoặc x-5=0

<=> x=2 hoặc x=5

c.(x +3)(x -5)=0

<=> x+3=0 hoặc x-5=0

<=> x=-3 hoặc x=5

d.(x + 1/2)(4x + 4)=0

<=> x+1/2=0 hoặc 4x+4=0

<=> x=-1/2 hoặc x=-1

e.(x -4)(5x -10)=0

<=> x-4=0 hoặc 5x-10=0

<=> x=4 hoặc x=2

f.(2x -1)(3x +6)=0

<=> 2x-1=0 hoặc 3x+6=0

<=> x=1/2 hoặc x=-2

g.(2,3x -6,9)(0,1x -2)=0

<=> 2,3x-6,9=0 hoặc 0,1x-2=0

<=> x=3 hoặc x=20

Đề bài thiếu bạn ạ

3:

a: u+v=14 và uv=40

=>u,v là nghiệm của pt là x^2-14x+40=0

=>x=4 hoặc x=10

=>(u,v)=(4;10) hoặc (u,v)=(10;4)

b: u+v=-7 và uv=12

=>u,v là các nghiệm của pt:

x^2+7x+12=0

=>x=-3 hoặc x=-4

=>(u,v)=(-3;-4) hoặc (u,v)=(-4;-3)

c; u+v=-5 và uv=-24

=>u,v  là các nghiệm của phương trình:

x^2+5x-24=0

=>x=-8 hoặc x=3

=>(u,v)=(-8;3) hoặc (u,v)=(3;-8)

a) (x - 7)(2x + 8) = 0

\(\Leftrightarrow\left[{}\begin{matrix}x-7=0\\2x+8=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=7\\2x=-8\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=7\\x=-4\end{matrix}\right.\)

Vậy: S = {7; -4}

b) Tương tự câu a

c)  (x - 1)(2x + 7)(x² + 2) = 0

\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\2x+7=0\\x^2+2=0\end{matrix}\right.\)

Mà: x² + 2 > 0 với mọi x

\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\2x+7=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=1\\2x=-7\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-\dfrac{7}{2}\end{matrix}\right.\)

Vậy: \(S=\left\{1;-\dfrac{7}{2}\right\}\)

d) (2x - 1)(x + 8)(x - 5) = 0

\(\Leftrightarrow\left[{}\begin{matrix}2x-1=0\\x+8=0\\x-5=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}2x=1\\x=-8\\x=5\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}\\x=-8\\x=5\end{matrix}\right.\)

Vậy \(S=\left\{\dfrac{1}{2};-8;5\right\}\)

a/ Pt \(\Leftrightarrow\left[{}\begin{matrix}x-7=0\\2x+8=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=7\\x=-4\end{matrix}\right.\)

Vậy \(S=\left\{7;-4\right\}\)

b/ pt \(\Leftrightarrow\left[{}\begin{matrix}3x+1=0\\5x-2=0\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{3}\\x=\dfrac{2}{5}\end{matrix}\right.\)

c/ pt \(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\2x+7=0\end{matrix}\right.\) (\(x^2+2>0\forall x\))\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-\dfrac{7}{2}\end{matrix}\right.\)

d/ pt \(\Leftrightarrow\left[{}\begin{matrix}2x-1=0\\x+8=0\\x-5=0\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}\\x=-8\\x=5\end{matrix}\right.\)

a)(x-7)(2x+8)=0

⇔x-7=0 hoặc 2x+8=0

1.x-7=0⇔x=7

2.2x+8=0⇔2x=-8⇔x=-4

phương trình có 1 nghiệm x=7 và x=-4

b)(3x+1)(5x-2)=0

⇔3x+1=0 hoặc 5x-2=0

1.3x+1=0⇔3x=-1⇔x=-1/3

2.5x-2=0⇔5x=2⇔x=5/2

phương trình có 2 nghiệm x=-1/3 và x=5/2

a) Ta có: (5x-1)(x-3)<0

nên 5x-1 và x-3 trái dấu

Trường hợp 1:

\(\left\{{}\begin{matrix}5x-1>0\\x-3< 0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x>\dfrac{1}{5}\\x< 3\end{matrix}\right.\Leftrightarrow\dfrac{1}{5}< x< 3\)

Trường hợp 2:

\(\left\{{}\begin{matrix}5x-1< 0\\x-3>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x< \dfrac{1}{5}\\x>3\end{matrix}\right.\Leftrightarrow loại\)

Vậy: S={x|\(\dfrac{1}{5}< x< 3\)}

a) \(\left(3x-2\right)\left(4x+5\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}3x-2=0\\4x+5=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{2}{3}\\x=-\dfrac{5}{4}\end{matrix}\right.\)

Vậy: \(S=\left\{\dfrac{2}{3};-\dfrac{5}{4}\right\}\)

b) \(\left(2,3x-6,9\right)\left(0,1x+2\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}2,3x-6,9=0\\0,1x+2=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-20\end{matrix}\right.\)

c) \(\left(4x+2\right)\left(x^2+1\right)=0\)

Vì \(x^2+1\ge1>0\forall x\)

\(\Rightarrow4x+2=0\)

\(\Leftrightarrow x=-\dfrac{1}{2}\)

Vậy: \(S=\left\{-\dfrac{1}{2}\right\}\)

d) \(\left(2x+7\right)\left(x-5\right)\left(5x+1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}2x+7=0\\x-5=0\\5x+1=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{7}{2}\\x=5\\x=-\dfrac{1}{5}\end{matrix}\right.\)

Vậy: \(S=\left\{-\dfrac{7}{2};5;-\dfrac{1}{5}\right\}\)

e) \(\left(x-1\right)\left(2x+7\right)\left(x^2+2\right)=0\)

Vì \(x^2+2\ge2>0\forall x\)

\(\Rightarrow\left(x-1\right)\left(2x+7\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x-1=0\\2x+7=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-\dfrac{7}{2}\end{matrix}\right.\)

f) \(\left(3x+2\right)\left(x^2-1\right)=\left(9x^2-4\right)\left(x+1\right)\)

\(\Leftrightarrow\left(3x+2\right)\left(x-1\right)\left(x+1\right)-\left(3x-2\right)\left(3x+2\right)\left(x+1\right)=0\)

\(\Leftrightarrow\left[\left(3x+2\right)\left(x+1\right)\right].\left(x-1-3x+2\right)=0\)

\(\Leftrightarrow\left(3x^2+5x+2\right)\left(-2x+1\right)=0\)

\(\Leftrightarrow\left(3x^2+3x+2x+2\right)\left(-2x+1\right)=0\)

\(\Leftrightarrow\left[3x\left(x+1\right)+2\left(x+1\right)\right]\left(-2x+1\right)=0\)

\(\Leftrightarrow\left(x+1\right)\left(3x+2\right)\left(-2x+1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x+1=0\\3x+2=0\\-2x+1=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=-\dfrac{2}{3}\\x=\dfrac{1}{2}\end{matrix}\right.\)

Vậy: \(S=\left\{-1;-\dfrac{2}{3};\dfrac{1}{2}\right\}\)

a) Phương trình bậc hai

2 x 2   –   7 x   +   3   =   0

Có: a = 2; b = -7; c = 3;

Δ   =   b 2   –   4 a c   =   ( - 7 ) 2   –   4 . 2 . 3   =   25   >   0

Áp dụng công thức nghiệm, phương trình có hai nghiệm phân biệt là:

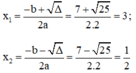
Vậy phương trình có hai nghiệm là 3 và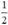 

b) Phương trình bậc hai  6 x 2   +   x   +   5   =   0

Có a = 6; b = 1; c = 5; 

Δ   =   b 2   –   4 a c   =   12   –   4 . 5 . 6   =   - 119   <   0

Vậy phương trình vô nghiệm.

c) Phương trình bậc hai  6 x 2   +   x   –   5   =   0

Có a = 6; b = 1; c = -5;

Δ   =   b 2   –   4 a c   =   12   –   4 . 6 . ( - 5 )   =   121   >   0

Áp dụng công thức nghiệm, phương trình có hai nghiệm phân biệt là:

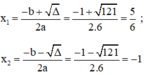
Vậy phương trình có hai nghiệm là -1 và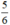 

d) Phương trình bậc hai  3 x 2   +   5 x   +   2   =   0

Có a = 3; b = 5; c = 2;

Δ   =   b 2   –   4 a c   =   5 2   –   4 . 3 . 2   =   1   >   0

Áp dụng công thức nghiệm, phương trình có hai nghiệm phân biệt là:

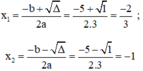
Vậy phương trình có hai nghiệm là -1 và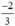 

e) Phương trình bậc hai  y 2   –   8 y   +   16   =   0

Có a = 1; b = -8; c = 16;  Δ   =   b 2   –   4 a c   =   ( - 8 ) 2   –   4 . 1 . 16   =   0 .

Áp dụng công thức nghiệm ta có phương trình có nghiệm kép :

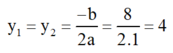
Vậy phương trình có nghiệm kép y = 4.

f) Phương trình bậc hai  16 z 2   +   24 z   +   9   =   0

Có a = 16; b = 24; c = 9;  Δ   =   b 2   –   4 a c   =   24 2   –   4 . 16 . 9   =   0

Áp dụng công thức nghiệm ta có phương trình có nghiệm kép:

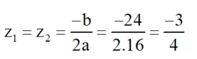
Vậy phương trình có nghiệm kép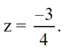 

Kiến thức áp dụng

Phương trình ax2 + bx + c = 0 (a ≠ 0) có biệt thức Δ = b2 – 4ac.

+ Nếu Δ > 0, phương trình có hai nghiệm phân biệt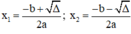 

+ Nếu Δ = 0, phương trình có nghiệm kép  ;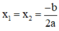

+ Nếu Δ < 0, phương trình vô nghiệm.

a. 2x\(^2\)-8=0

2x\(^2\)=8

x\(^2\)=4

x=2

b.3x\(^3\)-5x=0

x(3x\(^2\)-5)=0

\(\left[{}\begin{matrix}x=0\\x^2-5=0\end{matrix}\right.\)⇔\(\left[{}\begin{matrix}x=0\\x^2=5\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=^+_-\sqrt{5}\end{matrix}\right.\)

c.x+3x-4=0\(^{\left(\cdot\right)}\)

đặt t=x\(^2\) (t>0)

ta có pt: t\(^2\)+3t-4=0 \(^{\left(1\right)}\)

thấy có a+b+c=1+3+(-4)=0 nên pt\(^{\left(1\right)}\) có 2 nghiệm

t\(_1\)=1; t\(_2\)=\(\dfrac{c}{a}\)=-4

khi t\(_1\)=1 thì x\(^2\)=1 ⇒x=\(^+_-\)1

khi t\(_2\)=-4 thì x\(^2\)=-4 ⇒ x=\(^+_-\)2

vậy pt đã cho có 4 nghiệm x=\(^+_-\)1; x=\(^+_-\)2

d)3x\(^2\)+6x-9=0

thấy có a+b+c= 3+6+(-9)=0 nên pt có 2 nghiệm

x\(_1\)=1; x\(_2\)=\(\dfrac{c}{a}=\dfrac{-9}{3}=-3\)

e. \(\dfrac{x+2}{x-5}+3=\dfrac{6}{2-x}\)  (ĐK: x#5; x#2 )

⇔\(\dfrac{\left(x+2\right)\left(2-x\right)}{\left(x-5\right)\left(2-x\right)}+\dfrac{3\left(x+2\right)\left(2-x\right)}{\left(x-5\right)\left(2-x\right)}\)=\(\dfrac{6\left(x-5\right)}{\left(x-5\right)\left(2-x\right)}\)

⇒2x - x\(^2\) + 4 - 2x + 6x - 6x\(^2\) + 12 - 6x - 6x +30 = 0

⇔-7x\(^2\) - 6x + 46=0

Δ'=b'\(^2\)-ac = (-3)\(^2\) - (-7)\(\times\)46= 9+53 = 62>0

\(\sqrt{\Delta'}=\sqrt{62}\)

vậy pt có 2 nghiệm phân biệt

x\(_1\)=\(\dfrac{-b'+\sqrt{\Delta'}}{a}=\dfrac{3+\sqrt{62}}{-7}\)

x\(_2\)=\(\dfrac{-b'-\sqrt{\Delta'}}{a}=\dfrac{3-\sqrt{62}}{-7}\)

vậy pt đã cho có 2 nghiệm x\(_1\)=.....;x\(_2\)=......

câu g làm tương tự câu c

a, \(\left(x^2-5x+7\right)^2-\left(2x-5\right)^2=0\)

\(\Leftrightarrow\left(x^2-5x+7-2x+5\right)\left(x^2-5x+7+2x-5\right)=0\)

\(\Leftrightarrow\left(x^2-7x+12\right)\left(x^2-3x+2\right)=0\)

\(\Leftrightarrow\left(x-4\right)\left(x-3\right)\left(x-1\right)\left(x-2\right)=0\Leftrightarrow x=1;x=2;x=3;x=4\)

Vậy tập nghiệm phương trình là S = { 1 ; 2 ; 3 ; 4 } 

b, \(\left|2x-1\right|=5\Leftrightarrow\left[{}\begin{matrix}2x-1=5\\2x-1=-5\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-2\end{matrix}\right.\)

Vậy tập nghiệm của phương trình là S = { -2 ; 3 } 

c, \(\left|2x-1\right|=\left|x+5\right|\Leftrightarrow\left(2x-1\right)^2=\left(x+5\right)^2\)

\(\Leftrightarrow\left(2x-1\right)^2-\left(x+5\right)^2=0\Leftrightarrow\left(2x-1-x-5\right)\left(2x-1+x+5\right)=0\Leftrightarrow x=6;x=-\dfrac{4}{3}\)

Vậy tập nghiệm của phương trình là S = { -4/3 ; 6 } 

d, \(\left|3x+1\right|=x-2\)

TH1 : \(3x+1=x-2\Leftrightarrow2x=-3\Leftrightarrow x=-\dfrac{3}{2}\)

TH2 : \(3x+1=-x+2\Leftrightarrow4x=1\Leftrightarrow x=\dfrac{1}{4}\)

Vậy tập nghiệm của phương trình là S = { -3/2 ; 1/4 } 

các ý còn lại tương tự 

a) Ta có: \(\left(x^2-5x+7\right)^2-\left(2x-5\right)^2=0\)

\(\Leftrightarrow\left(x^2-5x+7-2x+5\right)\left(x^2-5x+7+2x-5\right)=0\)

\(\Leftrightarrow\left(x^2-7x+12\right)\left(x^2-3x+2\right)=0\)

\(\Leftrightarrow\left(x-3\right)\left(x-4\right)\left(x-1\right)\left(x-2\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x-3=0\\x-4=0\\x-1=0\\x-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=4\\x=1\\x=2\end{matrix}\right.\)

Vậy: S={3;4;1;2}

b) Ta có: |2x-1|=5

\(\Leftrightarrow\left[{}\begin{matrix}2x-1=5\\2x-1=-5\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=6\\2x=-4\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=3\\x=-2\end{matrix}\right.\)

Vậy: S={3;-2}