Trong các khoảng thời gian từ 0 đến \(\dfrac{T}{4}\), từ \(\dfrac{T}{4}\) đến \(\dfrac{T}{2}\), từ \(\dfrac{T}{2}\) đến \(\dfrac{3T}{4}\), từ \(\dfrac{3T}{4}\) đến \(T\), gia tốc của dao động thay đổi như thế nào?

Những câu hỏi liên quan
Trong các khoảng thời gian từ 0 đến \(\dfrac{T}{4}\), từ \(\dfrac{T}{4}\) đến \(\dfrac{T}{2}\), từ \(\dfrac{T}{2}\) đến \(\dfrac{3T}{4}\), từ \(\dfrac{3T}{4}\) đến \(T\), vận tốc của dao động điều hoà thay đổi như thế nào?
Trong các khoảng thời gian từ 0 đến \(\dfrac{T}{4}\) , từ \(\dfrac{T}{4}\) đến , \(\dfrac{T}{2}\) từ \(\dfrac{T}{2}\) đến \(\dfrac{3T}{4}\) , \(\dfrac{3T}{4}\) từ đến T vận tốc của dao động điều hoà thay đổi:
Từ 0 đến \(\dfrac{T}{4}\): vận tốc có hướng từ biên về vị trí cân bằng ngược chiều dương, độ lớn tăng dần từ 0 và đạt giá trị lớn nhất tại \(\dfrac{T}{4}\)
Từ \(\dfrac{T}{4}\) đến \(\dfrac{T}{2}\): vận tốc có hướng từ vị trí cân bằng về biên ngược với chiều dương, độ lớn giảm dần từ giá trị lớn nhất về 0 tại \(\dfrac{T}{2}\)
Từ \(\dfrac{T}{2}\) đến \(\dfrac{3T}{4}\): vận tốc có hướng từ vị trí biên về vị trí cân bằng cùng chiều dương, độ lớn tăng dần từ 0 và đạt giá trị lớn nhất tại \(\dfrac{3T}{4}\)
Từ \(\dfrac{3T}{4}\) đến T: vận tốc có hướng từ vị trí cân bằng về biên cùng chiều dương, độ lớn giảm dần từ giá trị lớn nhất về 0 tại T.
Đúng 0
Bình luận (0)
Hình 5.4 là đồ thị động năng và thế năng của một vật dao động điều hòa theo thời gian.a) Động năng và thế năng của vật thay đổi như thế nào trong các khoảng thời gian: từ 0 đến dfrac{T}{4}, từ dfrac{T}{4} đến dfrac{T}{2}, từ dfrac{T}{2} đến dfrac{3T}{4}, từ dfrac{3T}{4} đến T.b) Tại các thời điểm: t 0; tdfrac{T}{8};tdfrac{T}{4};tdfrac{3T}{4}, động năng và thế năng của vật có giá trị như thế nào (tính theo W). Nghiệm lại để thấy ở mỗi thời điểm đó Wđ + Wt W.
Đọc tiếp
Hình 5.4 là đồ thị động năng và thế năng của một vật dao động điều hòa theo thời gian.
a) Động năng và thế năng của vật thay đổi như thế nào trong các khoảng thời gian: từ 0 đến \(\dfrac{T}{4}\), từ \(\dfrac{T}{4}\) đến \(\dfrac{T}{2}\), từ \(\dfrac{T}{2}\) đến \(\dfrac{3T}{4}\), từ \(\dfrac{3T}{4}\) đến T.
b) Tại các thời điểm: t = 0; \(t=\dfrac{T}{8};t=\dfrac{T}{4};t=\dfrac{3T}{4}\), động năng và thế năng của vật có giá trị như thế nào (tính theo W). Nghiệm lại để thấy ở mỗi thời điểm đó Wđ + Wt = W.
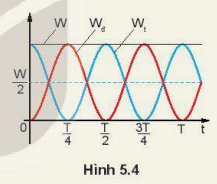
a) Từ 0 đến \(\frac{T}{4}\): Wđ tăng từ 0 đến giá trị lớn nhất tại \(\frac{T}{4}\), Wt giảm từ giá trị lớn nhất về 0 tại \(\frac{T}{4}\).
Từ \(\frac{T}{4}\)đến \(\frac{T}{2}\): Wđ giảm từ giá trị lớn nhất về 0 tại \(\frac{T}{2}\), Wt tăng từ 0 đến giá trị lớn nhất tại \(\frac{T}{2}\).
Từ \(\frac{T}{2}\)đến \(\frac{{3T}}{4}\): Wđ tăng từ 0 đạt giá trị lớn nhất tại \(\frac{{3T}}{4}\),Wt giảm từ giá trị lớn nhất về 0 tại \(\frac{{3T}}{4}\).
Từ \(\frac{{3T}}{4}\)đến T: Wđ giảm từ giá trị lớn nhất về 0 tại T, Wt tăng từ 0 đến giá trị lớn nhất tại T.
b) Tại thời điểm t = 0: Wđ = 0, Wt = W.
Tại thời điểm t = \(\frac{T}{8}\): Wđ = Wt = \(\frac{{\rm{W}}}{2}\).
Tại thời điểm t = \(\frac{T}{4}\): Wđ = W, Wt = 0.
Tại thời điểm t = \(\frac{{3T}}{8}\): Wđ = Wt = \(\frac{{\rm{W}}}{2}\).
→ ở mỗi thời điểm trên ta đều có: Wđ + Wt = W.
Đúng 0
Bình luận (0)
Một chất điểm dao động điều hoà với chu kì T= 0,2s,biên độ A= 4 cm. Tính tốc độ trung bình của vật trong khoảng thời gian ngắn nhất khi đi từ vị trí có li độ x= A đến vị trí có li độ x= \(-\dfrac{A}{2}\)
Để tính tốc độ trung bình của vật trong khoảng thời gian ngắn nhất khi đi từ vị trí có li độ x = A đến vị trí có li độ x = -A^2 - √2, ta cần biết hàm li độ của chất điểm dao động điều hoà.
Hàm li độ của chất điểm dao động điều hoà có thể được biểu diễn như sau: x(t) = A*cos(2πt/T)
Trong đó:
x(t) là li độ của chất điểm tại thời điểm tA là biên độ của dao độngT là chu kì của dao độngĐể tính tốc độ trung bình, ta sử dụng công thức: v(trung bình) = Δx/Δt
Trong trường hợp này, Δx là sự thay đổi li độ từ x = A đến x = -A^2 - √2, và Δt là khoảng thời gian tương ứng.
Δx = (-A^2 - √2) - A = -A^2 - √2 - A Δt = khoảng thời gian từ x = A đến x = -A^2 - √2 = T/4
Vậy, tốc độ trung bình của vật trong khoảng thời gian ngắn nhất là: v(trung bình) = Δx/Δt = (-A^2 - √2 - A) / (T/4)
Đúng 0
Bình luận (0)
Aật dao động điều hòa với biên độ A và chu kì T . Khoảng thời gian ngắn nhất vật đi từ li độ x = \(\dfrac{-A\sqrt{2}}{2}\) đến li độ x = \(\dfrac{A\sqrt{3}}{2}\) là
Để tmin => vật phải đi qua vị trí cân bằng:
\(x_1=\dfrac{-A\sqrt{2}}{2}\rightarrow x_2=\dfrac{A\sqrt{3}}{2}\) => t=\(\dfrac{7T}{24}\) (vtlg)
Đúng 1
Bình luận (0)
Quảng đường AB dài 76m,người thứ nhất đi từ A đến B và người thứ hai đi từ B đến A. vận tốc nguòi thứ nhất bằng dfrac{4}{5} vận tốc của người thứ hai.Đến lúc gặp nhau thời gian của người thứ nhất chỉ bằng dfrac{10}{11} thời gian của người thứ hai.Tính quãng đường mỗi người đi được.
Toán thục tế nha mọi người.Giúp mình với mọi người mình cần gấp.
Đọc tiếp
Quảng đường AB dài 76m,người thứ nhất đi từ A đến B và người thứ hai đi từ B đến A. vận tốc nguòi thứ nhất bằng \(\dfrac{4}{5}\) vận tốc của người thứ hai.Đến lúc gặp nhau thời gian của người thứ nhất chỉ bằng \(\dfrac{10}{11}\) thời gian của người thứ hai.Tính quãng đường mỗi người đi được.
Toán thục tế nha mọi người.Giúp mình với mọi người mình cần gấp.
một chất điểm dao động điều hoà với chu kì T,A4. trong khoảng thời gian ngắn nhất khi đó đi từ vị trí biên có li độ A đến vị trí x-Asqrt{2} ,chất điểm có tốc độ trung bình là
A.dfrac{6A}{T}
B. dfrac{4,5A}{T}
C. dfrac{1,5A}{T}
D.dfrac{4A}{T}
Đọc tiếp
một chất điểm dao động điều hoà với chu kì T,A=4. trong khoảng thời gian ngắn nhất khi đó đi từ vị trí biên có li độ A đến vị trí x=-A\(\sqrt{2}\) ,chất điểm có tốc độ trung bình là
A.\(\dfrac{6A}{T}\)
B. \(\dfrac{4,5A}{T}\)
C. \(\dfrac{1,5A}{T}\)
D.\(\dfrac{4A}{T}\)
Một ô tô chuyển động từ A đến B. Đoạn đầu ô tô đi mất dfrac{1}{4} tổng thời gian với vận tốc 40km/h. Đoạn giữa ô tô đi mất dfrac{1}{2} tổng thời gian với vận tốc 20m/s . Đoạn cuối ô tô đi mất dfrac{1}{4} tổng thời gian với vận tốc là 30km/h. Tính vận tốc trung bình của ô tô trên cả quãng đường.
Đọc tiếp
Một ô tô chuyển động từ A đến B. Đoạn đầu ô tô đi mất \(\dfrac{1}{4}\) tổng thời gian với vận tốc 40km/h. Đoạn giữa ô tô đi mất \(\dfrac{1}{2}\) tổng thời gian với vận tốc 20m/s . Đoạn cuối ô tô đi mất \(\dfrac{1}{4}\) tổng thời gian với vận tốc là 30km/h. Tính vận tốc trung bình của ô tô trên cả quãng đường.
GIẢI :
Đổi : 20m/s = 72km/h
Gọi t (h) là tổng thời gian ô tô chuyển động từ A đến B.
Quãng đường ô tô đi trong đoạn đầu mất 1/4 tổng thời gian là :
\(s_1=v_1.t_1=40.\dfrac{1}{4}t=10t\left(km\right)\)
Quãng đường ô tô đi trong đoạn giữa mất 1/2 tổng thời gian là :
\(s_2=v_2.t_2=72.\dfrac{1}{2}t=36t\left(km\right)\)
Quãng đường ô tô đi trong đoạn cuối mất 1/4 tổng thời gian là :
\(s_3=v_3.t_3=30.\dfrac{1}{4}t=7,5t\left(km\right)\)
Vận tốc trung bình của ô tô tren cả quãng đường là :
\(v_{tb}=\dfrac{s_1+s_2+s_3}{t_1+t_2+t_3}=\dfrac{10t+36t+7,5t}{\dfrac{t}{4}+\dfrac{t}{2}+\dfrac{t}{4}}=\dfrac{53,5t}{t}=53,5\left(km/h\right)\)
Vậy vận tốc trung bình của ô tô tren cả quãng đường là 53,5km/h
Đúng 0
Bình luận (0)
Đổi: \(20m\)/\(s\) \(=72km\)/\(h\)
Vận tốc trung bình của ô tô trên cả quãng đường là:
\(V_{tb}=\dfrac{S_1+S_2+S_3}{t_1+t_2+t_3}=\dfrac{V_1.t_1+V_2.t_2+V_3.t_3}{t_1+t_2+t_3}\)
\(=\dfrac{\left(40.\dfrac{1}{4}.t_1\right)+\left(72.\dfrac{1}{2}.t_2\right)+\left(30.\dfrac{1}{4}.t_3\right)}{t}\)
\(=\dfrac{\left(10+36+7,5\right)\left(t_1+t_2+t_3\right)}{t}=50,5\left(km\right)\)
Vậy ....
Đúng 0
Bình luận (10)
Một vật dao động có phương trình x = 5cos(4\(\pi\) + \(\dfrac{\pi}{3}\) )cm. Tốc độ trung bình của vật trong khoảng thời gian tính từ lúc t=0 đến thời điểm vật đi qua VTCB theo chiều dương lần thứ nhất bằng bao nhiêu?
Một vật dao động điều hòa theo phương trình x4cos(2Pi t + dfrac{Pi}{6} )
a) Sau bao lâu vật đi được quãng đường 22sqrt{3} kể từ t0
b) Tìm quãng đường lớn nhất và nhỏ nhất vật đi được trong thời gian dfrac{4}{3} s
c) Tìm tốc độ trung bình trong khoảng thời gian dfrac{11}{3} kể từ t 0
Đọc tiếp
Một vật dao động điều hòa theo phương trình x=4cos(\(2\Pi t\) + \(\dfrac{\Pi}{6}\) )
a) Sau bao lâu vật đi được quãng đường 22\(\sqrt{3}\) kể từ t=0
b) Tìm quãng đường lớn nhất và nhỏ nhất vật đi được trong thời gian \(\dfrac{4}{3}\) s
c) Tìm tốc độ trung bình trong khoảng thời gian \(\dfrac{11}{3}\) kể từ t =0
















