\(\dfrac{9^{15}.8^{11}}{3^{29}.16^8}=\dfrac{\left(3^2\right)^{15}.\left(2^3\right)^{11}}{3^{29}.\left(2^4\right)^8}=\dfrac{3^{30}.2^{33}}{3^{29}.2^{32}}\)

Ta lấy vễ trên chia vế dưới

\(=3.2=6\)

\(\dfrac{2^{11}.9^3}{3^5.16^2}=\dfrac{2^{11}.\left(3^2\right)^3}{3^5.\left(2^4\right)^2}=\dfrac{2^{11}.3^6}{3^5.2^8}\)

Ta lấy vế trên chia vế dưới

\(=2^3.3=24\)

\(\dfrac{9^{15}.8^{11}}{3^{29}.16^8}=\dfrac{\left(3^2\right)^{15}.\left(2^3\right)^{11}}{3^{29}.\left(2^4\right)^8}=\dfrac{3^{30}.2^{33}}{3^{29}.3^{32}}=3.2=6\)
\(\dfrac{2^{11}.9^3}{3^5.16^2}=\dfrac{2^{11}.\left(3^2\right)^3}{3^5.\left(2^4\right)^2}=\dfrac{2^{11}.3^6}{3^5.2^8}=2^3.3=8.3=24\)

\(\dfrac{9^{15}.8^{11}}{3^{29}.16^8}=\dfrac{3^{30}.2^{33}}{3^{29}.2^{32}}=3.2=6\)

\(\dfrac{2^{11}.9^3}{3^5.16^2}=\dfrac{2^{11}.3^6}{3^5.2^8}=2^3.3=8.3=24\)

working

directly

Working ( stop+V-ing)
Directly

tui chịu luôn đó

Câu 1 này bình phương hơi dài dòng nên khử trị tuyệt đối sẽ tốt hơn:

\(\left[{}\begin{matrix}\left\{{}\begin{matrix}x^2-2x-3\ge0\\x^2-2x-3\ge3x-3\end{matrix}\right.\\\left\{{}\begin{matrix}x^2-2x-3< 0\\-\left(x^2-2x-3\right)\ge3x-3\end{matrix}\right.\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}\left[{}\begin{matrix}x\ge3\\x\le-1\end{matrix}\right.\\x^2-5x\ge0\end{matrix}\right.\\\left\{{}\begin{matrix}-1< x< 3\\x^2+x-6\le0\end{matrix}\right.\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}\left[{}\begin{matrix}x\ge3\\x\le-1\end{matrix}\right.\\\left[{}\begin{matrix}x\ge5\\x\le0\end{matrix}\right.\end{matrix}\right.\\\left\{{}\begin{matrix}-1< x< 3\\-3\le x\le2\end{matrix}\right.\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x\ge5\\x\le-1\end{matrix}\right.\\-1< x\le2\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}x\ge5\\x\le2\end{matrix}\right.\)

Vậy C đúng

`81^8=3^x`

`=>3^x=(3^4)^8`

`=>3^x=3^32`

`=>x=32`

Vậy `x=32`

x=32

\(81^8=3^x\)

\(\Leftrightarrow\left(3^4\right)^8=3^x\)

\(\Leftrightarrow3^{32}=3^x\)

\(\Leftrightarrow x=32\)

Câu nào bạn, nếu mà cả thì đăng tách ra đi :)

1.

\(sin^2x-4sinx.cosx+3cos^2x=0\)

\(\Rightarrow\dfrac{sin^2x}{cos^2x}-\dfrac{4sinx}{cosx}+\dfrac{3cos^2x}{cos^2x}=0\)

\(\Rightarrow tan^2x-4tanx+3=0\)

2.

\(\Leftrightarrow\dfrac{1}{2}cos2x+\dfrac{\sqrt{3}}{2}sin2x=\dfrac{1}{2}\)

\(\Leftrightarrow cos\left(2x-\dfrac{\pi}{3}\right)=\dfrac{1}{2}\)

3.

\(\Leftrightarrow2^2+m^2\ge1\)

\(\Leftrightarrow m^2\ge-3\) (luôn đúng)

Pt có nghiệm với mọi m (đề bài sai)

4.

\(\Leftrightarrow\dfrac{1}{2}sinx-\dfrac{\sqrt{3}}{2}cosx=1\)

\(\Leftrightarrow sin\left(x-\dfrac{\pi}{3}\right)=1\)

\(\Leftrightarrow x-\dfrac{\pi}{3}=\dfrac{\pi}{2}+k2\pi\)

\(\Leftrightarrow x=\dfrac{5\pi}{6}+k2\pi\)

6.

ĐKXĐ: \(cosx\ne0\)

Nhân 2 vế với \(cos^2x\)

\(sin^2x-4cosx+5cos^2x=0\)

\(\Leftrightarrow1-cos^2x-4cosx+5cos^2x=0\)

\(\Leftrightarrow\left(2cosx-1\right)^2=0\)

\(\Leftrightarrow cosx=\dfrac{1}{2}\Rightarrow x=\pm\dfrac{\pi}{3}+k2\pi\)

6.

\(cos^2x+\sqrt{3}sinx.cosx-1=0\)

\(\Leftrightarrow-sin^2x+\sqrt{3}sinx.cosx=0\)

\(\Leftrightarrow sinx\left(sinx-\sqrt{3}cosx\right)=0\)

\(\Leftrightarrow sinx\left(\dfrac{1}{2}sinx-\dfrac{\sqrt{3}}{2}cosx\right)=0\)

\(\Leftrightarrow sinx.sin\left(x-\dfrac{\pi}{3}\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}sinx=0\\sin\left(x-\dfrac{\pi}{3}\right)=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=k\pi\\x=\dfrac{\pi}{3}+k\pi\end{matrix}\right.\)

7.

\(\sqrt{3}sinx-cosx=2\)

\(\Leftrightarrow\dfrac{\sqrt{3}}{2}sinx-\dfrac{1}{2}cosx=1\)

\(\Leftrightarrow sin\left(x-\dfrac{\pi}{3}\right)=1\)

\(\Leftrightarrow x-\dfrac{\pi}{3}=\dfrac{\pi}{2}+k2\pi\)

\(\Leftrightarrow x=\dfrac{5\pi}{6}+k2\pi\)

8.

\(sin4x+\sqrt{3}cos4x=2sinx\)

\(\Leftrightarrow\dfrac{1}{2}sin4x+\dfrac{\sqrt{3}}{2}cos4x=sinx\)

\(\Leftrightarrow sin\left(4x+\dfrac{\pi}{3}\right)=sinx\)

\(\Leftrightarrow\left[{}\begin{matrix}4x+\dfrac{\pi}{3}=x+k2\pi\\4x+\dfrac{\pi}{3}=\pi-x+k2\pi\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{9}+\dfrac{k2\pi}{3}\\x=\dfrac{2\pi}{15}+\dfrac{k2\pi}{5}\end{matrix}\right.\)

LÀ CON CHUỒN CHUỒN CÒN GÌ NỮA .

chuồn chuồn = chuồn + chuônf

12.

\(y=\sqrt{2}sin\left(2x+\dfrac{\pi}{4}\right)\le\sqrt[]{2}\)

\(\Rightarrow M=\sqrt{2}\)

13.

Pt có nghiệm khi:

\(5^2+m^2\ge\left(m+1\right)^2\)

\(\Leftrightarrow2m\le24\)

\(\Rightarrow m\le12\)

14.

\(\Leftrightarrow\left[{}\begin{matrix}cosx=1\\cosx=-\dfrac{5}{3}\left(loại\right)\end{matrix}\right.\)

\(\Leftrightarrow x=k2\pi\)

15.

\(\Leftrightarrow\left[{}\begin{matrix}tanx=-1\\tanx=3\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}x=-\dfrac{\pi}{4}+k\pi\\x=arctan\left(3\right)+k\pi\end{matrix}\right.\)

Đáp án A

16.

\(\dfrac{\sqrt{3}}{2}sinx-\dfrac{1}{2}cosx=\dfrac{1}{2}\)

\(\Leftrightarrow sin\left(x-\dfrac{\pi}{6}\right)=\dfrac{1}{2}\)

\(\Leftrightarrow\left[{}\begin{matrix}x-\dfrac{\pi}{6}=\dfrac{\pi}{6}+k2\pi\\x-\dfrac{\pi}{6}=\dfrac{5\pi}{6}+k2\pi\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{3}+k2\pi\\x=\pi+k2\pi\end{matrix}\right.\)

\(\left[{}\begin{matrix}2\pi\le\dfrac{\pi}{3}+k2\pi\le2018\pi\\2\pi\le\pi+k2\pi\le2018\pi\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}1\le k\le1008\\1\le k\le1008\end{matrix}\right.\)

Có \(1008+1008=2016\) nghiệm

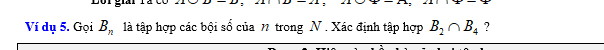
\(B_2=\left\{x;x=2k,k\in N\right\}\)

\(B_4=\left\{x;x=4m,m\in N\right\}\)

Do \(4m=2.\left(2m\right)\Rightarrow B_4\subset B_2\)

\(\Rightarrow B_2\cap B_4=B_4\)