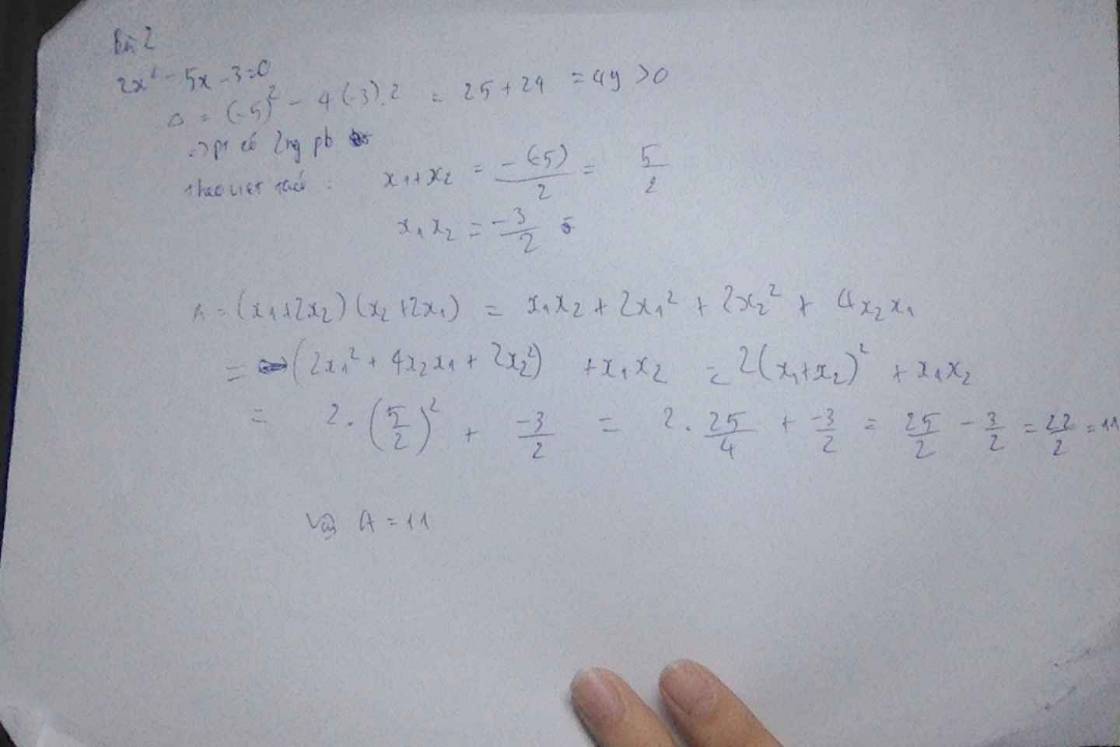\(\Delta'=\left[-\left(m+1\right)\right]^2-\left(m^2+m\right)=m^2+2m+1-m^2-m\)

\(=m+1\)

pt có nghiệm x1,x2 \(< =>m+1\ge0< =>m\ge-1\)

vi ét \(=>\left\{{}\begin{matrix}x1+x2=2m+2\\x1x2=m^2+m\end{matrix}\right.\)

a,\(=>2m+2=m^2+m< =>m^2-m-2=0\)

\(a-b+c=0=>\left[{}\begin{matrix}m1=-1\\m2=2\end{matrix}\right.\left(tm\right)\)

b,\(< =>3\left(2m+2\right)-2\left(m^2+m\right)-1=0\)

\(< =>-2m^2+4m+5=0\)

\(ac< 0\) pt có 2 nghiệm pbiet \(=>\left[{}\begin{matrix}m1=...\\m2=...\end{matrix}\right.\) thay số vào tính m1,m2 đối chiếu đk

1, Theo Vi-ét:\(\left\{{}\begin{matrix}x_1+x_2=-5\\x_1x_2=-6\end{matrix}\right.\)

\(A=\left(x_1-2x_2\right)\left(2x_1-x_2\right)\\ =2x_1^2-4x_1x_2-x_1x_2+2x_1^2\\ =2\left(x_1^2+x_2^2\right)-5x_1x_2\\ =2\left[\left(x_1+x_2\right)^2-2x_1x_2\right]-5x_1x_2\\ =2\left(-5\right)^2-4.\left(-6\right)-5.\left(-6\right)\\ =104\)

2, Theo Vi-ét:\(\left\{{}\begin{matrix}x_1+x_2=5\\x_1x_2=-3\end{matrix}\right.\)

\(B=x_1^3x_2+x_1x_2^3\\ =x_1x_2\left(x_1^2+x_2^2\right)\\ =\left(-3\right)\left[\left(x_1+x_2\right)^2-2x_1x_2\right]\\ =\left(-3\right)\left[5^2-2\left(-3\right)\right]\\ =-93\)

Chị cho e hệ thức Vi-ét của bài được hongg ạ?

\(x_1+x_2=2\left(m-1\right)\)( Vi-ét )

\(\rightarrow x_1+x_2=2m-2\)

\(\Leftrightarrow x_1-2m=-2-x_2\)

\(x_1^2-2mx_1=x_1\left(x_1-2m\right)=x_1\left(-2-x_2\right)=-2x_1-x_1x_2=-2x_1-\left(2m-5\right)=5-2m-2x_1\)

                   _ Phía sau tương tự với `x_2` nha chị uii_

Moij người giúp mình với ạ mình đang cần gấp ạ

\(\Delta'=9-6m+m^2=\left(m-3\right)^2\ge0;\forall m\)

\(\Rightarrow\) Pt luôn có nghiệm với mọi m

Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-6\\x_1x_2=6m-m^2\end{matrix}\right.\)

Do \(x_1\) là nghiệm nên: \(x_1^2+6x_1+6m-m^2=0\Leftrightarrow2x_1^2+12x_1=2m^2-12\)

\(x_1^3-x_2^3+2x_1^2+12x_1+72=0\)

\(\Leftrightarrow\left(x_1-x_2\right)\left[\left(x_1+x_2\right)^2-x_1x_2\right]+2m^2-12m+72=0\)

\(\Leftrightarrow\left(x_1-x_2\right)\left(m^2-6m+36\right)+2m^2-12m+72=0\)

\(\Leftrightarrow\left(x_1-x_2+2\right)\left(m^2-6m+36\right)=0\)

\(\Leftrightarrow x_1-x_2+2=0\) (do \(m^2-6m+36=\left(m-3\right)^2+27>0;\forall m\))

Kết hợp với \(x_1+x_2=-6\) ta được: 

\(\left\{{}\begin{matrix}x_1-x_2=-2\\x_1+x_2=-6\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_1=-4\\x_2=-2\end{matrix}\right.\)

Thế vào \(x_1x_2=6m-m^2\)

\(\Rightarrow8=6m-m^2\Rightarrow m^2-6m+8=0\Rightarrow\left[{}\begin{matrix}m=2\\m=4\end{matrix}\right.\)

Theo hệ thức Viète ta có : \(\hept{\begin{cases}x_1+x_2=-\frac{b}{a}=\frac{5}{2}\\x_1x_2=\frac{c}{a}=-\frac{3}{2}\end{cases}}\)

Khi đó : A = ( x₁ + 2x₂ )( x₂ + 2x₁ ) = x₁x₂ + 2x₁² + 2x₂² + 4x₁x₂

= 5x₁x₂ + 2( x₁ + x₂ )² - 4x₁x₂

= 2( x₁ + x₂ )² + x₁x₂ = 2.(5/2)² - 3/2 = 11

A=11