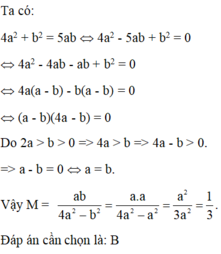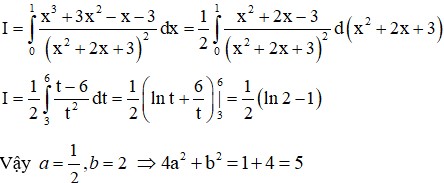Ta có:

\(4a^2+b^2=5ab\Leftrightarrow4a^2+b^2-4ab-ab=0\)

\(\Leftrightarrow4a\left(a-b\right)-b\left(a-b\right)=0\)

\(\Leftrightarrow\left(a-b\right)\left(4a-b\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}a-b=0\\4a-b=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}a=b\left(ktm\right)\\4a=b\left(tm\right)\end{matrix}\right.\)

\(\Rightarrow4a=b\)

\(\Rightarrow\dfrac{5ab}{3a^2+2b^2}=\dfrac{5a.4a}{3a^2+2.\left(4a\right)^2}=\dfrac{20a^2}{3a^2+32a^2}\)

\(=\dfrac{20a^2}{35a^2}=\dfrac{4}{7}\)

\(4a^2+b^2=5ab\)

\(\Rightarrow4a\left(a-b\right)-b\left(a-b\right)=0\)

\(\Rightarrow\left(a-b\right)\left(4a-b\right)=0\)

\(\Rightarrow b=4a\left(do.a\ne b\right)\)

\(\dfrac{5ab}{3a^2+2b^2}=\dfrac{20a^2}{3a^2+32a^2}=\dfrac{4}{7}\)

Lời giải:

$P=4a^2+b^2+c^2+4ab+4ac+2bc=(2a+b+c)^2=(-1)^2=1$

\(\Leftrightarrow4a^2+12ab+9b^2=10b^2\)

\(\Leftrightarrow\left[{}\begin{matrix}2a+3b=b\sqrt{10}\\2a+3b=-b\sqrt{10}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}a=\dfrac{b\sqrt{10}-3b}{2}\\a=\dfrac{-b\sqrt{10}-3b}{2}\end{matrix}\right.\)

Em kiểm tra lại đề bài

\(4a^2+b^2+3c^2=4ab\Leftrightarrow\left(2a-b\right)^2+3c^2=0\)

\(\Leftrightarrow\left\{{}\begin{matrix}2a-b=0\\c=0\end{matrix}\right.\)

Dẫn tới biểu thức P không xác định

Đáp án C

a,\(5ab-45a^3b\)

=\(5ab\left(1-9a^2\right)\)

=\(5ab\left(1-3a\right)\left(1+3a\right)\)

b,\(3a-6ab+5-10b\)

=\(\left(3a-6ab\right)+\left(5-10b\right)\)

=\(3a\left(1-2b\right)+5\left(1-2b\right)\)

=\(\left(1-2b\right)\left(3a+5\right)\)

c,\(a^2-7ab-2a+14b\)

=\(\left(a^2-7ab\right)-\left(2a-14b\right)\)

=\(a\left(a-7b\right)-2\left(a-7b\right)\)

=\(\left(a-7b\right)\left(a-2\right)\)

d,\(4a^2-8b+4a-8ab\)

=\(\left(4a^2-8ab\right)+\left(4a-8b\right)\)

=\(4a\left(a-2b\right)+4\left(a-2b\right)\)

=\(\left(a-2b\right)\left(4a+4\right)\)

=\(4\left(a-2b\right)\left(a+1\right)\)

e,\(a^2-5a+15b-9b^2\)

=\(\left(a^2-9b^2\right)-\left(5a-15b\right)\)

=\(\left(a-3b\right)\left(a+3b\right)-5\left(a-3b\right)\)

=\(\left(a-3b\right)\left(a+3b-5\right)\)