Câu 2. Cho đường thẳng $d:3x-2y+1=0$ và điểm $M\left( 1;2 \right)$. Viết phương trình đường thẳng $\Delta $ qua $M$ và tạo với $d$ một góc $45^{\circ}$.

Những câu hỏi liên quan
1. Cho đường tròn (c) : x^2+y^2+6x-2y0 và đường thẳng d : x-3y-40Tính tiếp tuyến của (C) song song với (d) 2. Tìm giá trị của m để đường thẳng Delta:3x+4y+30 tiếp xúc với (C) : left(x-mright)^2+y^293. Xác đinh m để left(C_mright):x^2+y^2-4x+2left(m+1right)y+3m+70 là phương trình của một đường tròn
Đọc tiếp
1. Cho đường tròn (c) : \(x^2+y^2+6x-2y=0\) và đường thẳng d : \(x-3y-4=0\)
Tính tiếp tuyến của (C) song song với (d)
2. Tìm giá trị của m để đường thẳng \(\Delta:3x+4y+3=0\) tiếp xúc với (C) : \(\left(x-m\right)^2+y^2=9\)
3. Xác đinh m để \(\left(C_m\right):x^2+y^2-4x+2\left(m+1\right)y+3m+7=0\) là phương trình của một đường tròn
1: x^2+y^2+6x-2y=0
=>x^2+6x+9+y^2-2y+1=10
=>(x+3)^2+(y-1)^2=10
=>R=căn 10; I(-3;1)
Vì (d1)//(d) nên (d1): x-3y+c=0
Theo đề, ta có: d(I;(d1))=căn 10
=>\(\dfrac{\left|-3\cdot1+1\cdot\left(-3\right)+c\right|}{\sqrt{1^2+\left(-3\right)^2}}=\sqrt{10}\)
=>|c-6|=10
=>c=16 hoặc c=-4
Đúng 0
Bình luận (0)
Câu 1: Giải phương trình và hệ phương trìnha) sqrt{4x^2-4x+9}3b) left{{}begin{matrix}3x-y52y-x0end{matrix}right.Câu 2:a) Cho hai đường thẳng (d_1): y 2x - 5 và (d_2): y 4x - m (m là tham số). Tìm tất cả các giá trị của tham số m để (d_1) và (d_2) cắt nhau tại một điểm trên trục hoành Oxb) Rút gọn biểu thức: Pleft(dfrac{sqrt{x}}{3+sqrt{x}}+dfrac{2x}{9-x}right):left(dfrac{sqrt{x}-1}{x-3sqrt{x}}-dfrac{2}{sqrt{x}}right) với x 0, x ne 9, x ne 25
Đọc tiếp
Câu 1: Giải phương trình và hệ phương trình
a) \(\sqrt{4x^2-4x+9}=3\)
b) \(\left\{{}\begin{matrix}3x-y=5\\2y-x=0\end{matrix}\right.\)
Câu 2:
a) Cho hai đường thẳng (d\(_1\)): y = 2x - 5 và (d\(_2\)): y = 4x - m (m là tham số). Tìm tất cả các giá trị của tham số m để (d\(_1\)) và (d\(_2\)) cắt nhau tại một điểm trên trục hoành Ox
b) Rút gọn biểu thức: \(P=\left(\dfrac{\sqrt{x}}{3+\sqrt{x}}+\dfrac{2x}{9-x}\right):\left(\dfrac{\sqrt{x}-1}{x-3\sqrt{x}}-\dfrac{2}{\sqrt{x}}\right)\) với x > 0, x \(\ne\) 9, x \(\ne\) 25
a) \(\sqrt{4x^2-4x+9}=3\)
Vì \(4x^2-4x+9=\left(2x-1\right)^2+8>0\)( Với mọi x )
Nên \(\sqrt{4x^2-4x+9}=3\)
⇔\(4x^2-4x+9=9\)
⇔\(4x^2-4x=0\)
⇔\(4x\left(x-1\right)=0\)
⇔\(\left[{}\begin{matrix}4x=0\\x-1=0\end{matrix}\right.\)
⇔\(\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)
Vậy \(\left[{}\begin{matrix}x=0\\x=1\end{matrix}\right.\)là nghiệm
Đúng 2
Bình luận (0)
Câu 1: Giải phương trình và hệ phương trình sau:a) x^4+3x^2-40b) left{{}begin{matrix}x+2y5x-5y-9end{matrix}right.Câu 2: Trên mặt phẳng tọa độ Oxy cho điểm T (-2; -2), (P) có phương trình y-8x^2 và đường thẳng d có phương trình y - 2x - 6a) Điểm T có thuộc đường thẳng d không ?b) Xác định tọa độ giao điểm của đường thẳng d và (P)
Đọc tiếp
Câu 1: Giải phương trình và hệ phương trình sau:
a) \(x^4+3x^2-4=0\)
b) \(\left\{{}\begin{matrix}x+2y=5\\x-5y=-9\end{matrix}\right.\)
Câu 2: Trên mặt phẳng tọa độ Oxy cho điểm T (-2; -2), (P) có phương trình \(y=-8x^2\) và đường thẳng d có phương trình y = - 2x - 6
a) Điểm T có thuộc đường thẳng d không ?
b) Xác định tọa độ giao điểm của đường thẳng d và (P)
Câu 1:
a) Ta có: \(x^4+3x^2-4=0\)
\(\Leftrightarrow x^4+4x^2-x^2-4=0\)
\(\Leftrightarrow x^2\left(x^2+4\right)-\left(x^2+4\right)=0\)
\(\Leftrightarrow\left(x^2+4\right)\left(x^2-1\right)=0\)
mà \(x^2+4>0\forall x\)
nên \(x^2-1=0\)
\(\Leftrightarrow x^2=1\)
hay \(x\in\left\{1;-1\right\}\)
Vậy: S={1;-1}
Đúng 0
Bình luận (0)
Câu 1:
b) Ta có: \(\left\{{}\begin{matrix}x+2y=5\\x-5y=-9\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}7y=14\\x+2y=5\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}y=2\\x=5-2y=1\end{matrix}\right.\)
Vậy: (x,y)=(1;2)
Đúng 0
Bình luận (0)
Câu 2:
a) Thay x=-2 vào (d), ta được:
\(y=-2\cdot\left(-2\right)-6=4-6=-2\)
Vậy: T(-2;-2) thuộc (d)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Giao điểm M của đường thẳng
d
:
x
1
-
2
t
y
-
3...
Đọc tiếp
Giao điểm M của đường thẳng d : x = 1 - 2 t y = - 3 + 5 t ( t ∈ ℝ ) và đường thẳng d’: 3x-2y -1= 0 là
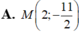
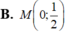
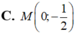
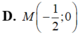
Thế 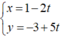 vào phương trình của d’ ta được:
vào phương trình của d’ ta được:
3( 1-2t) -2( -3+5t) -1 =0 hay -16t + 8= 0
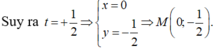
Chọn C.
Đúng 0
Bình luận (0)
Trong không gian Oxyz, cho bốn điểm A(0;0;1), B(1;2;4), C(1;0;1) và D(2;1;2). Gọi (P) là mặt phẳng qua C,D và song song với đường thẳng AB. Phương trình của (P) là:
A. x - 2y + z - 2 = 0.
B. 3x - 2y - z - 2 = 0.
C. 3x - z - 2 = 0.
D. 3x - 2y - z - 1 = 0.
\(\overrightarrow{AB}=\left(1;2;3\right)\) ; \(\overrightarrow{CD}=\left(1;1;1\right)\)
\(\left[\overrightarrow{AB};\overrightarrow{CD}\right]=\left(-1;2;-1\right)=-\left(1;-2;1\right)\)
Phương trình (P):
\(1\left(x-1\right)-2y+1\left(z-1\right)=0\Leftrightarrow x-2y+z-2=0\)
Đúng 1
Bình luận (0)
Để tìm phương trình mặt phẳng (P) ta cần tìm được vector pháp tuyến của mặt phẳng. Vì mặt phẳng (P) song song với đường thẳng AB nên vector pháp tuyến của (P) cũng vuông góc với vector chỉ phương của AB, tức là AB(1-0;2-0;4-1)=(1;2;3).
Vì (P) đi qua C(1;0;1) nên ta dễ dàng tìm được phương trình của (P) bằng cách sử dụng công thức phương trình mặt phẳng:
3x - 2y - z + d = 0, trong đó d là vế tự do.
Để tìm d, ta chỉ cần thay vào phương trình trên cặp tọa độ (x;y;z) của điểm C(1;0;1):
3(1) -2(0) - (1) + d = 0
⇒ d = -2
Vậy phương trình của mặt phẳng (P) là:
3x - 2y - z - 2 = 0,
và đáp án là B.
Đúng 0
Bình luận (0)
→AB=(1;2;3)��→=(1;2;3) ; −−→CD=(1;1;1)��→=(1;1;1)
[−−→AB;−−→CD]=(−1;2;−1)=−(1;−2;1)[��→;��→]=(−1;2;−1)=−(1;−2;1)
Phương trình (P):
1(x−1)−2y+1(z−1)=0⇔x−2y+z−2=0
Đúng 0
Bình luận (0)
Cho 2 đường thẳng (d1) y=3x + 4 và (d2) x - 2y =0 một điểm A ( -1; 1)
a xét vị trí tương đối của A với 2 đường thẳng
b tìm giao điểm (d1) và ( d2)
c tìm m để (d3) : ( m-1)x + (m-2)y + m +1=0 đồng quy với (d1) và (d2)
a) Thay hoành độ và tung độ của A vào 2 pt đường thẳng (d1) và (d2), ta lần lượt được:
\(1=3\left(-1\right)+4\) (luôn đúng)
\(-1-2.1=0\) (vô lí)
Như vậy, \(A\in d_1;A\notin d_2\)
b) Gọi giao điểm của d1, d2 là \(B\left(x_0;y_0\right)\). Khi đó \(x_0,y_0\) là các số thỏa mãn \(\left\{{}\begin{matrix}y_0=3x_0+4\\x_0-2y_0=0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}y_0=6y_0+4\\x_0=2y_0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}y_0=-\dfrac{4}{5}\\x_0=-\dfrac{8}{5}\end{matrix}\right.\)
Vậy giao điểm của d1 và d2 là \(B\left(-\dfrac{8}{5};-\dfrac{4}{5}\right)\)
c) Để đường thẳng d1, d2, d3 đồng quy thì d3 phải đi qua giao điểm của d1 và d2. Nói cách khác, d3 phải đi qua điểm \(B\left(-\dfrac{8}{5};-\dfrac{4}{5}\right)\)
\(\Leftrightarrow\left(m-1\right).\dfrac{-8}{5}+\left(m-2\right).\dfrac{-4}{5}+m+1=0\)
\(\Leftrightarrow\dfrac{21}{5}-\dfrac{7}{5}m=0\)
\(\Leftrightarrow m=3\)
Vậy \(m=3\) thỏa mãn ycbt.
Đúng 1
Bình luận (0)
cho điểm A(-1:3) và đường thẳng d : 4x-3y+8=0.Tìm điểm M trên đường thẳng \(\left(\Delta\right)\) : -x+2y+1=0 sao cho AM song song với đường thẳng d
M ∈ Δ => M( 1 + 2m ; m)
Do AM // d nên \(\overrightarrow{n_{AM}}=\overrightarrow{n_d}=\left(4;-3\right)\)
Phương trình AM có dạng: 4(x -1 - 2m) - 3(y - m) = 0
Mà A ∈ AM nên: 4(-1 -1 - 2m) - 3(3 - m) = 0
⇔ m= \(\frac{-17}{5}\) => M(\(\frac{-29}{5};\frac{-17}{5}\))
Đúng 0
Bình luận (0)
Cho hai điểm \(A\left(3;-1\right);B\left(-1;-2\right)\) và đường thẳng d có phương trình \(x+2y+1=0\)
a) Tìm tọa độ điểm C trên đường thẳng d sao cho tam giác ABC là tam giác cân tại C
b) Tìm tọa độ của điểm M trên đường thẳng d sao cho tam giác AMB vuông tại M
a) đặc C (x;y) , ta có : C \(\in\) (d) \(\Leftrightarrow x=-2y-1\)
vậy C (-2y -1 ; y ).
tam giác ABC cân tại C khi và chỉ khi
CA = CB \(\Leftrightarrow\) CA2 = CB2
\(\Leftrightarrow\) (3+ 2y + 1)2 + (- 1- y)2 = (- 1+ 2y + 1)2 + (- 2- y)2
\(\Leftrightarrow\) (4 + 2y)2 + (1 + y)2 = 4y2 + (2 + y)2
giải ra ta được y = \(\dfrac{-13}{14}\) ; x = \(-2\left(\dfrac{-13}{14}\right)-1=\dfrac{13}{7}-1=\dfrac{6}{7}\)
vậy C có tọa độ là \(\left(\dfrac{6}{7};\dfrac{-13}{14}\right)\)
b) xét điểm M (- 2t - 1 ; t) trên (d) , ta có :
\(\widehat{AMB}\) = 900 \(\Leftrightarrow\) AM2 + BM2 = AB2
\(\Leftrightarrow\) (4 + 2t)2 + (1 + t)2 + 4t2 + (2 + t)2 = 17
\(\Leftrightarrow\) 10t2 +22t + 4 = 0 \(\Leftrightarrow\) 5t2 + 11t + 2 = 0
\(\Leftrightarrow\left\{{}\begin{matrix}t=\dfrac{-1}{5}\\t=-2\end{matrix}\right.\)
vậy có 2 điểm thỏa mãn đề bài là M1\(\left(\dfrac{-3}{5};\dfrac{-1}{5}\right)\) và M2\(\left(3;-2\right)\)
Đúng 0
Bình luận (0)
1. Cho đường thẳng $(d):$ $y = ax+b$. Tìm $a$ và $b$ để đường thẳng $(d)$ song song với đường thẳng $(d'):$ $y = 5x+6$ và đi qua điểm $A(2;3)$.
2. Giải hệ phương trình $\left\{ \begin{aligned} & 3x + 2y = 11\\ & x + 2y = 5\\ \end{aligned}\right.$.
Bài 2 :
\(\hept{\begin{cases}3x+2y=11\left(1\right)\\x+2y=5\left(2\right)\end{cases}}\)
Lấy phương trình (1) - phương trình (2) ta được :
\(2x=6\Leftrightarrow x=3\)
Thay x = 3 vào phương trình (2) ta được :
\(3+2y=5\Leftrightarrow2y=2\Leftrightarrow y=1\)
Vậy \(\left(x;y\right)=\left(3;1\right)\)
1 , a = 5 , b = -7
2 , x = 3 , y = 1

























