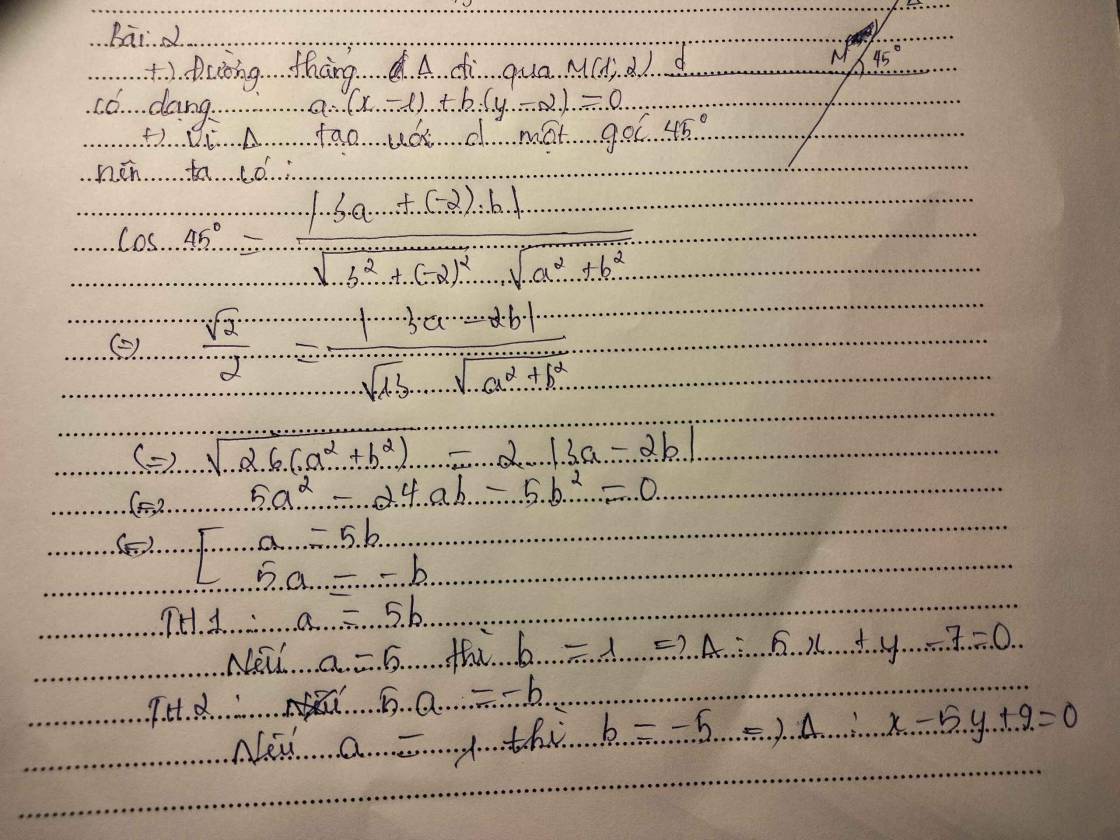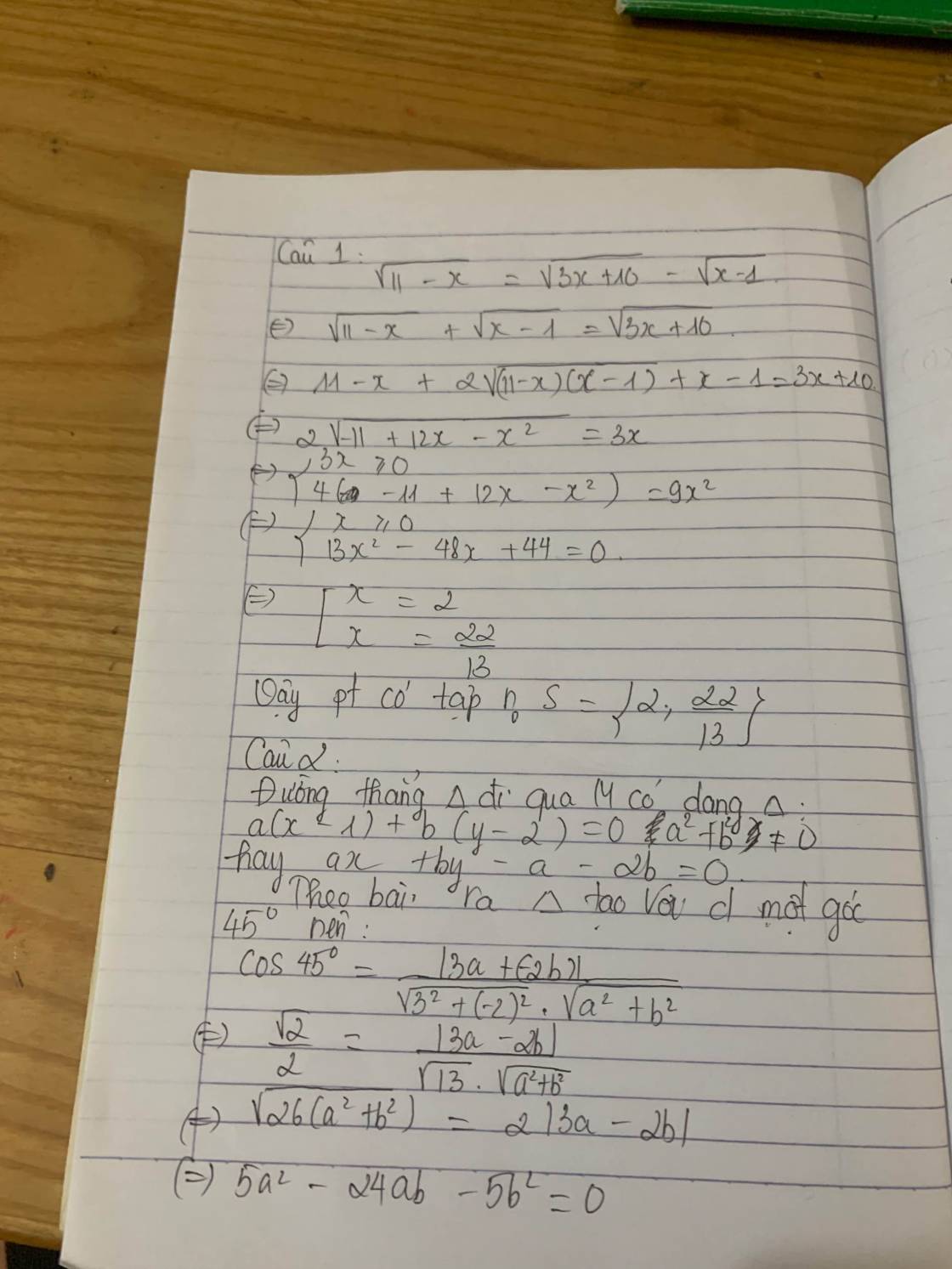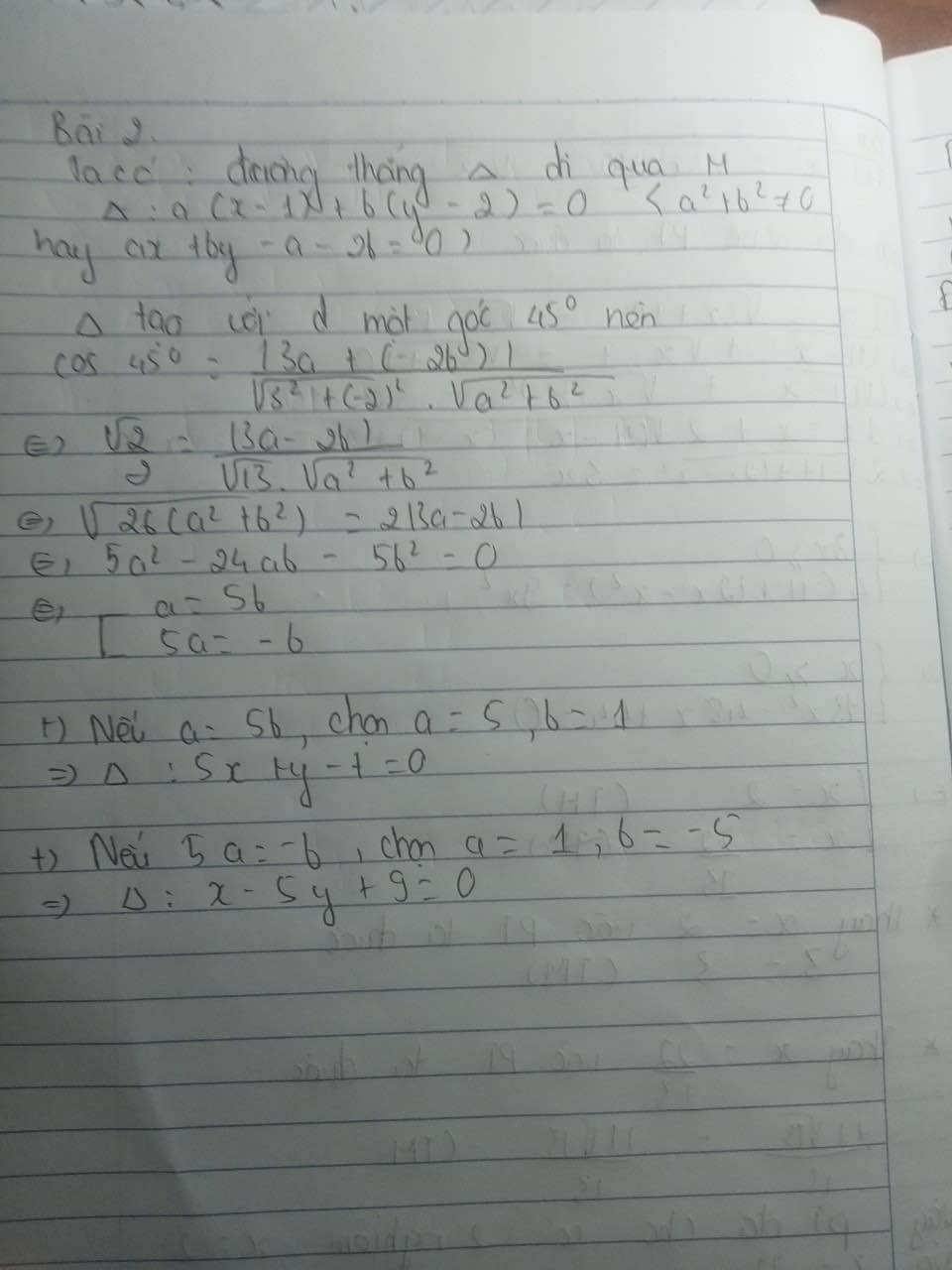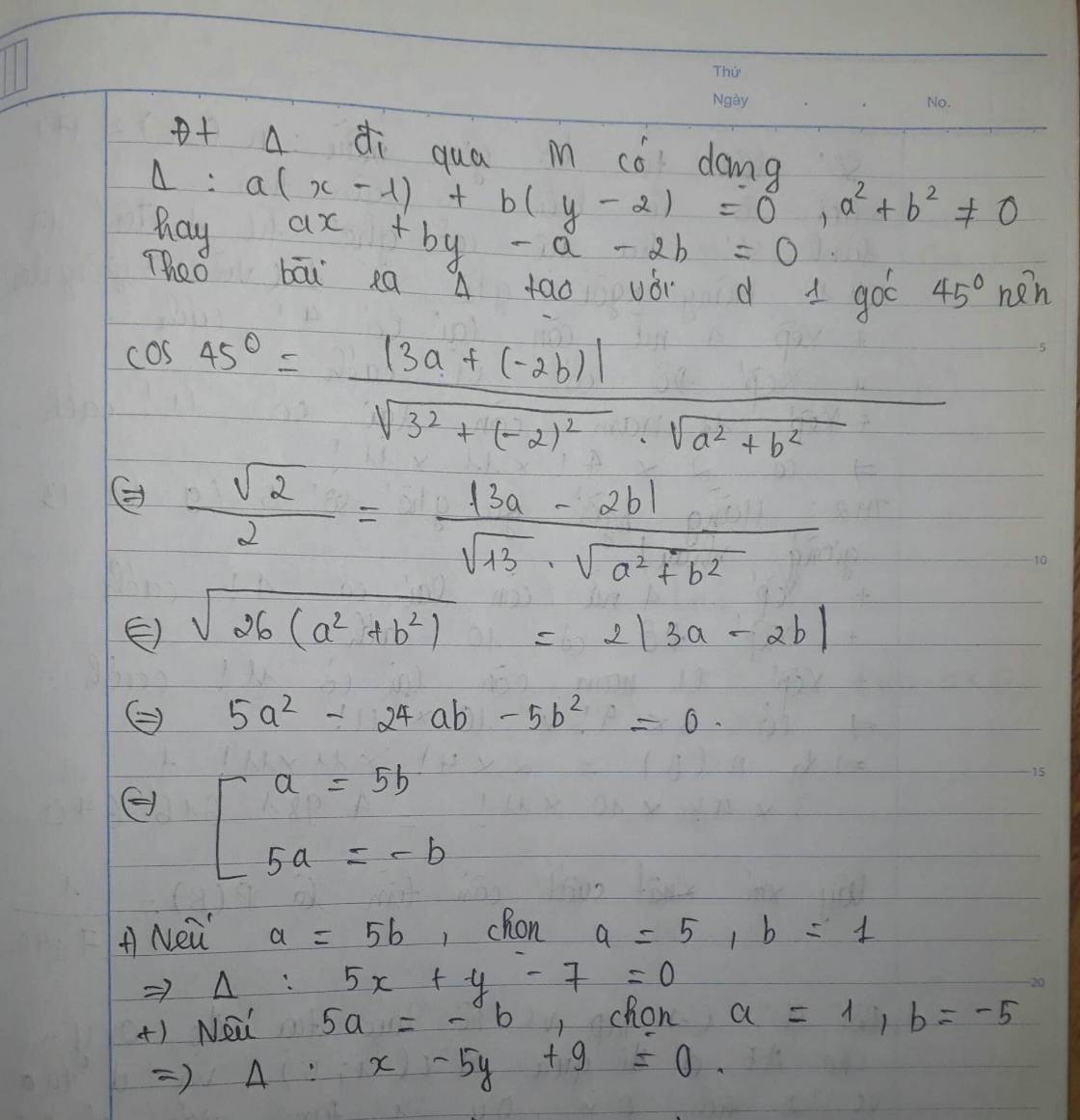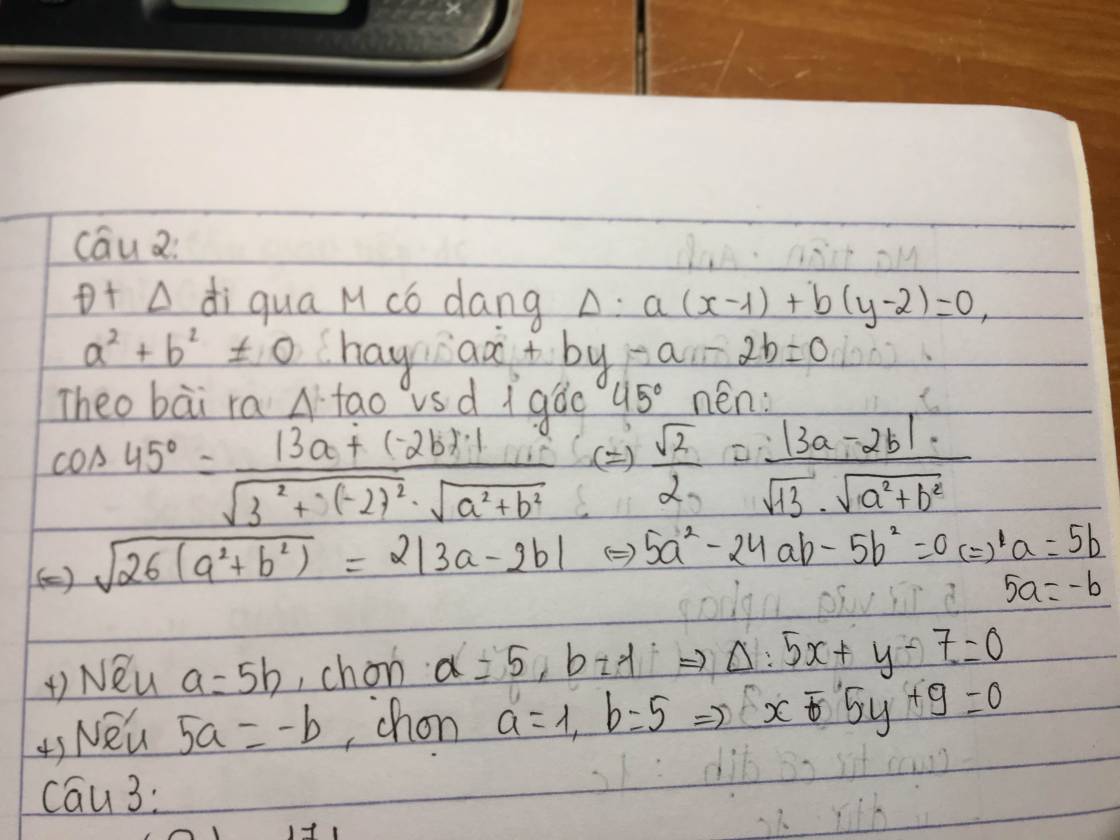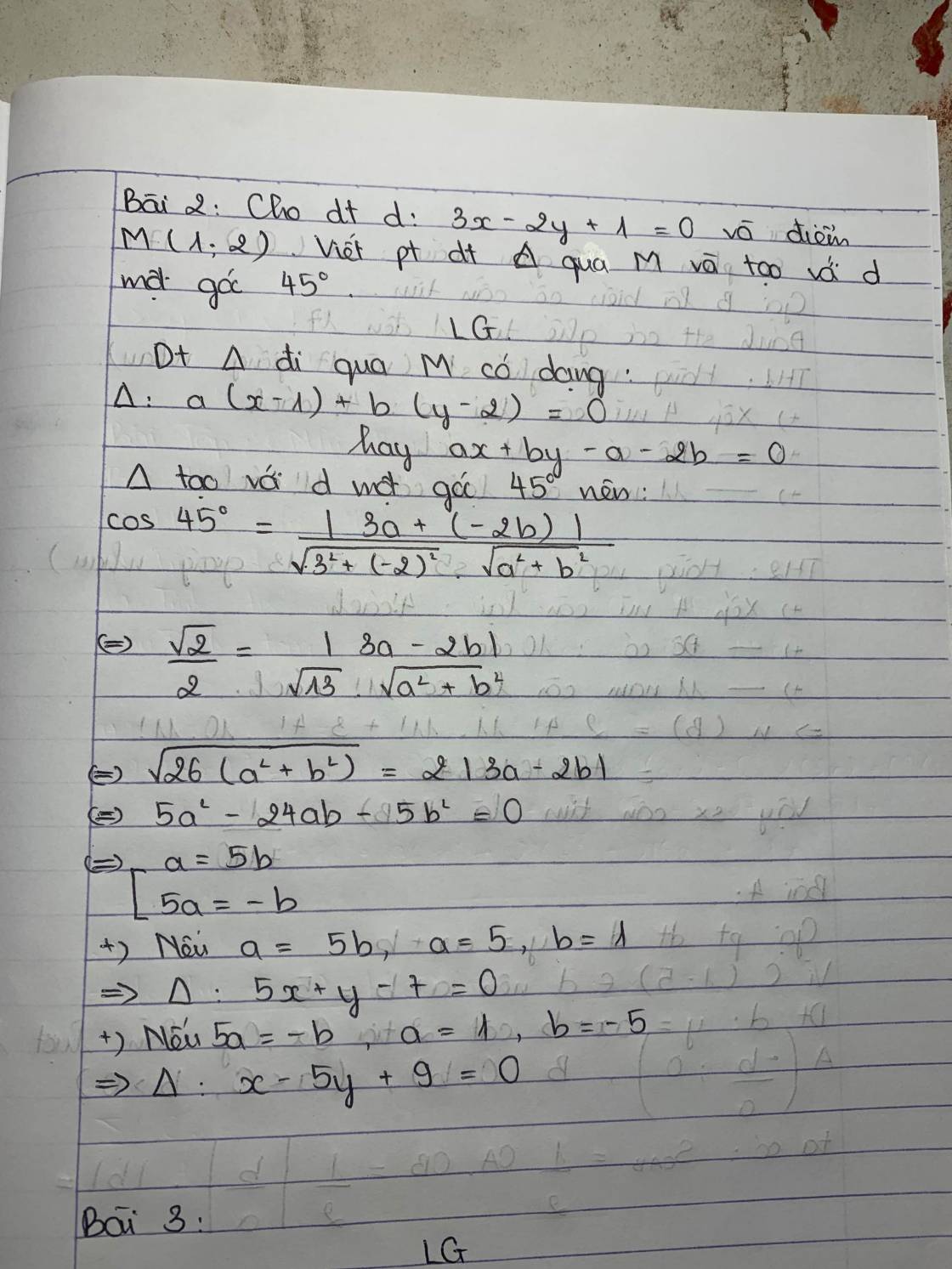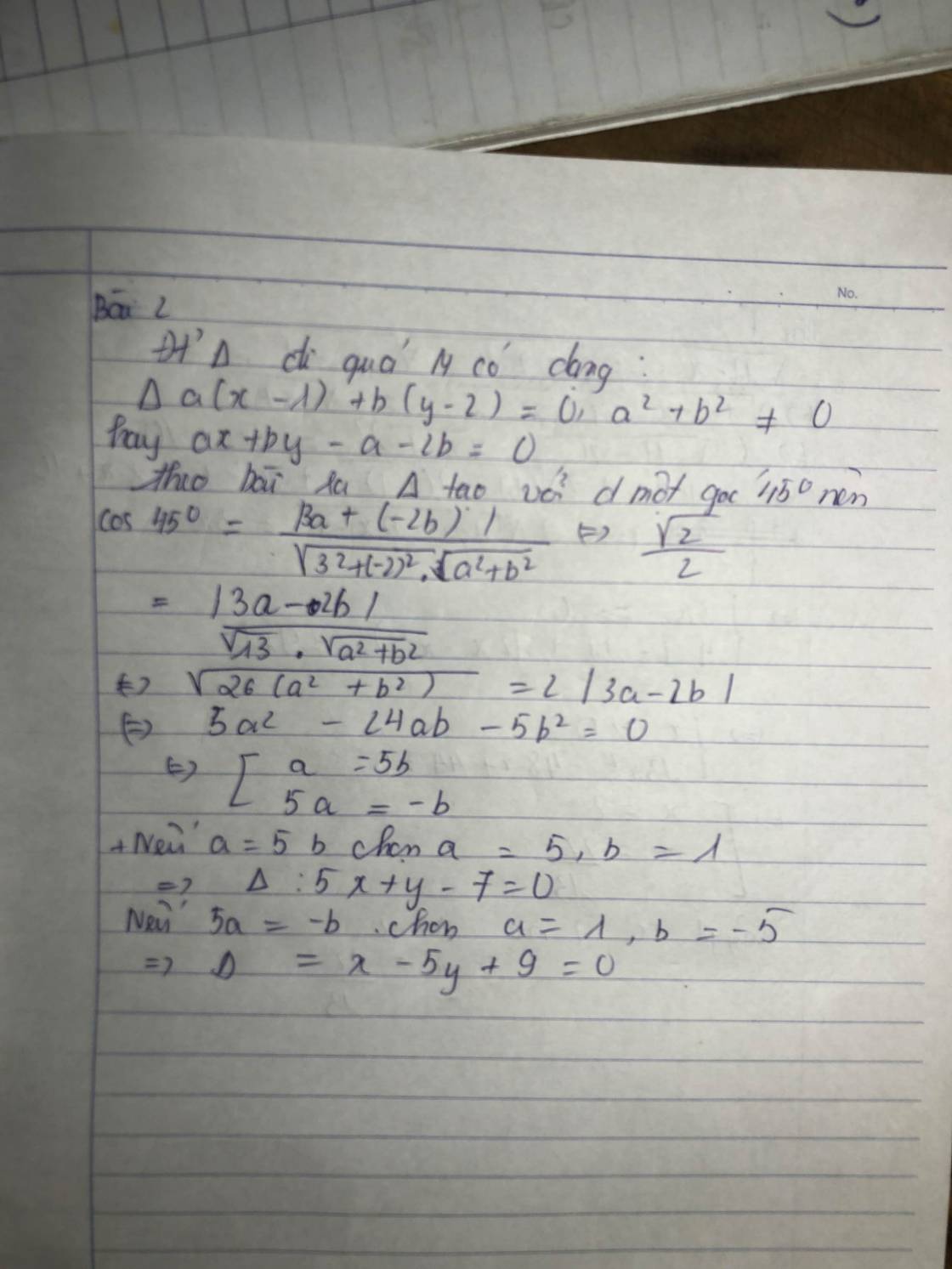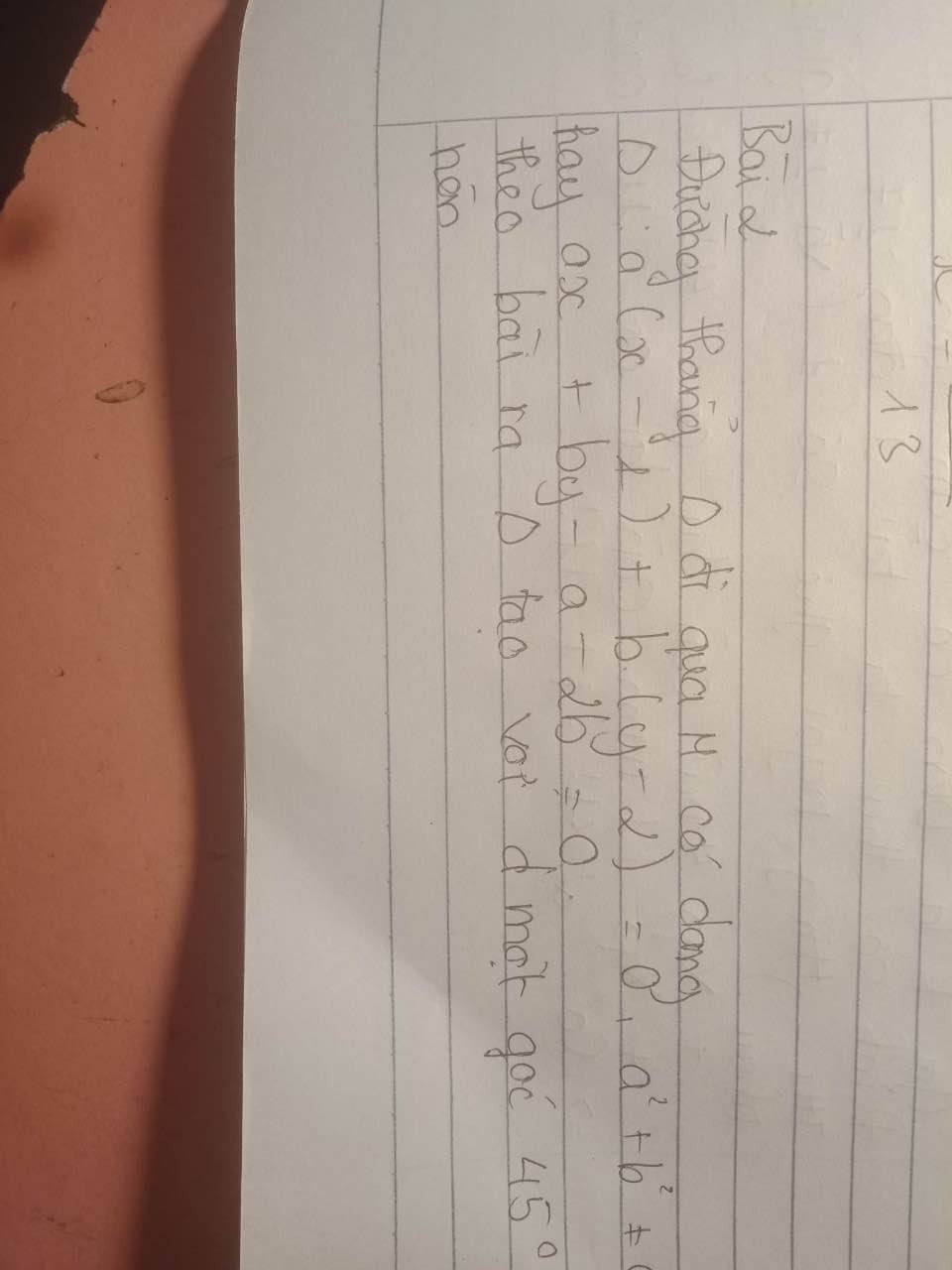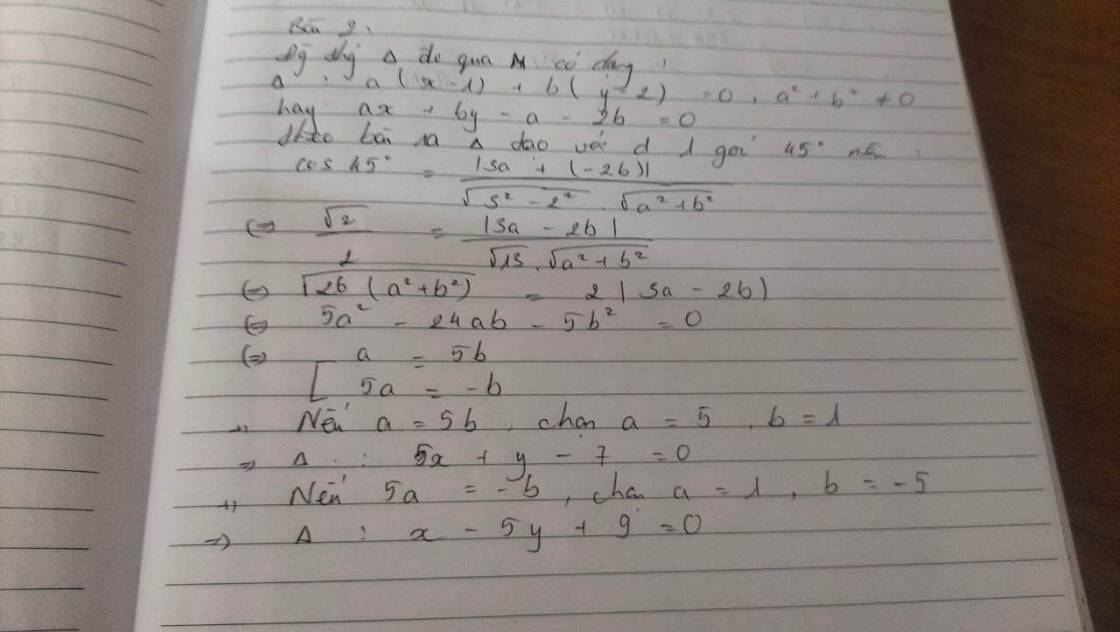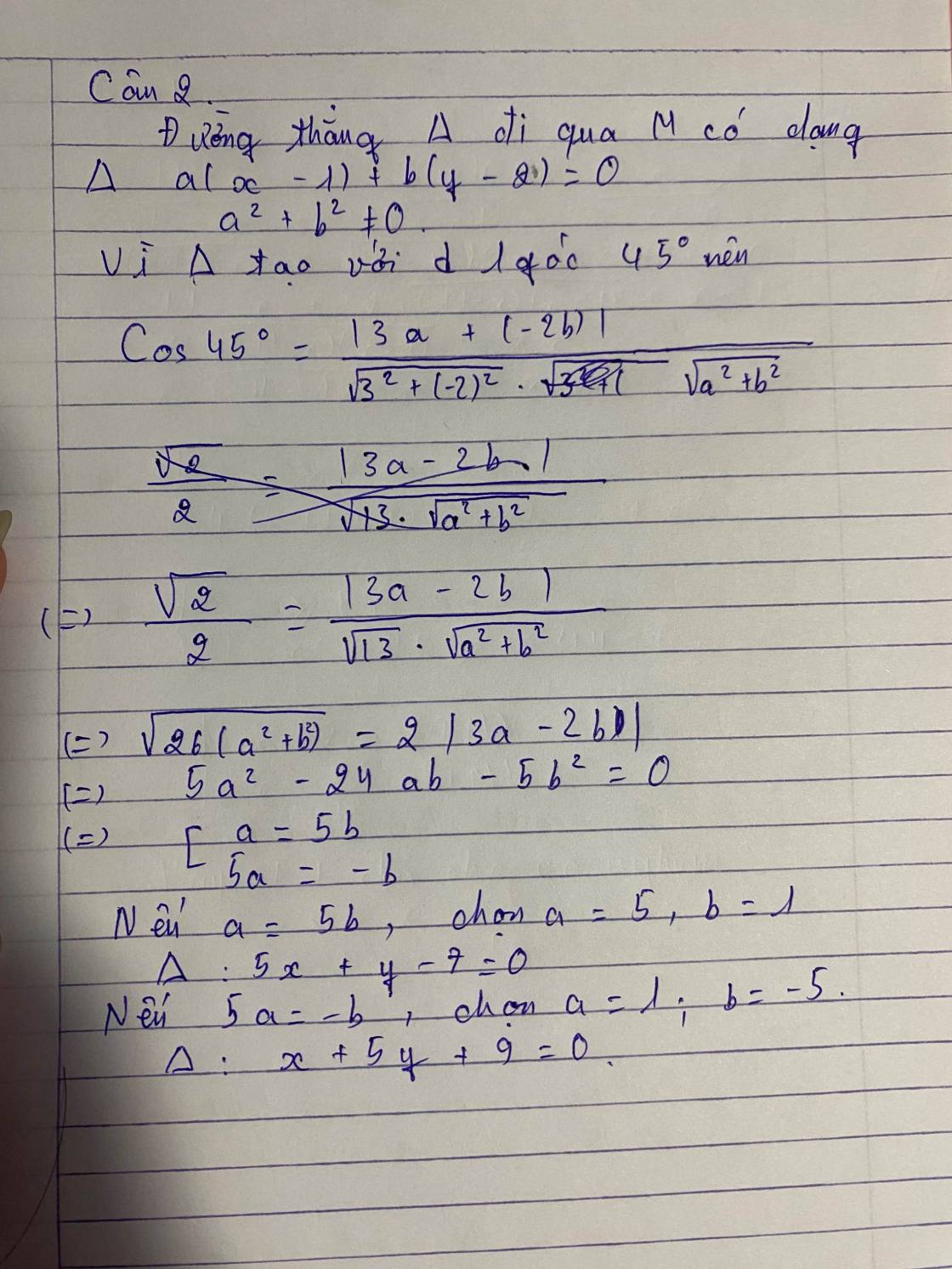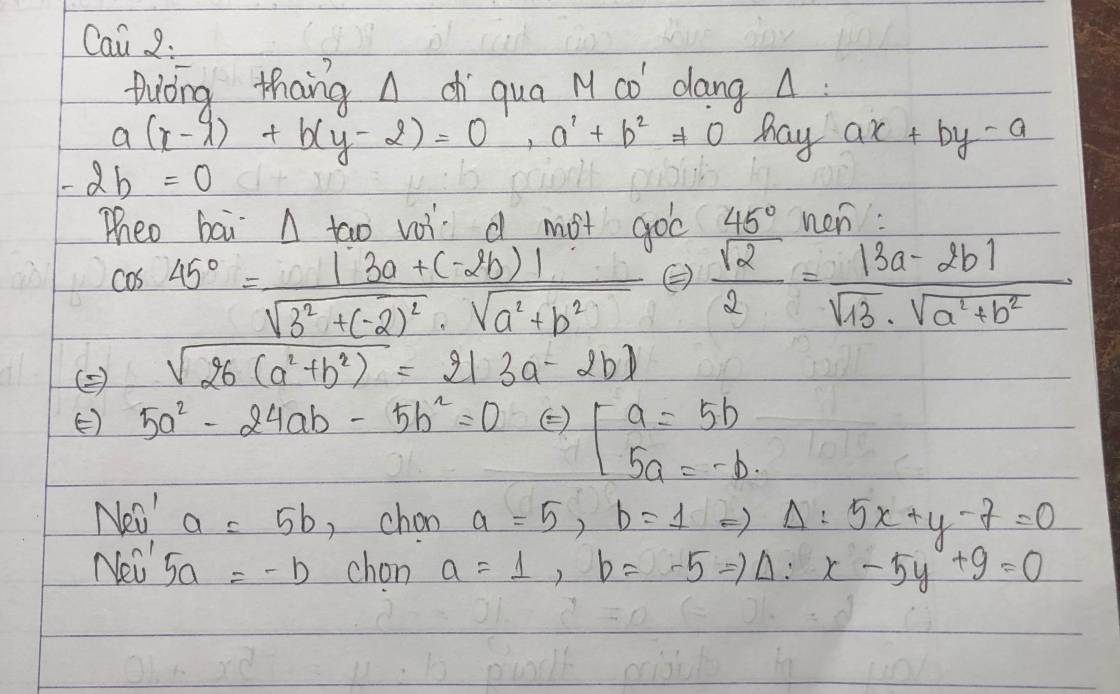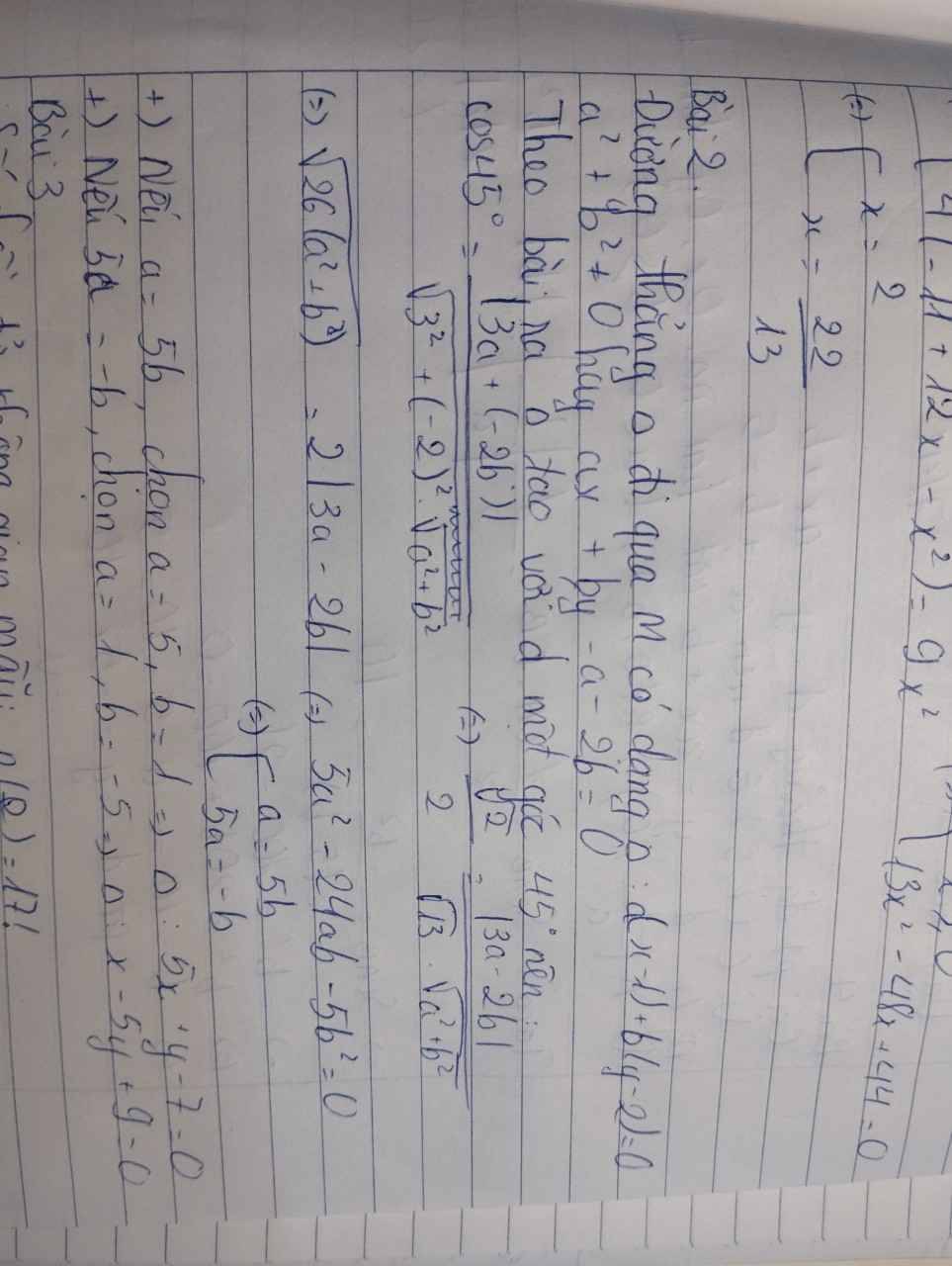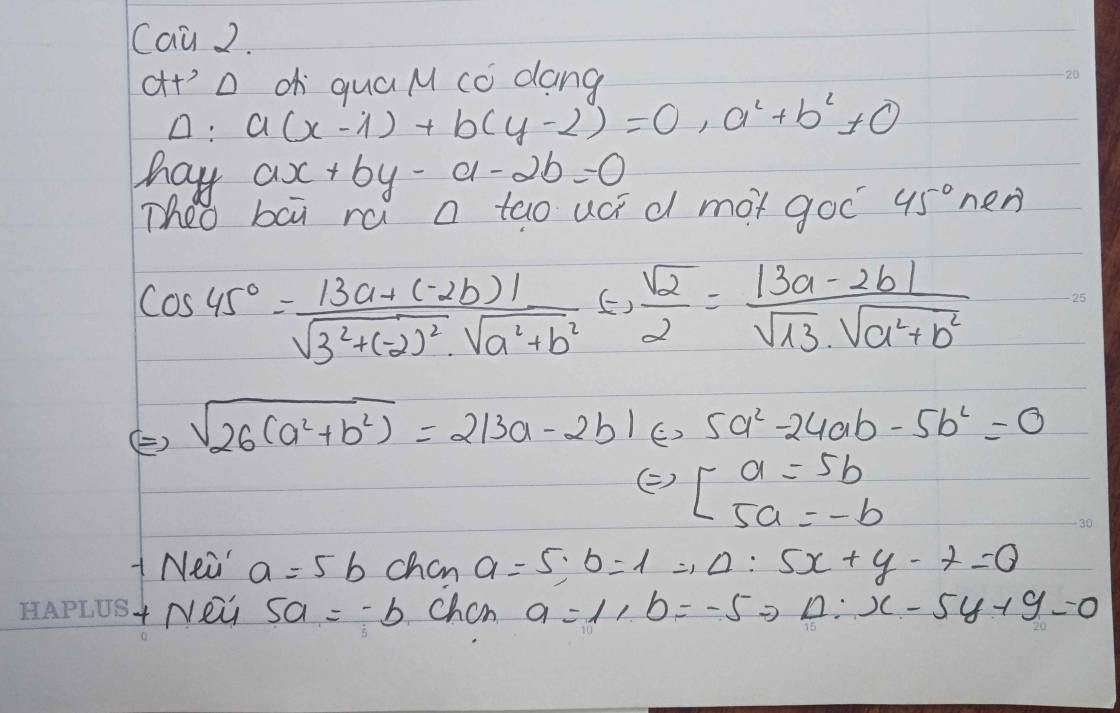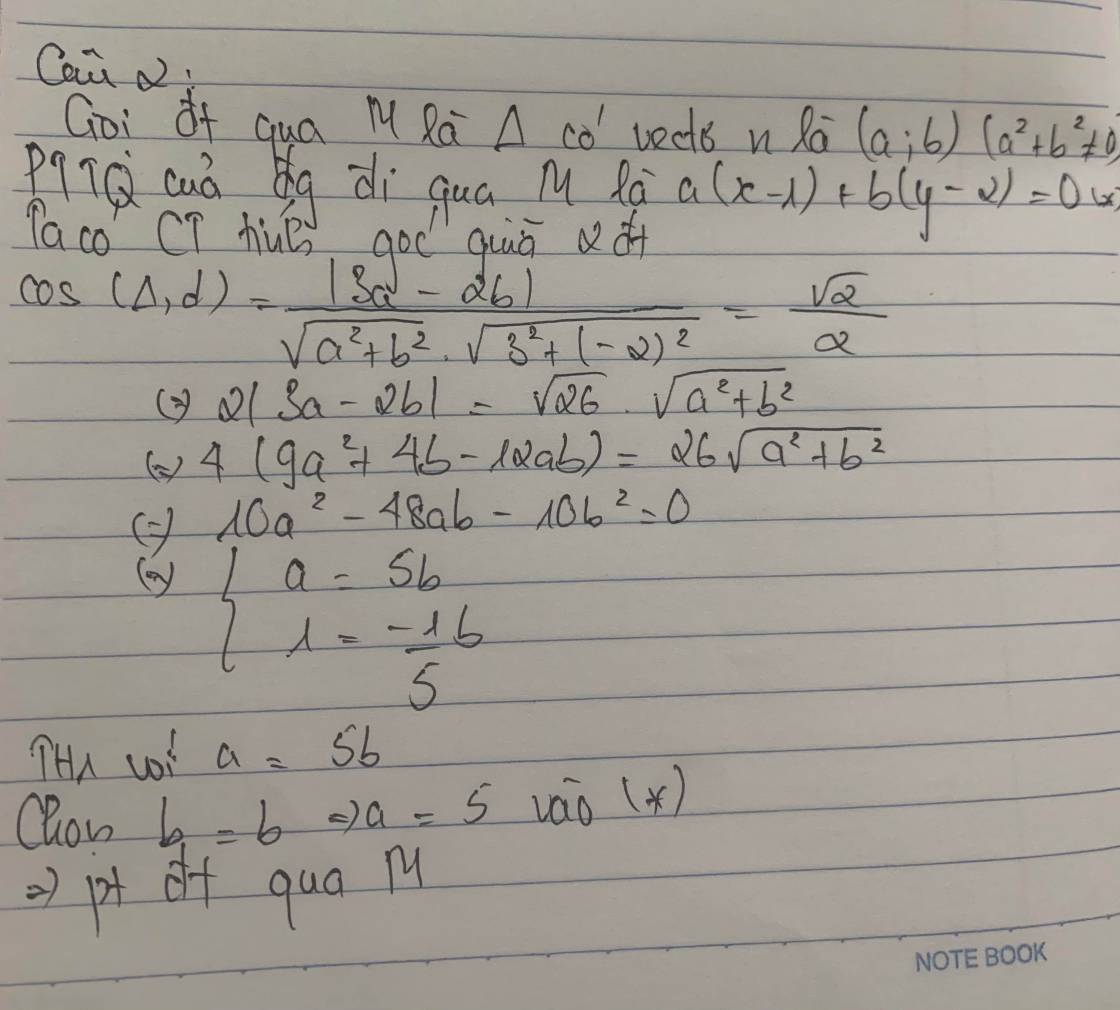Question

Câu 2. Cho đường thẳng $d:3x-2y+1=0$ và điểm $M\left( 1;2 \right)$. Viết phương trình đường thẳng $\Delta $ qua $M$ và tạo với $d$ một góc $45^{\circ}$.

Answer 1

Answer 2

gọi đường thẳng qua M là Δ có vecto n là (a;b) đk \(a^2+b^2\ne0\)

PTTQ của đg đi qua M là a(x-1)+b(y-2)=0 *

ta có CT tính góc giữa hai 2 đt 

cos (\(\Delta;d\))=\(\dfrac{\left|3a-2b\right|}{\sqrt{a^2+b^2}.\sqrt{3^2+\left(-2\right)^2}}=\dfrac{\sqrt{2}}{2}\)
\(2\left|3a-2b\right|=\sqrt{26}\sqrt{a^2+b^2}\)
\(4\left(9a^2+4b-12ab\right)=26\sqrt{a^2+b^2}\)
\(10a^2-48ab-10b^2=0\)

\(\left\{{}\begin{matrix}a=5b\\1=-\dfrac{1}{5}b\end{matrix}\right.\)

\left[{}\begin{matrix}a=5b\\a=-\dfrac{1}{5}b\end{matrix}\right.

th1 vs a=5b

chọn b=1 =>a =5 thế vào * => pt đt qua M 

th2 vs a=-\(\dfrac{1}{5}\)b

chọn b=-5 => a = 1 thế vào * => pt đt qua M

Answer 3

Answer 4

    

Answer 5

    

Answer 6

  

Answer 7

  

Answer 8

  

Answer 9

  

Answer 10

  
Δ:a(x−1)+b(y−2)=0,a2+b2≠0Δ:a(x−1)+b(y−2)=0,a2+b
ax+by−a−2b=

45∘45:

cos⁡45∘ =∣3a+(−2b)∣32+(−2)2.a2+b2⇔22=∣3a−2b∣13.a2+b2cos45∘ =32+(−2)2​.a2+b2​

Answer 11

Căn2 trên2

Answer 12

  

Answer 13

  

Answer 14

  

Answer 15

  

Answer 16

Answer 17

    

Answer 18

  

Answer 19

Đenta:x-5y+9=0

Answer 20

  

Answer 21

  

Answer 22

  

Answer 23

Theo đầu bài Δ tạo với d 1 góc 45^o :\(\cos45^o\)\(=\dfrac{\left|3a+\left(-2b\right)\right|}{\sqrt{3^2}+\left(-2\right)^2.\sqrt{a^2+b}^2}\Leftrightarrow\dfrac{\sqrt{2}}{2}=\dfrac{\left|3a-2b\right|}{\sqrt{13}.\sqrt{a^2+b^2}}\)

\(\sqrt{26\left(a^2+b^2\right)}=2\left|3a-2b\right|\Leftrightarrow5a^2-24b-5b^2=0\Leftrightarrow\left[{}\begin{matrix}a=5b\\5a=-b\end{matrix}\right.\)

+ nếu a=5 chọn a=5,b=1⇒Δ:5x+y-7=0

+ nếu 5a=-b chọn a =1,b=-5⇒Δ:x-5y+9=0

Answer 24

  

Answer 25

  

Answer 26

Answer 27

  

Answer 28

Answer 29

  

Answer 30