
Giúp em câu này với ạ. em cm ơn nhiều
Dạ giải giúp em câu này với ạ
Em cảm ơn nhiều ạ !
1: (x-1)^2+(y+2)^2=25
=>R=5; I(1;-2)
2: Δ'//Δ nên Δ': 3x-4y+c=0
d(I;Δ')=5
=>\(\dfrac{ \left|3\cdot1+\left(-2\right)\cdot\left(-4\right)+c\right|}{\sqrt{3^2+\left(-4\right)^2}}=5\)
=>|c+11|=25
=>c=14 hoặc c=-36
=>3x-4y+14=0 hoặc 3x-4y-36=0
3x-4y+14=0
=>VTPT là (3;-4) và (Δ') đi qua A(2;5)
=>VTCP là (4;3)
=>PTTS là x=2+4t và y=5+3t
3x-4y-36=0
=>VTPT là (3;-4) và (Δ') đi qua B(0;-9)
=>VTCP là (4;3)
PTTS là x=0+4t và y=-9+3t
mọi người giúp em câu này với ạ, em cám ơn nhiều ạ!

\(f\left(1-3x\right)=2\left(1-3x\right)-\left(1-3x\right)^2=1-9x^2\)
Giúp em câu này với ạ
Em cảm ơn nhiều
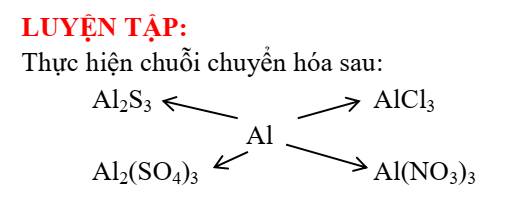
giúp em câu này với ạ em cảm ơn nhiều
\(2Al+3S\rightarrow Al_2S_3\)(điều kiện: >150 độ C)
\(2Al+3Cl_2\rightarrow2AlCl_3\)
\(4Al+3H_2SO_4\rightarrow2Al_2\left(SO_4\right)_3+3H_2\uparrow\)
\(Al+4HNO_3\rightarrow Al\left(NO_3\right)_3+NO+2H_2O\)
Giúp em câu này với ạ em cảm ơn nhiều lắm

giúp em câu này với ạ em cảm ơn nhiều lắm
Đây là bài tập hay đang kiểm tra đây em? :)
ĐKXĐ: \(x\ge0\)
Với \(x=0\) ko phải nghiệm
Với \(x>0\) chia 2 vế cho \(x\) ta được:
\(\dfrac{2x^2+1}{x}-2m=3\sqrt{\dfrac{2x^2+1}{x}}-4\)
Đặt \(\sqrt{\dfrac{2x^2+1}{x}}=t\ge\sqrt{2\sqrt{2}}=\sqrt[4]{8}\)
\(\Rightarrow2x^2-tx+1=0\) (1)
\(\Delta=t^2-8\Rightarrow\) ứng với mỗi giá trị t thì:
- Nếu \(t>2\sqrt{2}\Rightarrow\left(1\right)\) có 2 nghiệm pb
- Nếu \(t=2\sqrt{2}\Rightarrow\left(1\right)\) có 1 nghiệm kép
- Nếu \(t< 2\sqrt{2}\) thì (1) vô nghiệm
Pt đã cho trở thành \(t^2-3t+4=2m\) (2)
Xét hàm \(f\left(t\right)=t^2-3t+4\) với \(t\ge\sqrt[4]{8}\)
\(a=1>0;-\dfrac{b}{2a}=\dfrac{3}{2}< \sqrt[4]{8}\Rightarrow f\left(t\right)\) đồng biến khi \(t\ge\sqrt[4]{8}\)
\(\Rightarrow y=2m\) cắt \(y=f\left(t\right)\) tại tối đa 1 điểm hay (2) có tối đa 1 nghiệm t
\(\Rightarrow\) Pt đã cho có 2 nghiệm pb khi và chỉ khi (2) có nghiệm thỏa mãn \(t>2\sqrt{2}\)
\(\Rightarrow2m>f\left(2\sqrt{2}\right)=12-6\sqrt{2}\Rightarrow m>6-3\sqrt{2}\)
Có 19 giá trị nguyên của m
Ai giúp em câu này với em cảm ơn nhiều ạ!
a, thay x=25 vào A ta có:
\(A=\dfrac{\sqrt{x}}{\sqrt{x}-1}=\dfrac{\sqrt{25}}{\sqrt{25}-1}=\dfrac{5}{5-1}=\dfrac{5}{4}\)
b, \(P=\dfrac{\sqrt{x}}{\sqrt{x}-1}\left(\dfrac{3x+3}{x\sqrt{x}-1}-\dfrac{2}{\sqrt{x}-1}\right)\)
\(\Rightarrow P=\dfrac{\sqrt{x}}{\sqrt{x}-1}\left(\dfrac{3x+3}{\sqrt{x^3}-1}-\dfrac{2\left(x+\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\right)\)
\(\Rightarrow P=\dfrac{\sqrt{x}}{\sqrt{x}-1}\left(\dfrac{3x+3}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}-\dfrac{2x+2\sqrt{x}+2}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\right)\)
\(\Rightarrow P=\dfrac{\sqrt{x}}{\sqrt{x}-1}.\dfrac{3x+3-2x-2\sqrt{x}-2}{\left(\sqrt{x}-1\right)\left(x+\sqrt{x}+1\right)}\)
\(\Rightarrow P=\dfrac{\sqrt{x}\left(x-2\sqrt{x}+1\right)}{\left(\sqrt{x}-1\right)^2\left(x+\sqrt{x}+1\right)}\)
\(\Rightarrow P=\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)^2}{\left(\sqrt{x}-1\right)^2\left(x+\sqrt{x}+1\right)}\)
\(\Rightarrow P=\dfrac{\sqrt{x}}{x+\sqrt{x}+1}\)
Dạ Thầy cô giải giúp em câu này với ạ
Em Cảm ơn nhiều ạ

1: vecto AC=(-2;2)
=>VTCP là (-2;2); vtpt là (2;2)
2: vecto AB=(-10;-2)=(5;1)
=>VTPT của Δ là (5;1)
vtcp của Δ là (-1;5)
\(\overrightarrow{AC}=\left(-2;2\right)=2\left(-1;1\right)\) nên đường thẳng AC nhận \(\left(-1;1\right)\) là 1 vtcp và \(\left(1;1\right)\) là 1 vtpt
b.
\(\overrightarrow{BA}=\left(10;2\right)=2\left(5;1\right)\) ; mà \(\Delta\perp AB\) nên \(\Delta\) nhận (5;1) là 1 vtpt và \(\left(1;-5\right)\) là 1 vtcp
Ai giúp em câu này với ạ :(( em cảm ơn nhiều nhaaaaaa
\(=2\sqrt{3}-10\sqrt{3}-\sqrt{3}+\dfrac{5\sqrt{3}}{2}=\dfrac{5\sqrt{3}}{2}-9\sqrt{3}=\dfrac{5\sqrt{3}-18\sqrt{3}}{2}=\dfrac{-13\sqrt{3}}{2}\)
\(=\dfrac{1}{2}.4\sqrt{3}-2.5\sqrt{3}-\sqrt{3}+5.\dfrac{\sqrt{3}}{2}\)
\(=2\sqrt{3}-10\sqrt{3}-\sqrt{3}+\dfrac{5\sqrt{3}}{2}\)
\(=-9\sqrt{3}+\dfrac{5\sqrt{3}}{2}=\dfrac{-18\sqrt{3}+5\sqrt{3}}{2}=-\dfrac{13\sqrt{3}}{2}\)