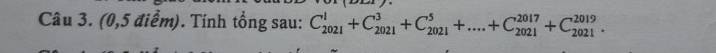Đây là bài tập hay đang kiểm tra đây em? :)
ĐKXĐ: \(x\ge0\)
Với \(x=0\) ko phải nghiệm
Với \(x>0\) chia 2 vế cho \(x\) ta được:
\(\dfrac{2x^2+1}{x}-2m=3\sqrt{\dfrac{2x^2+1}{x}}-4\)
Đặt \(\sqrt{\dfrac{2x^2+1}{x}}=t\ge\sqrt{2\sqrt{2}}=\sqrt[4]{8}\)
\(\Rightarrow2x^2-tx+1=0\) (1)
\(\Delta=t^2-8\Rightarrow\) ứng với mỗi giá trị t thì:
- Nếu \(t>2\sqrt{2}\Rightarrow\left(1\right)\) có 2 nghiệm pb
- Nếu \(t=2\sqrt{2}\Rightarrow\left(1\right)\) có 1 nghiệm kép
- Nếu \(t< 2\sqrt{2}\) thì (1) vô nghiệm
Pt đã cho trở thành \(t^2-3t+4=2m\) (2)
Xét hàm \(f\left(t\right)=t^2-3t+4\) với \(t\ge\sqrt[4]{8}\)
\(a=1>0;-\dfrac{b}{2a}=\dfrac{3}{2}< \sqrt[4]{8}\Rightarrow f\left(t\right)\) đồng biến khi \(t\ge\sqrt[4]{8}\)
\(\Rightarrow y=2m\) cắt \(y=f\left(t\right)\) tại tối đa 1 điểm hay (2) có tối đa 1 nghiệm t
\(\Rightarrow\) Pt đã cho có 2 nghiệm pb khi và chỉ khi (2) có nghiệm thỏa mãn \(t>2\sqrt{2}\)
\(\Rightarrow2m>f\left(2\sqrt{2}\right)=12-6\sqrt{2}\Rightarrow m>6-3\sqrt{2}\)
Có 19 giá trị nguyên của m