\(2x^2-2mx+3m-1\ge0\), với mọi x thuộc R

Những câu hỏi liên quan
Tìm m thuộc R để :
x2 -2mx +3m-2>0 với mọi x thuộc (\(-\infty;4\))
Để \(f\left(x\right)=x^2-2mx+3m-2>0\) \(\forall x< 4\) thì:
\(\left[{}\begin{matrix}\Delta'< 0\\\left\{{}\begin{matrix}\Delta'=0\\\frac{-b}{2a}\ge4\end{matrix}\right.\\\left\{{}\begin{matrix}\Delta'>0\\4< x_1< x_2\end{matrix}\right.\end{matrix}\right.\)
TH1: \(\Delta'< 0\Rightarrow m^2-3m+2< 0\Rightarrow1< m< 2\)
TH2: \(\left\{{}\begin{matrix}\Delta'=0\\\frac{-b}{2a}\ge4\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m^2-3m+2=0\\m\ge4\end{matrix}\right.\) \(\Rightarrow\) ko tồn tại m thỏa mãn
TH3: \(\left\{{}\begin{matrix}\Delta'>0\\4< x_1< x_2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}\Delta'>0\\a.f\left(4\right)>0\\\frac{S}{2}>4\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m^2-3m+2>0\\16-8m+3m-2>0\\m>4\end{matrix}\right.\)
\(\Rightarrow\) ko có m thỏa mãn
Vậy với \(1< m< 2\) thì \(f\left(x\right)>0\) \(\forall x< 4\)
Đúng 0
Bình luận (0)
Tìm m thỏa mãn
a) \(\dfrac{-x^2+2x-5}{x^2-mx+1}\le0\) nghiệm đúng với mọi x thuộc R
b) \(x^2-2\left(m-1\right)x+4m+8\ge0\) nghiệm đúng với mọi x thuộc R
1.Tìm m để bpt \(2\left|x-m\right|+x^2+2>2mx\) thỏa mãn với mọi x
2. Tìm m để bpt : \(x^2+2\left|x+m\right|+2mx+3m^2-3m+1< 0\) có nghiệm
1.
\(2\left|x-m\right|+x^2+2>2mx\)
\(\Leftrightarrow\left(x-m\right)^2+2\left|x-m\right|-m^2+2>0\)
\(\Leftrightarrow t^2+2t-m^2+2>0\left(t=\left|x-m\right|\ge0\right)\)
\(\Leftrightarrow m^2< f\left(t\right)=t^2+2t+2\)
Yêu cầu bài toán thỏa mãn khi \(m^2< minf\left(t\right)=2\)
\(\Leftrightarrow-\sqrt{2}< m< 2\)
Vậy \(-\sqrt{2}< m< 2\)
Đúng 0
Bình luận (0)
2.
\(x^2+2\left|x+m\right|+2mx+3m^2-3m+1< 0\)
\(\Leftrightarrow\left(x+m\right)^2+2\left|x+m\right|+2m^2-3m+1< 0\)
\(\Leftrightarrow\left(\left|x+m\right|+1\right)^2< -2m^2+3m\)
Ta có \(VT=\left(\left|x+m\right|+1\right)^2=\left(-\left|x+m\right|-1\right)^2\le\left(-1\right)^2=1\)
Yêu cầu bài toán thỏa mãn khi \(VP=-2m^2+3m>1\)
\(\Leftrightarrow2m^2-3m+1< 0\)
\(\Leftrightarrow\dfrac{1}{2}< m< 1\)
Đúng 0
Bình luận (0)
Tìm đk của m để bpt sau nghiệm đúng trên khoảng đã chỉ ra :
1. \(\left(m+1\right)x^2-2mx+4m\)> 0 với mọi x<0
2.\(_{x^2-2mx+3m-2>0}\)với x thuộc khoảng từ 1 đến 2
Cho hàm số \(y=\dfrac{2sinx+1}{\sqrt{sin^2x+\left(2m-3\right)cosx+3m-2}}\). Có bao nhiêu giá trị của m thuộc khoảng (-2023;2023) để hàm số xác định với mọi x thuộc R
Hàm số xác định trên R khi và chỉ khi:
\(sin^2x+\left(2m-3\right)cosx+3m-2>0;\forall x\in R\)
\(\Leftrightarrow-cos^2x+\left(2m-3\right)cosx+3m-1>0\)
\(\Leftrightarrow t^2-\left(2m-3\right)t-3m+1< 0;\forall t\in\left[-1;1\right]\)
\(\Leftrightarrow t^2+3t+1< m\left(2t+3\right)\)
\(\Leftrightarrow\dfrac{t^2+3t+1}{2t+3}< m\) (do \(2t+3>0;\forall t\in\left[-1;1\right]\))
\(\Leftrightarrow m>\max\limits_{\left[-1;1\right]}\dfrac{t^2+3t+1}{2t+3}\)
Ta có: \(\dfrac{t^2+3t+1}{2t+3}=\dfrac{t^2+t-2+2t+3}{2t+3}=\dfrac{\left(t-1\right)\left(t+2\right)}{2t+3}+1\)
Do \(-1\le t\le1\Rightarrow\dfrac{\left(t-1\right)\left(t+2\right)}{2t+3}\le0\)
\(\Rightarrow\max\limits_{\left[-1;1\right]}\dfrac{t^2+3t+1}{2t+3}=1\)
\(\Rightarrow m>1\)
Đúng 2
Bình luận (1)
Cho hàm số y=f(x) có đạo hàm \(f'\left(x\right)=x\left(x+1\right)^2\left(x^2+2mx+1\right)\) với mọi x thuộc R. Có bao nhiêu số nguyên âm m để hàm số \(g\left(x\right)=f\left(2x+1\right)\) đồng biến trên khoảng (3;5)
Tìm đkien của tham số m để
a) \(-x^2+mx+m+1\le0\) với mọi x ∈ R
b) Hàm số \(y=\sqrt{mx^2-2mx+2}\) xđinh với mọi x∈R
c) \(x^2+4x+\left(m-2\right)^2\le0\) vô nghiệm
d) \(\frac{x^2+x+1}{\left(3m-1\right)x^2-\left(3m+1\right)4x+m+4}< 0\) nghiệm đúng với mọi x
a, \(f\left(x\right)=-x^2+mx+m+1\)
Để f(x) \(\le0\) \(\forall x\in R\) mà \(a=-1< 0\)
\(\Leftrightarrow\Delta\le0\) \(\Leftrightarrow\Delta=m^2+4\left(m+1\right)\le0\Leftrightarrow m^2+4m+4\le0\)
\(\Leftrightarrow\left(m+2\right)^2\le0\Leftrightarrow\left(m+2\right)^2=0\Leftrightarrow m=-2\)
b, Để hàm số y xác định \(\forall x\in R\)
\(\Leftrightarrow mx^2-2mx+2\ge0\) có nghiệm \(\forall x\in R\)
\(\Leftrightarrow\left\{{}\begin{matrix}\Delta=4m^2-2.4.m\le0\\a=m>0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}0\le m\le2\\m>0\end{matrix}\right.\) \(\Leftrightarrow0< m\le2\)
a/ Do \(a=-1< 0\)
\(\Rightarrow\) Để \(f\left(x\right)\le0\) \(\forall x\in R\Leftrightarrow\Delta'\le0\)
\(\Leftrightarrow m^2+4\left(m+1\right)\le0\Leftrightarrow\left(m+2\right)^2\le0\)
\(\Rightarrow m=-2\)
b/ Để hàm số xác định với mọi x
\(\Leftrightarrow f\left(x\right)=mx^2-2mx+2\ge0\) \(\forall x\)
- Với \(m=0\Rightarrow f\left(x\right)=2\) thỏa mãn
- Với \(m\ne0\Leftrightarrow\left\{{}\begin{matrix}m>0\\\Delta'=m^2-2m\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m>0\\0< m< 2\end{matrix}\right.\)
Vậy \(0\le m< 2\)
c/
Do \(a=1>0\)
Nên để BPT đã cho vô nghiệm
\(\Leftrightarrow f\left(x\right)=x^2+4x+\left(m-2\right)^2>0\) \(\forall x\)
\(\Leftrightarrow\Delta'=4-\left(m-2\right)^2< 0\)
\(\Leftrightarrow\left(m-2\right)^2>4\Leftrightarrow\left[{}\begin{matrix}m-2>2\\m-2< -2\end{matrix}\right.\) \(\Leftrightarrow\left[{}\begin{matrix}m>4\\m< 0\end{matrix}\right.\)
d/
Do \(x^2+x+1=\left(x+\frac{1}{2}\right)^2+\frac{3}{4}>0\) \(\forall x\)
\(\Rightarrow\) Để BPT nghiệm đúng với mọi x thì:
\(f\left(x\right)=\left(3m-1\right)x^2-\left(3m+1\right)x+m+4< 0\)
Ủa đề là \(\left(3m-1\right)x^2-\left(3m+1\right)x+m+4\) hay \(\left(3m-1\right)x^2-\left(3m+1\right)4x+m+4\) vậy bạn?
1,với giá trị nào của a thì bpt \(ax^2-x+a\ge0,\forall x\in R\)
2,cho f(x)=\(-2x^2+\left(m+2\right)x+m-4\) tìm m để f(x) âm với mọi x
3,tìm m để x2-2(2m-3)x+4m-3>0, với mọi x thuộc R
4, cho f(x)=mx2-2x-1. Xác định m để f(x)<0 với mọi x thuôc R
1, BPT đúng với mọi x thuộc R khi vầ chỉ khi:
\(\left\{{}\begin{matrix}a>0\\\Delta\le0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a>0\\1-4a^2\le0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}a>0\\a\le\frac{-1}{2};a\ge\frac{1}{2}\end{matrix}\right.\)
\(\Rightarrow a\ge\frac{1}{2}\)
2, điều kiện: \(\Delta< 0\\ \Leftrightarrow\left(m+2\right)^2+8\left(m-4\right)< 0\\ \Leftrightarrow m^2+12m-28< 0\\ \Leftrightarrow-14< m< 2\)
3, điều kiện: \(\Delta'< 0\\ \Leftrightarrow\left(2m-3\right)^2-\left(4m-3\right)< 0\\ \Leftrightarrow m^2-4m+3< 0\\ \Leftrightarrow1< m< 3\)
4, Nếu m=0 => f(x)=-2x-1<0 (loại)
Nếu m≠0 để f(x)<0 với ∀x ϵ R khi và chỉ khi:
\(\left\{{}\begin{matrix}m< 0\\\Delta'< 0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}m< 0\\1+m< 0\end{matrix}\right.\)
\(\Rightarrow m< -1\)
Đúng 0
Bình luận (0)
Tìm m để các hàm số
f
(
x
)
2
x
-
4
+
3
...
Đọc tiếp
Tìm m để các hàm số f ( x ) = 2 x - 4 + 3 K h i x ≥ 2 x + 1 x 2 - 2 m x + 3 m + 2 K h i x < 2 liên tục trên R
A. 1
B. 2
C. 5
D. 4
Chọn C.
Với x > 2 ta có hàm số liên tục
Để hàm số liên tục trên R thì hàm số phải liên tục trên khoảng (-∞; 2) và liên tục tại x = 2.
- Hàm số liên tục trên (-∞; 2) khi và chỉ khi tam thức
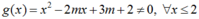
TH 1: 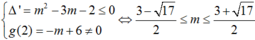
TH 2: 

Nên 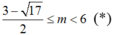 thì
thì ![]()
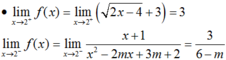
Hàm số liên tục tại  (thỏa (*))
(thỏa (*))
Đúng 0
Bình luận (0)


















