Giải hộ mình câu 28 với ạ 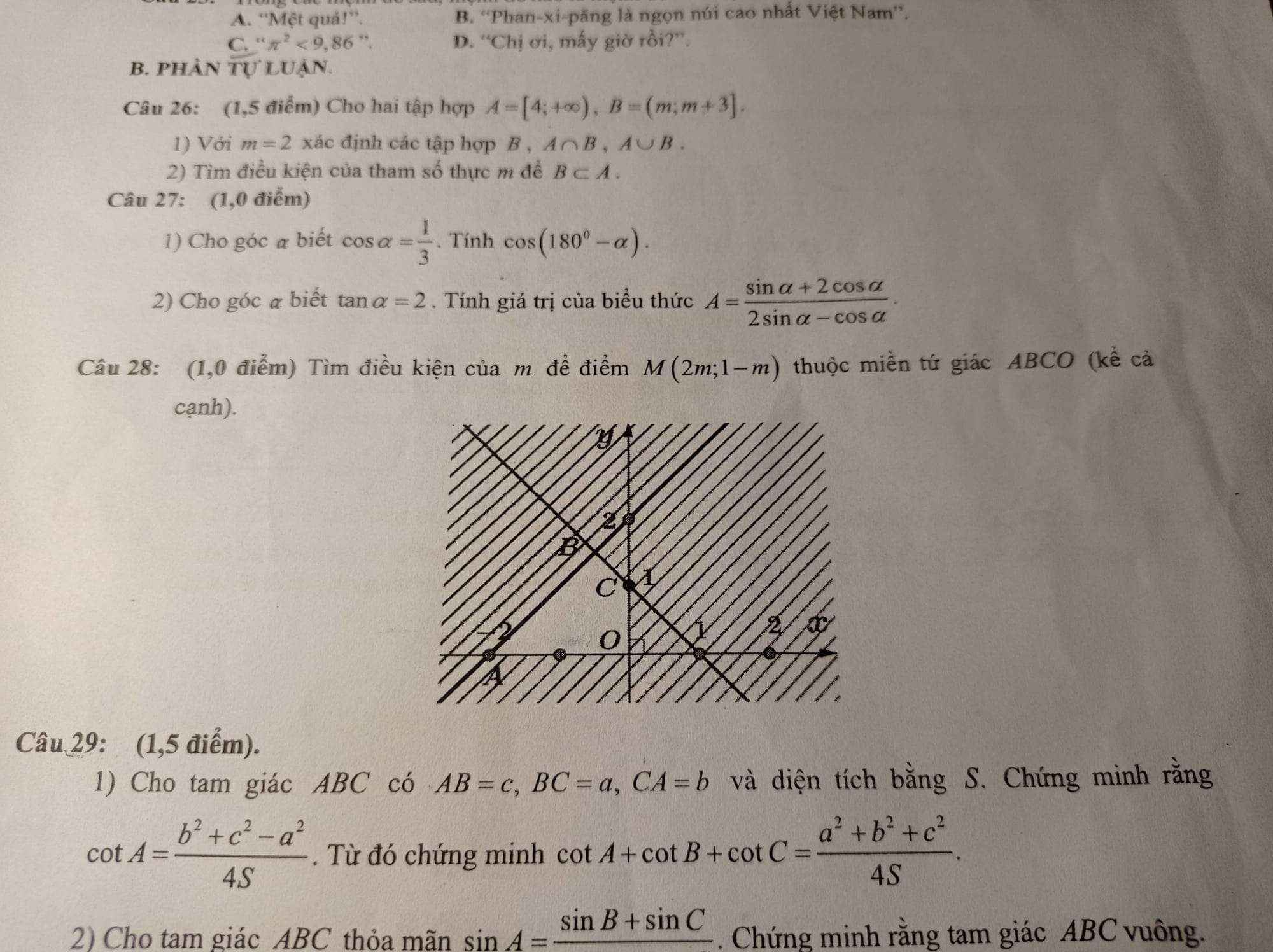

Những câu hỏi liên quan
Giải hộ mình câu c bài này với ạ, mình cảm ơn nhiều nhiều ^^
Mình đag cần gấp, làm nhanh hộ mình với ạ <3

ext-9bosssssssssssssssss

làm giúp mình câu 5 :câu 3 với!giải dõ hộ mình với ạ!
Câu 1: D
Câu 2: C
Câu 3: C
Câu 4: D
Câu 5: A
Đúng 0
Bình luận (1)
Giải hộ mình câu c bài này với ạ, mình cảm ơn nhiều nhiều ^^
Mình đag cần gấp lắm ạ, làm nhanh hộ mình với <3
Cảm ơn lần nữa

1) Vì x=25 thỏa mãn ĐKXĐ nên Thay x=25 vào biểu thức \(A=\dfrac{\sqrt{x}-2}{x+1}\), ta được:
\(A=\dfrac{\sqrt{25}-2}{25+1}=\dfrac{5-2}{25+1}=\dfrac{3}{26}\)
Vậy: Khi x=25 thì \(A=\dfrac{3}{26}\)
2) Ta có: \(B=\dfrac{\sqrt{x}-3}{\sqrt{x}+1}+\dfrac{2x+8\sqrt{x}-6}{x-\sqrt{x}-2}\)
\(=\dfrac{\left(\sqrt{x}-3\right)\left(\sqrt{x}-2\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}+\dfrac{2x+8\sqrt{x}-6}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{x-5\sqrt{x}+6+2x+8\sqrt{x}-6}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{3x+3\sqrt{x}}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{3\sqrt{x}\left(\sqrt{x}+1\right)}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+1\right)}\)
\(=\dfrac{3\sqrt{x}}{\sqrt{x}-2}\)
Đúng 0
Bình luận (0)
 giải hộ mình với ạ, câu 34 đến 40 lun ạ
giải hộ mình với ạ, câu 34 đến 40 lun ạ
câu 34:
điện trở là:
R=(U)2/\(\rho\)hoa=(6)2/3=12(\(\Omega\))
điện năng tiêu thụ là:
A=\(\rho\)hoa.t=3.14400=43200(J)
mai làm típ :)
Đúng 5
Bình luận (0)
Em ơi chỉ đc hỏi tối đa 3 câu tự luận nha, em vui lòng đăng câu hỏi mới nha
Đúng 2
Bình luận (0)
giải hộ mình câu 7,8,9 với ạ. Mình cảm ơn
Chữ mờ quá. Bạn nên gõ đề bằng công thức toán để được hỗ trợ tốt hơn.
Đúng 1
Bình luận (0)
giải hộ mình câu 85,90 với ạ mình cảm ơn
giải hộ mình câu này với mình cảm ơn ạ
( x +1 ) + ( x+4) + ( x +7) + .... ( x +28 ) =155
Ai Làm Và giải thích cách làm hộ mình với ạ
(x+1)+(x+4)+(x+7)+....+(x+28)=155
=>10x+(1+4+....+28)=155
=>10x+[10(1+28)]/2=155
=>10x+145=155
=>10x=10
=>x=1
Đúng 1
Bình luận (0)
đầu tiên là ta tìm có bao nhiêu số x , ta lấy (28-1):3+1 = 10 (số) . Vậy là có 10 số x và 10 số cộng với x . Rồi ta sẽ tìm tổng của các số cộng với x , ta có : (28+1)x10:2= 145 . Sau đó ta lấy tổng của x và các số kia trừ đi tổng các số cộng với x , đó là : 155-145=10 . Rồi ta lấy 10 đó chia cho 10 số x để tìm 1 số x , ta có : 10:10=1 . Vậy x=1. (nếu đúng thì tick cho tớ nhé ! ) cái này là tớ tự suy luận mà ra .
Đúng 0
Bình luận (0)
Giải chi tiết của em đây nhé
( \(x\) + 1) + ( \(x\) + 4) + ( \(x\) + 7) +....+ ( \(x\) + 28) = 155
Xét dãy số:
\(x+1;\) \(x+4\); \(x+7\); ........: \(x+28\)
Khoảng cách của dãy số trên là: \(x\) + 4 - ( \(x\) + 1) = 3
Số số hạng của dãy số trên là:
{( \(x\) + 28) - ( \(x\) + 1) } : 3 + 1 = 10
Áp dụng công thức tính tổng dãy số cách đều ta có:
(\(x\) + 1 + \(x\) + 28) \(\times\) 10 : 2 = 155
(\(2x+29\)) \(\times\) 5 = 155
2\(x\) + 29 = 155 : 5
2\(x\) + 29 = 31
2\(x\) = 31 - 29
2\(x\) = 2
\(x\) = 2 : 2
\(x\) = 1
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Giải hộ mình câu 17,18 với ạ
nMg = 2.4/24 = 0.1 (mol)
Mg + 2HCl => MgCl2 + H2
0.1.......0.2..........0.1........0.1
mMgCl2 = 0.1*95 = 9.5 (g)
VH2 = 0.1*22.4 = 2.24 (l)
CM HCl = 0.2/0.4 = 0.5 (M)
Đúng 1
Bình luận (0)
Câu 17 :
\(a) Mg + 2HCl \to MgCl_2 + H_2\\ b) n_{MgCl_2} = n_{H_2} = n_{Mg} = \dfrac{2,4}{24} = 0,1(mol)\\ m_{MgCl_2} = 0,1.95 = 9,5(gam)\\ V_{H_2} = 0,1.22,4 = 2,24(lít)\\ c) n_{HCl} =2 n_{Mg} = 0,2(mol)\\ C_{M_{HCl}} = \dfrac{0,2}{0,4} = 0,5M\)
Đúng 0
Bình luận (0)
giải hộ mình câu 5,6,7 với ạ
Câu 5:
\(y=1-\left(sin2x+cos2x\right)^3\)
\(=1-\left[\sqrt{2}sin\left(2x+\dfrac{\pi}{4}\right)\right]^3\)\(=1-2\sqrt{2}.sin^3\left(2x+\dfrac{\pi}{4}\right)\)
Có \(-1\le sin\left(2x+\dfrac{\pi}{4}\right)\le1\)
\(\Leftrightarrow-1\le sin^3\left(2x+\dfrac{\pi}{4}\right)\le1\) \(\Leftrightarrow1+2\sqrt{2}\ge y\ge1-2\sqrt{2}\)
\(\Rightarrow y_{min}=1-2\sqrt{2}\Leftrightarrow sin\left(2x+\dfrac{\pi}{4}\right)=1\)\(\Leftrightarrow x=\dfrac{\pi}{8}+k\pi\left(k\in Z\right)\)
\(\Rightarrow y_{max}=1+2\sqrt{2}\Leftrightarrow sin\left(2x+\dfrac{\pi}{4}\right)=-1\)\(\Leftrightarrow x=\dfrac{-3\pi}{8}+k\pi\left(k\in Z\right)\)
Ý B
Đúng 1
Bình luận (0)
Câu 6: Hàm số có TXĐ: D=R
\(y=\sqrt{4-2sin^52x}-8\)
Có \(-1\le sin2x\le1\)
\(\Leftrightarrow-1\le sin^52x\le1\)
\(\Leftrightarrow2\ge-2sin^52x\ge-2\)
\(\Leftrightarrow\)\(\sqrt{6}-8\ge y\ge\sqrt{2}-8\)
Ý A
Câu 7: TXĐ: D=R
\(y=\dfrac{3}{3-\sqrt{1-cosx}}\)
Có \(-1\le cosx\le1\) \(\Leftrightarrow2\ge1-cosx\ge0\) \(\Leftrightarrow3-\sqrt{2}\ge3-\sqrt{1-cosx}\ge3\)
\(\Leftrightarrow\dfrac{3}{3-\sqrt{2}}\le y\le1\)
Vậy \(y_{min}=\dfrac{3}{3-\sqrt{2}}\Leftrightarrow x=\pi+k2\pi\) (k nguyên)
\(y_{max}=1\Leftrightarrow x=k2\pi\) (k nguyên)
Đúng 2
Bình luận (1)





























