Ta có

( 2 x 4   –   3 x 3   +   x 2 )   :   - 1 2 x 2   +   4 ( x   –   1 ) 2   =   0 ⇔   2 x 4 : ( - 1 2 x 2 ) - 3 x 3 : ( - 1 2 x 2 ) + x 2 : ( - 1 2 x 2 ) + 4 ( x 2 - 2 x + 1 ) = 0 ⇔   - 4 x 2   +   6 x   –   2   +   4 x 2   –   8 x   +   4   =   0

ó -2x + 2 = 0

ó x  = 1

Đáp án cần chọn là: C

Câu c nha bạn

1.

a/ \(\Leftrightarrow\left(x+1\right)\left(x^2+3x+2\right)+\left(x-1\right)\left(x^2-3x+2\right)-12=0\)

\(\Leftrightarrow\left(x+1\right)\left(x^2+2\right)+3x\left(x+1\right)-3x\left(x-1\right)+\left(x-1\right)\left(x^2+2\right)-12=0\)

\(\Leftrightarrow2x\left(x^2+2\right)+6x^2-12=0\)

\(\Leftrightarrow x^3+3x^2+2x-6=0\)

\(\Leftrightarrow\left(x-1\right)\left(x^2+4x+6\right)=0\Rightarrow x=1\)

b/ Nhận thấy \(x=0\) ko phải nghiệm, chia 2 vế cho \(x^2\)

\(x^2+\frac{1}{x^2}+3\left(x+\frac{1}{x}\right)+4=0\)

Đặt \(x+\frac{1}{x}=t\Rightarrow x^2+\frac{1}{x^2}=t^2-2\)

\(t^2-2+3t+4=0\Rightarrow t^2+3t+2=0\Rightarrow\left[{}\begin{matrix}t=-1\\t=-2\end{matrix}\right.\)

\(\Rightarrow\left[{}\begin{matrix}x+\frac{1}{x}=-1\\x+\frac{1}{x}=-2\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x^2+x+1=0\left(vn\right)\\x^2+2x+1=0\end{matrix}\right.\) \(\Rightarrow x=-1\)

1c/

\(\Leftrightarrow x^5+x^4-2x^4-2x^3+5x^3+5x^2-2x^2-2x+x+1=0\)

\(\Leftrightarrow x^4\left(x+1\right)-2x^3\left(x+1\right)+5x^2\left(x+1\right)-2x\left(x+1\right)+x+1=0\)

\(\Leftrightarrow\left(x+1\right)\left(x^4-2x^3+5x^2-2x+1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=-1\\x^4-2x^3+5x^2-2x+1=0\left(1\right)\end{matrix}\right.\)

\(\left(1\right)\Leftrightarrow x^4-2x^3+x^2+x^2-2x+1+3x^2=0\)

\(\Leftrightarrow\left(x^2-x\right)^2+\left(x-1\right)^2+3x^2=0\)

\(\Leftrightarrow\left\{{}\begin{matrix}x^2-x=0\\x-1=0\\x=0\end{matrix}\right.\) \(\Rightarrow\) không tồn tại x thỏa mãn

Vậy pt có nghiệm duy nhất \(x=-1\)

2.

a. \(x^4-x^3+x^2+x^2-x+1=0\)

\(\Leftrightarrow x^2\left(x^2-x+1\right)+x^2-x+1=0\)

\(\Leftrightarrow\left(x^2+1\right)\left(x^2-x+1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x^2+1=0\left(vn\right)\\x^2-x+1=0\Leftrightarrow\left(x-\frac{1}{2}\right)^2+\frac{3}{4}=0\left(vn\right)\end{matrix}\right.\)

Vậy pt vô nghiệm

b.

\(x^4+x^3+x^2+x+1=0\)

\(\Leftrightarrow x\left(x^3+1\right)+x^3+1+x^2=0\)

\(\Leftrightarrow\left(x+1\right)\left(x^3+1\right)+x^2=0\)

\(\Leftrightarrow\left(x+1\right)^2\left(x^2-x+1\right)+x^2=0\)

Mà \(\left\{{}\begin{matrix}\left(x+1\right)^2\left(x^2-x+1\right)\ge0\\x^2\ge0\end{matrix}\right.\)

Nên dấu "=" xảy ra khi và chỉ khi: \(\left\{{}\begin{matrix}x+1=0\\x=0\end{matrix}\right.\) ko tồn tại x thỏa mãn

a) x = -1.                      b) x = 4 hoặc x = 5.

c) x = ± 2 .                  d) x = 1 hoặc x = 2.

a) Ta có x 6 + 2 x 3 + 3 x 3 − 1 . 3 x x + 1 . x 2 + x + 1 x 6 + 2 x 3 + 3 = 3 x x 2 − 1  

b) Gợi ý: a 3   +   2 a 2  - a - 2 = (a - 1)(a + 1) (a + 2)

Thực hiện phép tính từ trái qua phải thu được:  = 1 3

X1+X2=X3+X4=X5+X6=2

nên X1+X2+X3+X4+X5+X6=0

2+2+2=0

6=0(loại)

vậy không có giá trị nào thỏa mãn đề

g(x) = -5 + 3x⁹ - 2x + 3x² + x⁶ + 2x - 3x³ - 3x²

= -5 + (-2x + 2x) + (3x² - 3x²) - 3x³ + x⁶ + 3x⁹

= -5 - 3x³ + x⁶ + 3x⁹

g(x) = -5 + 3x⁹ - 2x + 3x² + x⁶ + 2x - 3x³ - 3x²

= -5 + (-2x + 2x) + (3x² - 3x²) - 3x³ + x⁶ + 3x⁹

= -5 - 3x³ + x⁶ + 3x⁹

Bài 1: 

a) Ta có: \(-ax\left(xy^3\right)^2\cdot\left(-by\right)^3\)

\(=-a\cdot x\cdot x^2\cdot y^6\cdot\left(-b\right)^3\cdot y^3\)

\(=abx^3y^9\)

b) Ta có: \(xy\cdot\left(-ax\right)^2\cdot\left(-by\right)^3\)

\(=xy\cdot a^2\cdot x^2\cdot b^3\cdot y^3\)

\(=a^2b^3x^3y^4\)

Bài 2: 

Ta có: \(P\left(x\right)=5x-4x^4+x^6+3-2x^3-7x-x^7+1-2x^6+3x^3+x^7\)

\(=\left(-x^7+x^7\right)+\left(x^6-2x^6\right)-4x^4+\left(-2x^3+3x^3\right)+\left(5x-7x\right)+\left(3+1\right)\)

\(=-x^6-4x^4+x^3-2x+4\)

1. Thu gọn đơn thức sau, cho biết phần hệ số, phần biến, bậc của đơn thức(x,y là biến)

a. -ax(xy³)²(-by)³

b. xy(-ax)²(-by)3    

Giải :

a. \(-ax\left(xy^3\right)^2\left(-by\right)^3=-a\cdot x\cdot x^2\cdot\left(y^3\right)^2\cdot\left(-b\right)^3\cdot y^3=-a\cdot\left(-b\right)^3\cdot\left(x\cdot x^2\right)\cdot\left(y^6\cdot y^3\right)=ab^3x^3y^9\)

Phần hệ số : ab³ . Phần biến x³y⁹

Bậc của đơn thức : 3+9=12

b. \(xy\left(-ax\right)^2\left(-by\right)^3=-a^2b^3x^3y^3\)

Phần hệ số : -a²b³. phần biến x³y³

Bậc : 3+3=6

Ta đặt và thực hiện phép tính P(x) + Q(x) và P(x) – Q(x) có

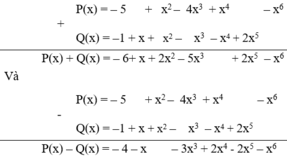
Vậy: P(x) + Q(x) = – 6 + x + 2x2 – 5x3 + 2x5 – x6

P(x) – Q(x) = – 4 – x – 3x3 + 2x4 - 2x5 – x6

Bài 1:

a) \(\Rightarrow3x^2+3x-2x^2-4x+x+1=0\)

\(\Rightarrow x^2=-1\left(VLý\right)\Rightarrow S=\varnothing\)

b) \(\Rightarrow\left(x-2020\right)\left(2x-1\right)=0\)

\(\Rightarrow\left[{}\begin{matrix}x=2020\\x=\dfrac{1}{2}\end{matrix}\right.\)

c) \(\Rightarrow\left(x-10\right)\left(x+2\right)=0\)

\(\Rightarrow\left[{}\begin{matrix}x=10\\x=-2\end{matrix}\right.\)

d) \(\Rightarrow\left(x+4\right)^2=0\Rightarrow x=-4\)

e) \(\Rightarrow\left(x+6\right)\left(x-7\right)=0\)

\(\Rightarrow\left[{}\begin{matrix}x=-6\\x=7\end{matrix}\right.\)

f) \(\Rightarrow\left(5x-4\right)\left(5x+4\right)=0\)

\(\Rightarrow\left[{}\begin{matrix}x=\dfrac{4}{5}\\x=-\dfrac{4}{5}\end{matrix}\right.\)

Bài 2:

a) \(\Rightarrow3x\left(x^2-4\right)=0\Rightarrow3x\left(x-2\right)\left(x+2\right)=0\)

\(\Rightarrow\left[{}\begin{matrix}x=0\\x=2\\x=-2\end{matrix}\right.\)

b) \(\Rightarrow x\left(x-2\right)+5\left(x-2\right)=0\Rightarrow\left(x-2\right)\left(x+5\right)=0\)

\(\Rightarrow\left[{}\begin{matrix}x=2\\x=-5\end{matrix}\right.\)

a) (2x - 5)² - (5 + 2x) = 0

<=> 4x² - 22x + 20 = 0 

\(\Leftrightarrow\left(2x-\dfrac{11}{2}\right)^2=\dfrac{41}{4}\)

\(\Leftrightarrow x=\dfrac{\pm\sqrt{41}+11}{4}\)

b) \(27x^3-54x^2+36x=0\)

\(\Leftrightarrow x\left(3x^2-6x+4\right)=0\)

\(\Leftrightarrow x=0\) (Vì \(3x^2-6x+4=3\left(x-1\right)^2+1>0\forall x\))

c) x³ + 8 - (x + 2).(x - 4) = 0

\(\Leftrightarrow\left(x+2\right).\left(x^2-2x+4\right)-\left(x+2\right)\left(x-4\right)=0\)

\(\Leftrightarrow\left(x+2\right)\left(x^2-3x+8\right)=0\)

\(\Leftrightarrow x=-2\) (Vì \(x^2-3x+8=\left(x-\dfrac{3}{2}\right)^2+\dfrac{23}{4}>0\))

d) \(x^6-1=0\)

\(\Leftrightarrow\left(x^2\right)^3-1=0\)

\(\Leftrightarrow\left(x^2-1\right)\left(x^4+x^2+1\right)=0\)

\(\Leftrightarrow x^2-1=0\) (Vì \(x^4+x^2+1>0\))

\(\Leftrightarrow x=\pm1\)

\(d,x^6-1=0\\ \Leftrightarrow\left(x^2\right)^3-1^3=0\\ \Leftrightarrow\left(x^2-1\right)\left(x^4+x^2+1\right)=0\\ \Leftrightarrow\left(x-1\right)\left(x+1\right)\left(x^4+x^2+1\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x-1=0\\x+1=0\\x^4+x^2+1=0\left(Vô.lí,vì:x^4\ge0;x^2\ge0,\forall x\in R\right)\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=1\\x=-1\end{matrix}\right.\\ c,\left(x^3+8\right)-\left(x+2\right)\left(x-4\right)=0\\ \Leftrightarrow\left(x^3+8\right)-\left(x^2-2x-8\right)=0\\ \Leftrightarrow x^3-x^2+2x+16=0\\ \Leftrightarrow x^3+2x^2-3x^2-6x+8x+16=0\\ \Leftrightarrow x^2\left(x+2\right)-3x\left(x+2\right)+8\left(x+2\right)=0\\ \Leftrightarrow\left(x^2-3x+8\right)\left(x+2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}x^2-3x+8=0\left(Vô.lí\right)\\x+2=0\end{matrix}\right.\Leftrightarrow x=-2\)

c)(x^3+ 8) - (x + 2)(x - 4) = 0
<=> x^3 -x^2 + 2x +8 + 8 = 0
<=> x^3 -x^2 + 2x + 16 = 0
<=> (x+2)(x^2-3x+8) = 0
=> x = -2