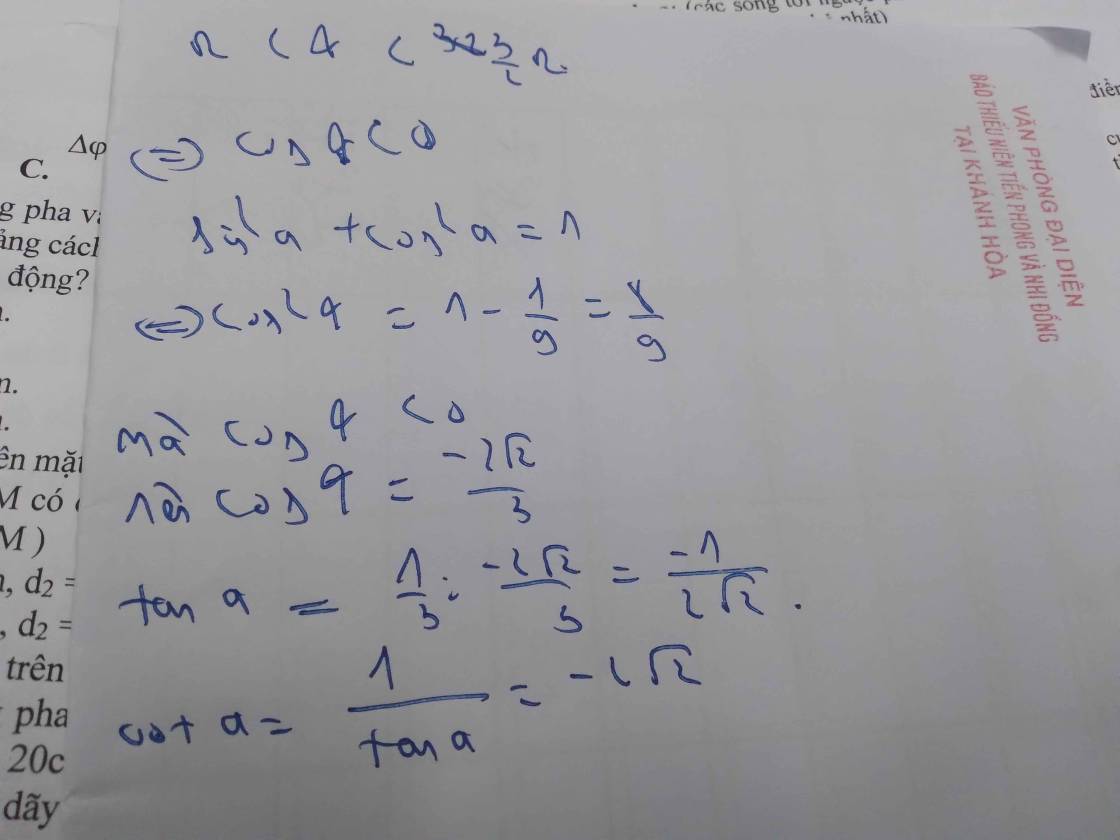tính các giá trị lượng giác của góc anpha=-30 độ

Những câu hỏi liên quan
cho tam giác ABC đều cạnh 4 cm , đường cao AH . Tính số đo độ dài các cạnh AB , AH , BH của tam giác ABH , từ đó tính tỉ số lượng giác của cá góc a ( anpha) , b
Sử dụng \({15^0} = {45^0} - {30^0}\), hãy tính các giá trị lượng giác của góc \({15^0}\).
Ta có:
\(\cos {15^0} = \cos \left( {{{45}^0} - {{30}^0}} \right) = \cos {45^0}\cos {30^0} + \sin {45^0}\sin {30^0} = \frac{{\sqrt 2 }}{2}.\frac{{\sqrt 3 }}{2} + \frac{{\sqrt 2 }}{2}.\frac{1}{2} = \frac{{\sqrt 6 + \sqrt 2 }}{4}\)
\(\sin {15^0} = \sin \left( {{{45}^0} - {{30}^0}} \right) = \sin {45^0}\cos {30^0} - \cos {45^0}\sin {30^0} = \frac{{\sqrt 2 }}{2}.\frac{{\sqrt 3 }}{2} - \frac{{\sqrt 2 }}{2}.\frac{1}{2} = \frac{{\sqrt 6 - \sqrt 2 }}{4}\)
\(\tan {15^0} = \tan \left( {{{45}^0} - {{30}^0}} \right) = \frac{{\tan {{45}^0} - \tan {{30}^0}}}{{1 + \tan {{45}^0}\tan {{30}^0}}} = \frac{{1 - \frac{{\sqrt 3 }}{3}}}{{1 + \frac{{\sqrt 3 }}{3}}} = 2 - \sqrt 3 \)
\(\cot {15^0} = \frac{1}{{\tan {{15}^0}}} = \frac{1}{{2 - \sqrt 3 }}\)
Đúng 0
Bình luận (0)
Xét dấu các giá trị lượng giác của góc lượng giác \(\alpha = - 30^\circ \)
\(\begin{array}{l}\cos \left( { - 30^\circ } \right) = \frac{{\sqrt 3 }}{2} > 0\\\sin \left( { - 30^\circ } \right) = - \frac{1}{2} < 0\\\tan \left( { - 30^\circ } \right) = - \frac{{\sqrt 3 }}{3} < 0\\\cot \left( { - 30^\circ } \right) = - \sqrt 3 < 0\end{array}\)
Đúng 0
Bình luận (0)
Tính giá trị lượng giác của các góc sau đây:
a) 120 độ
b) 150 độ
c) 180 độ
a) \(\left\{{}\begin{matrix}sin120^o=\dfrac{\sqrt{3}}{2}\\cos120^o=-\dfrac{1}{2}\\tan120^o=-\sqrt{3}\\cot120^o=-\dfrac{\sqrt{3}}{3}\end{matrix}\right.\)
b) \(\left\{{}\begin{matrix}sin150^o=\dfrac{1}{2}\\cos150^o=-\dfrac{\sqrt{3}}{2}\\tan150^o=-\dfrac{\sqrt{3}}{3}\\cot150^o=-\sqrt{3}\end{matrix}\right.\)
c) \(\left\{{}\begin{matrix}sin180^o=0\\cos180^o=-1\\tan180^o=0\\cot180^o\left(\varnothing\right)\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Cho cos anpha = \(\frac{2}{3}\)tính các tỉ số lượng giác góc anpha
+\(cos^2\alpha+sin^2\alpha=1\Rightarrow sin^2\alpha=1-cos^2\alpha=1-\frac{4}{9}=\frac{5}{6}\Rightarrow sin\alpha=\pm\sqrt{\frac{5}{6}}\)
+\(tan\alpha=\frac{sin\alpha}{cos\alpha}=\frac{\pm\sqrt{\frac{5}{6}}}{\frac{2}{3}}\)
+\(cotg\alpha=\frac{1}{tan\alpha}=\frac{\frac{2}{3}}{\pm\sqrt{\frac{5}{6}}}\)
Đúng 0
Bình luận (0)
cho sin anpha= 1/3với π<anpha<3π/2 .tính các giá trị lượng giác.
mọi người ơi giúp mình giúp giải bt này với ạ
Một hệ gồm hai vật có khôi lượng m1=1kg và m2=2kg chuyển động thẳng đều với tốc độ lần lượt là 3m/s và 2m/s theo hai hướng hợp nhau góc anpha 60 độ. Độ lớn của động lượng có giá trị là
Độ lớn động lượng:
\(p=\sqrt{p_1^2+p_2^2+2p_1p_2cos60^0}\)
\(\Leftrightarrow p=\sqrt{\left(1\cdot3\right)^2+\left(2\cdot2\right)^2+2\cdot3\cdot1\cdot2\cdot2\cdot cos60^0}\)
\(\Leftrightarrow p=\sqrt{37}\left(kg\cdot\dfrac{m}{s}\right)\)
Đúng 2
Bình luận (0)
Xác định số ảnh và vẽ vị trí các ảnh của nguồn sáng điểm S trong hệ Gương, gồm hai gương G1 và G2 tạo với nhau góc anpha, trong đó S nằm trên tia phân giác của góc anpha giữa hai gương. Cụ thể:
a. Anpha = 120 độ
b. Anpha = 90 độ
c. Anpha = 60 độ
Cho biết \(\sin {30^o} = \frac{1}{2};\sin {60^o} = \frac{{\sqrt 3 }}{2};\tan {45^o} = 1.\) Sử dụng mối liên hệ giữa các giá trị lượng giác của hai góc bù nhau, phụ nhau để tính giá trị của \(E = 2\cos {30^o} + \sin {150^o} + \tan {135^o}.\)
Ta có:
\(\begin{array}{l}\cos {30^o} = \sin \left( {{{90}^o} - {{30}^o}} \right) = \sin {60^o} = \frac{{\sqrt 3 }}{2};\\\sin {150^o} = \sin \left( {{{180}^o} - {{150}^o}} \right) = \sin {30^o} = \frac{1}{2};\\\tan {135^o} = - \tan \left( {{{180}^o} - {{135}^o}} \right) = - \tan {45^o} = - 1\end{array}\)
\( \Rightarrow E = 2.\frac{{\sqrt 3 }}{2} + \frac{1}{2} - 1 = \sqrt 3 - \frac{1}{2}.\)
Đúng 0
Bình luận (0)