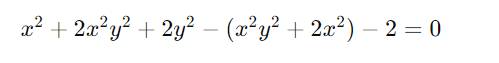Cho 2x2+2y2=5xy và 0<x<y .Tính giá trị cưa E =x+y/x-y

Những câu hỏi liên quan
Cho hai đa thức
N
5
x
2
-
3
x
y
,
M
5
x
y
+
2
x
2
-
2
y
2
.
Tìm đa thức P biết P + N M A.
-
3
x
2
+
8
x
y
-...
Đọc tiếp
Cho hai đa thức N = 5 x 2 - 3 x y , M = 5 x y + 2 x 2 - 2 y 2 . Tìm đa thức P biết P + N = M
A. - 3 x 2 + 8 x y - 2 y 2
B. 7 x 2 + 2 x y - 2 y 2
C. - 3 x 2 - 8 x y + 2 y 2
D. - x 2 + 8 x y + 2 y 2
Chọn A
Ta có P + N = M ⇒ P = M - N
= 5xy + 2x2- 2y2-5x2+ 3xy
= -3x2+ 8xy - 2y2
Đúng 0
Bình luận (0)
1, Phân tích đa thức thành nhân tử:
a,f(x;y)=2x2+5xy+2y2-5x-4y+2
Tìm tất cả các bộ số nguyên dương thỏa mãn phương trình : 2x2 + 2y2 − 5xy + x − 2y + 3 = 0
giúp mình với, mình đang cần gấp
\(2x^2+2y^2-5xy+x-2y+3=0\)
\(\Leftrightarrow\left(x-2y\right)\left(2x-y\right)+x-2y+3=0\)
\(\Leftrightarrow\left(x-2y\right)\left(2x-y+1\right)=-3\)
| x-2y | -3 | -1 | 1 | 3 |
| 2x-y+1 | 1 | 3 | -3 | -1 |
| x | 1 | 5/3 | -3 | -7/3 |
| y | 2 | 4/3 | -2 | -8/3 |
Vậy \(\left(x;y\right)=\left(1;2\right)\) là bộ nghiệm nguyên dương duy nhất
Đúng 1
Bình luận (0)
Cho đường tròn (C) có phương trình
2
x
2
+
2
y
2
−
3
x
+
7
y
+
1
0
. Khi đó đường tròn có tâm I và bán kính R với A.
3
4
;
−
7
4
,
...
Đọc tiếp
Cho đường tròn (C) có phương trình 2 x 2 + 2 y 2 − 3 x + 7 y + 1 = 0 . Khi đó đường tròn có tâm I và bán kính R với
A. 3 4 ; − 7 4 , R = 5 2 2
B. I − 3 4 ; 7 4 , R = 2 2
C. I 3 4 ; − 7 4 , R = 1
D. I 3 2 ; − 7 2 , R = 15
Ta có 2 x 2 + 2 y 2 − 3 x + 7 y + 1 = 0 ⇔ x 2 + y 2 − 3 2 x + 7 2 y + 1 2 = 0
⟺ ( x − 3 / 4 ) 2 + ( y + 7 / 4 ) 2 = 25 / 8 nên đường tròn có tâm I 3 4 ; − 7 4 và bán kính I 3 4 ; − 7 4
ĐÁP ÁN A
Đúng 0
Bình luận (0)
Giải phương trình nghiệm nguyên:
3x2 + 5xy - 8x -2y2 - 9y - 4 = 0
Lời giải:
PT $\Leftrightarrow 3x^2+x(5y-8)-(2y^2+9y+4)=0$
Coi đây là pt bậc 2 ẩn $x$. Để pt có nghiệm nguyên thì:
$\Delta=(5y-8)^2+12(2y^2+9y+4)=t^2$ với $t\in\mathbb{N}$)
$\Leftrightarrow 49y^2+28y+112=t^2$
$\Leftrightarrow (7y+2)^2+108=t^2$
$\Leftrightarrow 108=(t-7y-2)(t+7y+2)$
Đến đây là dạng phương trình tích đơn giản rồi. Bạn chỉ cần xét TH. Lưu ý rằng $t+7y+2>0$ và $t-7y-2, t+7y+2$ có cùng tính chẵn lẻ.
Đúng 0
Bình luận (0)
Phân tích thành nhân tử
a)x2+2y2-3xy+x-2y
b)x2+4xy+2x+3y2+6y
C)2x2+5x-12y2+12y-3-10xy
d)3x2-5xy+2y2+4x-4y
Những bài này làm như thế nào vậy có cần công thức hay mẹo gì ko hay là phải khéo léo mới làm được????
Ko hiểu thì kb vs mik
mik chỉ thêm cho
Đúng 0
Bình luận (0)
Tìm x ,y thỏa mãn: x2 + 2x2y2 + 2y2 - (x2y2 + 2x2) - 2 = 0 .
cac ban giup minh voi roi minh tick cho
Bạn vui lòng viết đề đầy đủ, và gõ bằng công thức toán để được hỗ trợ tốt hơn.
Đúng 2
Bình luận (0)
cho các số dương x,y,z thỏa mãn x+y+z=1 tìm min của biểu thức
P=√(2x2+xy+2y2) +√(2y2+yz+2z2)+ √(2z2+xz+2x2)
Ta có: \(2x^2+xy+2y^2=\dfrac{3}{2}\left(x^2+y^2\right)+\dfrac{1}{2}\left(x^2+2xy+y^2\right)=\dfrac{3}{2}\left(x^2+y^2\right)+\dfrac{1}{2}\left(x+y\right)^2\)
Theo BĐT Bunhacopxky: \(\left(x^2+y^2\right)\left(1+1\right)\ge\left(x+y\right)^2\Rightarrow\dfrac{3}{2}\left(x^2+y^2\right)\ge\dfrac{3}{4}\left(x+y\right)^2\\ \Rightarrow2x^2+xy+2y^2=\dfrac{3}{2}\left(x^2+y^2\right)+\dfrac{1}{2}\left(x+y\right)^2\ge\dfrac{5}{4}\left(x+y\right)^2\\ \Rightarrow\sqrt{2x^2+xy+2y^2}\ge\dfrac{\sqrt{5}}{2}\left(x+y\right)\)
Chứng minh tương tự:
\(\sqrt{2y^2+yz+2z^2}\ge\dfrac{\sqrt{5}}{2}\left(y+z\right)\\ \sqrt{2z^2+xz+2x^2}\ge\dfrac{\sqrt{5}}{2}\left(x+z\right)\)
Cộng vế theo vế, ta được: \(P\ge\sqrt{5}\left(x+y+z\right)=\sqrt{5}\cdot1=\sqrt{5}\)
Dấu "=" \(\Leftrightarrow x=y=z=\dfrac{1}{3}\)
Đúng 2
Bình luận (0)
Bạn tham khảo nhé
https://hoc24.vn/cau-hoi/cho-cac-so-duong-xyz-thoa-man-xyz1cmrcan2x2xy2y2can2y2yz2z2can2z2zx2x2can5.182722154737
Đúng 1
Bình luận (0)
Giải hệ pt:hệ bậc 2-2 ẩn
x2+2x-2y2=0
y2+2y-2x2=0
\(\left\{{}\begin{matrix}x^2+2x-2y^2=0\\y^2+2y-2x^2=0\end{matrix}\right.\)\(\left(1\right)-\left(2\right)\Rightarrow x^2+2x-2y^2-y^2-2y+2x^2=0\)
\(\Leftrightarrow\left(x-y\right)\left(3x+3y+2\right)=0\Leftrightarrow\left(x-y\right)3\left(x+y+\dfrac{2}{3}\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x-y=0\\x+y+\dfrac{2}{3}=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=y\left(2\right)\\x=-\dfrac{2}{3}-y\left(3\right)\end{matrix}\right.\)
\(thế\left(2\right)và\left(3\right)lên-hệ-pt-rồi-giải\)
Đúng 2
Bình luận (0)