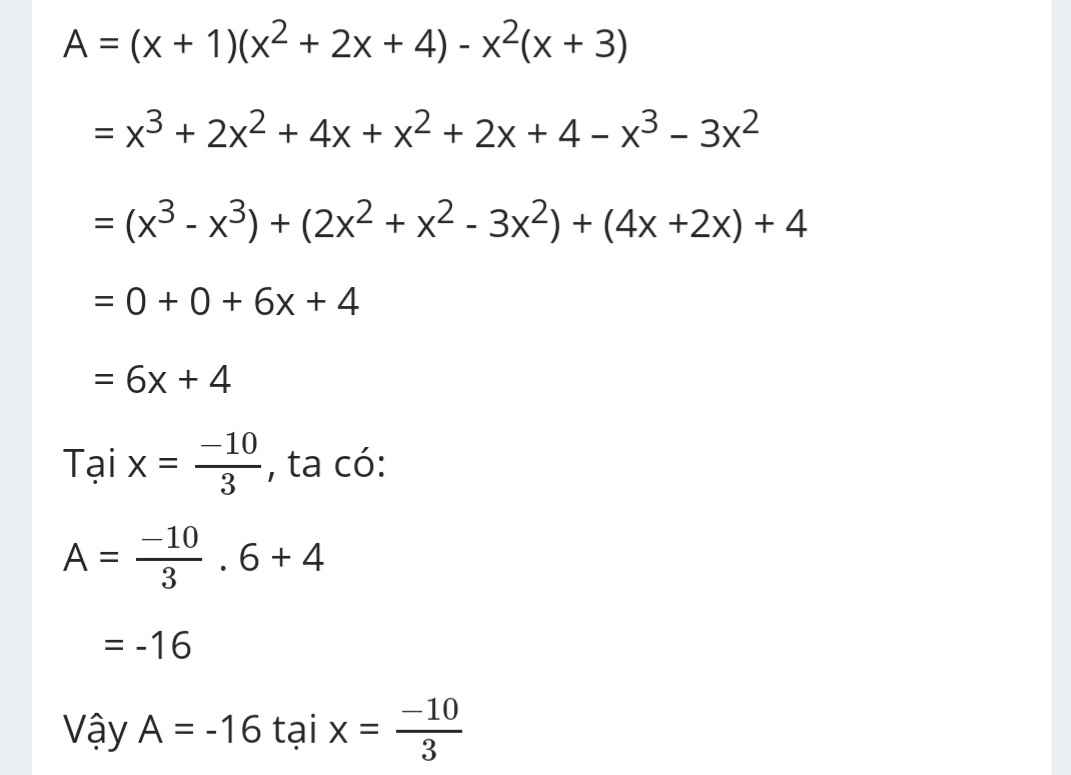a) \(A=3\left(x+5\right)+x^2\)

Thay x = 1 vào A, ta được:

\(A=3\left(1+5\right)+1^2\)

\(A=3.6+1\)

\(A=19\)

b) \(B=3x\left(x+2\right)-x\left(x+1\right)\)

Thay x = -1 vào B, ta được:

\(B=3.\left(-1\right)\left(-1+2\right)-\left(-1\right)\left(-1+1\right)\)

\(B=-3-0\)

\(B=-3\)

c) \(C=7x\left(x-5\right)+3\left(x-2\right)\)

Thay x = 0 vào C, ta được:

\(C=7.0.\left(0-5\right)+3.\left(0-2\right)\)

\(C=0+3.\left(-2\right)\)

\(C=-6\)

d) \(D=-2x\left(x+1\right)+4\left(x+2\right)\)

Thay x = -1 vào D, ta được:

\(D=-2\left(-1\right)\left(-1+1\right)+4\left(-1+2\right)\)

\(D=0+4\)

\(D=4\)

e) \(E=x^2-x+2x\left(x+3\right)\)

Thay x = 2 vào E, ta được:

\(E=2^2-2+2.2\left(2+3\right)\)

\(E=4-2+4.5\)

\(E=22\)

f) \(F=5-4x\left(x-2\right)\)

Thay x = -1 vào F, ta được:

\(F=5-4.\left(-1\right)\left(-1-2\right)\)

\(F=5-12\)

\(F=-7\)

g) \(G=x\left(x-5\right)-2x\left(x+1\right)+x^2\)

Thay x = -2 vào G, ta được:

\(G=-2\left(-2-5\right)-2.\left(-2\right)\left(-2+1\right)+\left(-2\right)^2\)

\(G=14-4+4\)

\(G=14\)

h) \(H=x\left(7x+2\right)-5x\left(x+3\right)\)

Thay x = 1 vào H, ta được:

\(H=1\left(7.1+2\right)-5.1\left(1+3\right)\)

\(H=9-20\)

\(H=-11\)

i) \(I=3x^2-2x\left(x-5\right)+x\left(x-7\right)\)

Thay x = 10 vào I, ta được:

\(I=3.10^2-2.10\left(10-5\right)+10.\left(10-7\right)\)

\(I=300-100+30\)

\(I=230\)

thu gọn rồi mới tính bạn nha

a) Thay x=1:

\(9.1^2+12.1+49=70\)

b) Thay x=-2 và y=3:

\(25.\left(-2\right)^2-10\left(-2\right).3+3^2\)\(=169\)

c)Thay x=-10:

\(\left(-10\right)^3+15\left(-10\right)^2+75\left(-10\right)+125=-125\)

d) Thay x=13:

\(13^3-9.13^2+27.13-27=1000\)

e) Thay x=-2:

\(\left(-2-1\right)^3-4\left(-2\right)\left(-2+1\right)\left(-2-1\right)+3\left(-2-1\right)\left[\left(-2\right)^2-2+1\right]\)=-30

f) Thay x=1:

\(\left(1-1\right)\left(1-2\right)\left(1+1+1\right)\left(4+2+1\right)=0\)

\(9x^2+12x+49=\left(9x^2+12x+4\right)+45=\left(3x+2\right)^2+45=5^2+45=25+45=70\)

\(25x^2-10xy+y^2=\left(5x-y\right)^2=\left(-13\right)^2=169\)

\(x^3+15x^2+75x+125=\left(x^3+5x^2\right)+\left(10x^2+50x\right)+\left(25x+125\right)=x^2\left(x+5\right)+10x\left(x+5\right)+25\left(x+5\right)=\left(x+5\right)^2\left(x+5\right)=\left(x+5\right)^3=-125\)

\(x^3-9x^2+27x-27=\left(x^3-3x^2\right)-\left(6x^3-18x\right)+\left(9x-27\right)=x^2\left(x-3\right)-6x\left(x-3\right)+9\left(x-3\right)=\left(x-3\right)^3=1000\)

\(x=1\Rightarrow x-1=0\Rightarrow\left(x-1\right)\left(x-2\right)\left(1+x+x^2\right)\left(4+2x+x^2\right)=0\)

b: Ta có: \(x^3-9x^2+27x-27\)

\(=\left(x-3\right)^3\)

\(=\left(-7\right)^3=-343\)

c: Ta có: \(\dfrac{x^3-1}{x^2+1}\)

\(=\dfrac{6^3-1}{6^2+1}=\dfrac{215}{37}\)

Giải:

a) \(B=3x\left(x+2\right)-x\left(x+1\right)\)

Tại x = -1, ta được:

\(B=3\left(-1\right)\left(-1+2\right)-\left(-1\right)\left(-1+1\right)\)

\(\Leftrightarrow B=-3-0=-3\)

b) \(C=7x\left(x-5\right)+3\left(x-2\right)\)

Tại x = 0, ta được:

\(C=7.0\left(0-5\right)+3\left(0-2\right)\)

\(\Leftrightarrow C=0+\left(-6\right)=-6\)

c) \(D=-2x\left(x+1\right)+4\left(x+2\right)\)

Tại x = -1, ta được:

\(D=-2\left(-1\right)\left(-1+1\right)+4\left(-1+2\right)\)

\(\Leftrightarrow D=0+4=4\)

d) \(E=x\left(x-5\right)-2x\left(x+1\right)+x^2\)

Tại x = -2, ta được:

\(E=-2\left(-2-5\right)-2\left(-2\right)\left(-2+1\right)+\left(-2\right)^2\)

\(\Leftrightarrow E=14-4+4=14\)

e) \(F=x\left(7x+2\right)-5x\left(x+3\right)\)

Tại x = 1, ta được:

\(F=1\left(7.1+2\right)-5.1\left(1+3\right)\)

\(F=9-20=-11\)

Vậy ...

\(B=3x\left(x+2\right)-x\left(x+1\right)\)

\(B=3x^2+6x-x^2-x\)

\(B=2x^2+5x\)

\(B=x\left(2x+5\right)\)

Tại x = -1 ta có :

\(B=\left(-1\right)\left[2.\left(-1\right)+5\right]=\left(-1\right).3=-3\)

\(C=7x\left(x-5\right)+3\left(x-2\right)\)

\(C=7x^2-35x+3x-6\)

\(C=7x^2-32x-6\)

Tại x=0 ta có :

\(C=7.0-32.0+6=6\)

\(D=-2x\left(x+1\right)+4\left(x+2\right)\)

\(D=-2x^2-2x+4x+8\)

\(D=-2x^2+2x+8\)

\(D=-2\left(x^2-x-4\right)\)

Tại x = -1 ta có :

\(D=-2.\left[\left(-1\right)^2-\left(-1\right)-4\right]=4\)

\(E=x\left(x-5\right)-2x\left(x+1\right)+x^2\)

\(E=x^2-5x-2x^2-2x+x^2\)

\(E=-7x\)

Tại x = -2 ta có :

\(E=-7\left(-2\right)=14\)

\(F=x\left(7x+2\right)-5x\left(x+3\right)\)

\(F=7x^2+2x-5x^2-15x\)

\(F=2x^2-13x=x\left(2x-13\right)\)

Tại x= 1 ta có :

\(F=1.\left(2.1-13\right)=-11\)

a, bạn xem lại đề 

b, \(\frac{x^3-1}{x^2-1}=\frac{\left(x-1\right)\left(x^2+x+1\right)}{\left(x-1\right)\left(x+1\right)}=\frac{x^2+x+1}{x+1}\)

Thay x = 6 ta được : \(=\frac{36+6+1}{6+1}=\frac{43}{7}\)

c, \(\frac{x^2-2x+1}{x^3-1}+\frac{x^2-1}{\left(x-1\right)^2}=\frac{x-1}{x^2+x+1}+\frac{x+1}{x-1}\)

\(=\frac{x^2-1+x^3+x^2+x+x^2+x+1}{x^3-1}=\frac{x^3+3x^2+2x}{x^3-1}=\frac{x\left(x^2+3x+2\right)}{x^3-1}\)

giúp mik vs mik cần gấp

\(b=x^6+x^5+x^4+x^3+x+17\)

\(b=x^6+x^5+x^4+x^3+x+1+16\)

\(b=\left(x^6+x^5\right)+\left(x^4+x^3\right)+\left(x+1\right)+16\)

\(b=x^5\left(x+1\right)+x^3\left(x+1\right)+1\left(x+1\right)+16\)

\(b=\left(x^5+x^3+1\right)\left(x+1\right)+16\)

\(b=10\left(9^5+9^3+1\right)+16\)

\(c=\left(x+3\right)\left(x-2\right)-x\left(x+1\right)\)

\(c=\left(x^2-2x+3x-6\right)-\left(x^2+x\right)\)

\(c=\left(x^2+x-6\right)-\left(x^2+x\right)\)

\(c=x^2+x-6-x^2-x=-6\)

nên biểu thức không phụ thuộc vào biến

\(x=bn\) cx đc

\(d) (x+1)^3-6y(x+1)^2+12y^2(x+1)-8y^3\)

\(=\left(x+1\right)^3-3\cdot\left(x+1\right)^2\cdot2y+3\cdot\left(x+1\right)\cdot\left(2y\right)^2-\left(2y\right)^3\)

\(=\left[\left(x+1\right)-2y\right]^3\)

\(=\left(x-2y+1\right)^3\)     (1)

Thay \(x=2;y=1,5\) vào (1), ta được:

\(\left(2-2\cdot1,5+1\right)^3\)

\(=\left(2-3+1\right)^3\)

\(=0\)

 \(---\)

\(e,\left(x-2\right)^3+3y\left(x-2\right)^2+3y^2\left(x-2\right)+y^3\) (sửa đề)

\(=\left(x-2\right)^3+3\cdot\left(x-2\right)^2\cdot y+3\cdot\left(x-2\right)\cdot y^2+y^3\)

\(=\left[\left(x-2\right)+y\right]^3\)

\(=\left(x+y-2\right)^3\)   (2)

Thay \(x+y=7\) vào (2), ta được:

\(\left(7-2\right)^3=5^3=125\)

#\(Toru\)

Lời giải:
Áp dụng hằng đẳng thức đáng nhớ:

d. $=[(x+1)-(2y)]^3=(2+1-2.1,5)^3=(3-3)^3=0$

e. Sửa đề: $(x-2)^3+3y(x-2)^2+3y^2(x-2)+y^3$

$=(x-2+y)^3=(x+y-2)^3=(7-2)^3=5^3=125$