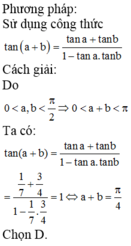cho 2 góc nhọn a và b với tana=1/2, tanb=1/3. tính a+b

Những câu hỏi liên quan
Cho A: B; C là các góc nhọn và tanA 1/2, tanB 1/5, tanC 1/8,. Tổng A + B + C bằng
Đọc tiếp
Cho A: B; C là các góc nhọn và tanA = 1/2, tanB = 1/5, tanC = 1/8,. Tổng A + B + C bằng
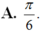
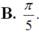
![]()
Chọn C.
Áp dụng công thức cộng ta có:
suy ra 
Đúng 0
Bình luận (0)
Cho hai góc nhọn a và b thỏa mãn
t
a
n
a
1
7
và
tan
b
3
4
. Tính a + b A.
π
3
B.
2
π
3
C.
π
6
D.
π
4
Đọc tiếp
Cho hai góc nhọn a và b thỏa mãn t a n a = 1 7 và tan b = 3 4 . Tính a + b
A. π 3
B. 2 π 3
C. π 6
D. π 4
cho tam giác abc có 3 góc nhọn. Vẽ đường cáo AD, BE, CF cắt nhau tại H. Chứng minh:
a) \(0< cos^2A+cos^2B+cos^2C< 1\)
b)\(2< sin^2A+sin^2B+sin^2C< 3\)
c)sinA + sinB + sinC < 2( cosA + cosB + cosC)
d)sinB . cosC + sinC . cosB = sinA
e)tanA + tanB + tanC = tanA . tanB . tanC
Tính giá trị lượng giác của biểu thức : tana+ tanb, tana,tanb , khi 0<a, b<π/2,a+b= π/4, và tana* tanb=3-2 căn 2. Từ đó tính a, b
Vì 0<a,b<\(\frac{\pi}{2}\)nên tana,tanb>0 ⇒ tana+tanb>0
ta có tan(a+b)=\(\frac{tana+tanb}{1-tana.tanb}\) ⇔tana+tanb=tan(a+b)(1-3+2\(\sqrt{2}\))
⇔tana+tanb=tan(\(\frac{\pi}{4}\)).(-2+2\(\sqrt{2}\))=-2+2\(\sqrt{2}\)(thỏa)
ta có \(\left\{{}\begin{matrix}tana.tanb=3-2\sqrt{2}\\tana+tanb=-2+2\sqrt{2}\end{matrix}\right.\)
áp đụng hệ thức Vi-et đảo ta có: tana và tanb là hai nghiệm của phương trình: X2+(2-2\(\sqrt{2}\))X+3-2\(\sqrt{2}\)=0
bấm máy giải phương trình trên ta được 2 nghiệm x1,x2
Vậy (tana;tanb)=(x1;x2) hoặc (x2;x1) và tana.tanb=3-2\(\sqrt{2}\)
Đúng 1
Bình luận (0)
Cho A, B, C là 3 góc nhọn của tam giác ABC. Chứng minh:
a) tanA+tanB+tanCtanA.tanB.tanC
Tính min P với PtanA+tanB+tanC
b) tanleft(dfrac{A}{2}right).tanleft(dfrac{B}{2}right)+tanleft(dfrac{B}{2}right)tanleft(dfrac{C}{2}right)+tanleft(dfrac{C}{2}right).tanleft(dfrac{A}{2}right)1
Tìm min T với Ttanleft(dfrac{A}{2}right)+tanleft(dfrac{B}{2}right)+tanleft(dfrac{C}{2}right)
Đọc tiếp
Cho A, B, C là 3 góc nhọn của tam giác ABC. Chứng minh:
a) \(tanA+tanB+tanC=tanA.tanB.tanC\)
Tính min P với \(P=tanA+tanB+tanC\)
b) \(tan\left(\dfrac{A}{2}\right).tan\left(\dfrac{B}{2}\right)+tan\left(\dfrac{B}{2}\right)tan\left(\dfrac{C}{2}\right)+tan\left(\dfrac{C}{2}\right).tan\left(\dfrac{A}{2}\right)=1\)
Tìm min T với \(T=tan\left(\dfrac{A}{2}\right)+tan\left(\dfrac{B}{2}\right)+tan\left(\dfrac{C}{2}\right)\)
Câu a)
Ta sử dụng 2 công thức:
\(\bullet \tan (180-\alpha)=-\tan \alpha\)
\(\bullet \tan (\alpha+\beta)=\frac{\tan \alpha+\tan \beta}{1-\tan \alpha.\tan \beta}\)
Áp dụng vào bài toán:
\(\text{VT}=\tan A+\tan B+\tan C=\tan A+\tan B+\tan (180-A-B)\)
\(=\tan A+\tan B-\tan (A+B)=\tan A+\tan B-\frac{\tan A+\tan B}{1-\tan A.\tan B}\)
\(=(\tan A+\tan B)\left(1+\frac{1}{1-\tan A.\tan B}\right)=(\tan A+\tan B).\frac{-\tan A.\tan B}{1-\tan A.\tan B}\)
\(=-\tan A.\tan B.\frac{\tan A+\tan B}{1-\tan A.\tan B}=-\tan A.\tan B.\tan (A+B)\)
\(=\tan A.\tan B.\tan (180-A-B)\)
\(=\tan A.\tan B.\tan C=\text{VP}\)
Do đó ta có đpcm
Tam giác $ABC$ có ba góc nhọn nên \(\tan A, \tan B, \tan C>0\)
Áp dụng BĐT Cauchy ta có:
\(P=\tan A+\tan B+\tan C\geq 3\sqrt[3]{\tan A.\tan B.\tan C}\)
\(\Leftrightarrow P=\tan A+\tan B+\tan C\geq 3\sqrt[3]{\tan A+\tan B+\tan C}\)
\(\Rightarrow P\geq 3\sqrt[3]{P}\)
\(\Rightarrow P^3\geq 27P\Leftrightarrow P(P^2-27)\geq 0\)
\(\Rightarrow P^2-27\geq 0\Rightarrow P\geq 3\sqrt{3}\)
Vậy \(P_{\min}=3\sqrt{3}\). Dấu bằng xảy ra khi \(\angle A=\angle B=\angle C=60^0\)
Đúng 0
Bình luận (0)
Câu b)
Ta sử dụng 2 công thức chính:
\(\bullet \tan (\alpha+\beta)=\frac{\tan \alpha+\tan \beta}{1-\tan \alpha.\tan \beta}\)
\(\bullet \tan (90-\alpha)=\frac{1}{\tan \alpha}\)
Áp dụng vào bài toán:
\(\text{VT}=\tan \frac{A}{2}.\tan \frac{B}{2}+\tan \frac{B}{2}.\tan \frac{C}{2}+\tan \frac{C}{2}.\tan \frac{A}{2}\)
\(=\tan \frac{A}{2}.\tan \frac{B}{2}+\tan \frac{C}{2}(\tan \frac{A}{2}+\tan \frac{B}{2})\)
\(=\tan \frac{A}{2}.\tan \frac{B}{2}+\tan (90-\frac{A+B}{2})(\tan \frac{A}{2}+\tan \frac{B}{2})\)
\(=\tan \frac{A}{2}.\tan \frac{B}{2}+\frac{\tan \frac{A}{2}+\tan \frac{B}{2}}{\tan (\frac{A+B}{2})}\)
\(=\tan \frac{A}{2}.\tan \frac{B}{2}+\frac{\tan \frac{A}{2}+\tan \frac{B}{2}}{\frac{\tan \frac{A}{2}+\tan \frac{B}{2}}{1-\tan \frac{A}{2}.\tan \frac{B}{2}}}\)
\(=\tan \frac{A}{2}.\tan \frac{B}{2}+1-\tan \frac{A}{2}.\tan \frac{B}{2}=1=\text{VP}\)
Ta có đpcm.
Cũng giống phần a, ta biết do ABC là tam giác nhọn nên
\(\tan A, \tan B, \tan C>0\)
Đặt \(\tan A=x, \tan B=y, \tan C=z\). Ta có: \(xy+yz+xz=1\)
Và \(T=x+y+z\)
\(\Rightarrow T^2=x^2+y^2+z^2+2(xy+yz+xz)\)
Theo hệ quả quen thuộc của BĐT Cauchy:
\(x^2+y^2+z^2\geq xy+yz+xz\)
\(\Rightarrow T^2\geq 3(xy+yz+xz)=3\)
\(\Rightarrow T\geq \sqrt{3}\Leftrightarrow T_{\min}=\sqrt{3}\)
Dấu bằng xảy ra khi \(x=y=z=\frac{1}{\sqrt{3}}\Leftrightarrow \angle A=\angle B=\angle C=60^0\)
Đúng 0
Bình luận (0)
Câu a)
Ta sử dụng 2 công thức:
∙tan(180−α)=−tanα∙tan(180−α)=−tanα
∙tan(α+β)=tanα+tanβ1−tanα.tanβ∙tan(α+β)=tanα+tanβ1−tanα.tanβ
Áp dụng vào bài toán:
VT=tanA+tanB+tanC=tanA+tanB+tan(180−A−B)VT=tanA+tanB+tanC=tanA+tanB+tan(180−A−B)
=tanA+tanB−tan(A+B)=tanA+tanB−tanA+tanB1−tanA.tanB=tanA+tanB−tan(A+B)=tanA+tanB−tanA+tanB1−tanA.tanB
=(tanA+tanB)(1+11−tanA.tanB)=(tanA+tanB).−tanA.tanB1−tanA.tanB=(tanA+tanB)(1+11−tanA.tanB)=(tanA+tanB).−tanA.tanB1−tanA.tanB
=−tanA.tanB.tanA+tanB1−tanA.tanB=−tanA.tanB.tan(A+B)=−tanA.tanB.tanA+tanB1−tanA.tanB=−tanA.tanB.tan(A+B)
=tanA.tanB.tan(180−A−B)=tanA.tanB.tan(180−A−B)
=tanA.tanB.tanC=VP=tanA.tanB.tanC=VP
Do đó ta có đpcm
Tam giác ABCABC có ba góc nhọn nên tanA,tanB,tanC>0tanA,tanB,tanC>0
Áp dụng BĐT Cauchy ta có:
P=tanA+tanB+tanC≥33√tanA.tanB.tanCP=tanA+tanB+tanC≥3tanA.tanB.tanC3
⇔P=tanA+tanB+tanC≥33√tanA+tanB+tanC⇔P=tanA+tanB+tanC≥3tanA+tanB+tanC3
⇒P≥33√P⇒P≥3P3
⇒P3≥27P⇔P(P2−27)≥0⇒P3≥27P⇔P(P2−27)≥0
⇒P2−27≥0⇒P≥3√3⇒P2−27≥0⇒P≥33
Vậy Pmin=3√3Pmin=33. Dấu bằng xảy ra khi ∠A=∠B=∠C=600
cho tana=1/12 tanb=2/5 tanc=1/3. Chứng minh a+b+c=45 độ
MN giuwps mk vs ạ
cho góc nhọn a . tính B = sina + cosa biết tana + cota = 3
Cho a + b = \(\dfrac{\Pi}{4}\). Tính: \(M=\left(1+tana\right)\left(1+tanb\right)\).
\(1=tan\left(\dfrac{\pi}{4}\right)=tan\left(a+b\right)=\dfrac{tana+tanb}{1-tana.tanb}\)
\(\Rightarrow tana+tanb=1-tana.tanb\)
\(\Rightarrow tana+tanb+tana.tanb=1\)
Do đó:
\(M=1+tana+tanb+tana.tanb=1+1=2\)
Đúng 0
Bình luận (0)
Cho \(\Delta ABC\) có ba góc nhọn. CMR: \(\dfrac{tanA}{tan^3B}+\dfrac{tanB}{tan^3C}+\dfrac{tanC}{tan^3A}\ge1\)
Ta có:
\(\dfrac{tanA}{tan^3B}=\dfrac{tanA}{tanB}.\dfrac{1}{tan^2B}=\dfrac{\dfrac{sinA}{cosA}}{\dfrac{sinB}{cosB}}.\dfrac{cos^2B}{sin^2B}\)
\(=\dfrac{sinA}{sinB}.\dfrac{cosB}{cosA}.\dfrac{cos^2B}{sin^2B}\)
\(=\dfrac{a}{b}.\dfrac{\dfrac{a^2+c^2-b^2}{2ac}}{\dfrac{b^2+c^2-a^2}{2bc}}.\dfrac{\left(\dfrac{a^2+c^2-b^2}{2ac}\right)^2}{1-\left(\dfrac{a^2+c^2-b^2}{2ac}\right)^2}\)
\(=\dfrac{a^2+c^2-b^2}{b^2+c^2-a^2}.\dfrac{\left(a^2+c^2-b^2\right)^2}{\left(2ac\right)^2-\left(a^2+c^2-b^2\right)^2}\)
\(=\dfrac{\left(a^2+c^2-b^2\right)^3}{b^2+c^2-a^2}.\dfrac{1}{\left[\left(a+c\right)^2-b^2\right]\left[b^2-\left(a-c\right)^2\right]}\)
\(=\dfrac{\left(a^2+c^2-b^2\right)^3}{b^2+c^2-a^2}.\dfrac{1}{\left(a+b+c\right)\left(a+c-b\right)\left(b+c-a\right)\left(a+b-c\right)}\)
Biến đổi tương tự, ta có BĐT tương đương với BĐT đã cho:
\(\dfrac{\left(a^2+c^2-b^2\right)^3}{b^2+c^2-a^2}+\dfrac{\left(a^2+b^2-c^2\right)^3}{a^2+c^2-b^2}+\dfrac{\left(b^2+c^2-a^2\right)^3}{a^2+b^2-c^2}\ge\left(a+b+c\right)\left(b+c-a\right)\left(a+c-b\right)\left(a+b-c\right)\)
Ta có BĐT phụ sau:
\(\dfrac{x^3}{y}+\dfrac{y^3}{z}+\dfrac{z^3}{x}\ge xy+yz+xz\left(\text{*}\right)\) với \(x,y,z>0\)
Chứng minh:
Áp dụng BĐT cộng mẫu:
\(\dfrac{x^3}{y}+\dfrac{y^3}{z}+\dfrac{z^3}{x}=\dfrac{x^4}{xy}+\dfrac{y^4}{yz}+\dfrac{z^4}{xz}\)
\(\ge\dfrac{\left(x^2+y^2+z^2\right)^2}{xy+yz+xz}\ge\dfrac{\left(xy+yz+xz\right)^2}{xy+yz+xz}=xy+yz+xz\)(đpcm)
Đẳng thức xảy ra khi và chỉ khi \(x=y=z\)
Áp dụng BĐT \(\left(\text{*}\right)\), với đk \(\Delta ABC\) có ba góc nhọn, ta có:
\(\dfrac{\left(a^2+c^2-b^2\right)^3}{b^2+c^2-a^2}+\dfrac{\left(a^2+b^2-c^2\right)^3}{a^2+c^2-b^2}+\dfrac{\left(b^2+c^2-a^2\right)^3}{a^2+b^2-c^2}\ge\left(a^2+c^2-b^2\right)\left(a^2+b^2-c^2\right)+\left(a^2+b^2-c^2\right)\left(b^2+c^2-a^2\right)+\left(b^2+c^2-a^2\right)\left(a^2+c^2-b^2\right)\)
Ta chứng minh được:
\(\left(a^2+c^2-b^2\right)\left(a^2+b^2-c^2\right)+\left(a^2+b^2-c^2\right)\left(b^2+c^2-a^2\right)+\left(b^2+c^2-a^2\right)\left(a^2+c^2-b^2\right)=\left(a+b+c\right)\left(b+c-a\right)\left(a+c-b\right)\left(a+b-c\right)\)
\(=-a^4-b^4-c^4+2a^2b^2+2b^2c^2+2a^2c^2\)
Vậy ta có BĐT cần chứng minh, đẳng thức xảy ra khi và chỉ khi \(\widehat{A}=\widehat{B}=\widehat{C}=60^0\)
Đúng 2
Bình luận (0)