Khi x=0 ta được : \(\sqrt{0}+1\ne2\sqrt{-0}\)

Khi x < 0 thì \(\sqrt{x}\) không xác định .

Khi x > 0 thì \(\sqrt{-x}\) không xác định .

* Vậy trong mọi trường hợp , không có giá trị nào của ẩn nghiệm đúng với phương trình \(\sqrt{x}+1=2\sqrt{-x}\)

\(\sqrt{-x}\) là không thể có trong toán học.

thật tùm bậy

Tập nghiệm của phương trình  x + 1 = 2 - x  là ∅ vì:

Nếu x = 0 thì hai vế có giá trị khác nhau

Nếu x < 0 thì x không xác định vì số âm không có căn bậc hai.

Nếu x > 0 thì  - x  không xác định vì số âm không có căn bậc hai.

\(\sqrt{2-f\left(x\right)}=f\left(x\right)\Leftrightarrow\left\{{}\begin{matrix}f\left(x\right)\ge0\\f^2\left(x\right)+f\left(x\right)-2=0\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}f\left(x\right)=1\\f\left(x\right)=-2< 0\left(loại\right)\end{matrix}\right.\) 

\(\Rightarrow f\left(1\right)=f\left(2\right)=f\left(3\right)=1\)

\(\sqrt{2g\left(x\right)-1}+\sqrt[3]{3g\left(x\right)-2}=2.g\left(x\right)\)

\(VT=1.\sqrt{2g\left(x\right)-1}+1.1\sqrt[3]{3g\left(x\right)-2}\)

\(VT\le\dfrac{1}{2}\left(1+2g\left(x\right)-1\right)+\dfrac{1}{3}\left(1+1+3g\left(x\right)-2\right)\)

\(\Leftrightarrow VT\le2g\left(x\right)\)

Dấu "=" xảy ra khi và chỉ khi \(g\left(x\right)=1\)

\(\Rightarrow g\left(0\right)=g\left(3\right)=g\left(4\right)=g\left(5\right)=1\)

Để các căn thức xác định \(\Rightarrow\left\{{}\begin{matrix}f\left(x\right)-1\ge0\\g\left(x\right)-1\ge0\end{matrix}\right.\)

Ta có:

\(\sqrt{f\left(x\right)-1}+\sqrt{g\left(x\right)-1}+f\left(x\right).g\left(x\right)-f\left(x\right)-g\left(x\right)+1=0\)

\(\Leftrightarrow\sqrt{f\left(x\right)-1}+\sqrt{g\left(x\right)-1}+\left[f\left(x\right)-1\right]\left[g\left(x\right)-1\right]=0\)

\(\Leftrightarrow\left\{{}\begin{matrix}f\left(x\right)=1\\g\left(x\right)=1\end{matrix}\right.\) \(\Leftrightarrow x=3\)

Vậy tập nghiệm của pt đã cho có đúng 1 phần tử

\(ĐK:x\ge1\\ PT\Leftrightarrow\sqrt{x+4}=2-\sqrt{x-1}\\ \Leftrightarrow x+4=x+3-4\sqrt{x-1}\\ \Leftrightarrow4\sqrt{x-1}=-1\Leftrightarrow x\in\varnothing\)

Vậy \(S\in\varnothing\)

TXĐ: \(x>-4\)

Khi đó BPT tương đương:

\(x^2+2x>3\Leftrightarrow x^2+2x-3>0\)

\(\Rightarrow\left[{}\begin{matrix}x>1\\x< -3\end{matrix}\right.\)

Vậy tập nghiệm của BPT là: \(\left[{}\begin{matrix}x>1\\-3< x< -3\end{matrix}\right.\)

S=(1;2]

ĐKXĐ : \(x\ge-2\)

\(\sqrt{x^2-4}-\sqrt{x+2}=0\)

\(\Leftrightarrow\sqrt{x-2}.\sqrt{x+2}-\sqrt{x+2}=0\)

\(\Leftrightarrow\sqrt{x+2}\left(\sqrt{x-2}-1\right)=0\)

\(\Leftrightarrow\left[\begin{array}{nghiempt}\sqrt{x+2}=0\\\sqrt{x-2}-1=0\end{array}\right.\)

\(\Leftrightarrow\left[\begin{array}{nghiempt}x=-2\\x=3\end{array}\right.\) (TMĐK)

Vậy tập nghiệm của pt có 2 phần tử 

\(\sqrt{x^2-4}-\sqrt{x+2}=0\left(ĐK:x\ge-2\right)\)

\(\Leftrightarrow\sqrt{x^2-4}=\sqrt{x+2}\)

\(\Leftrightarrow x^2-4=x+2\)

\(\Leftrightarrow x^2-x-6=0\)

\(\Leftrightarrow x^2+2x-3x-6=0\)

\(\Leftrightarrow x\left(x+2\right)-3\left(x+2\right)=0\)

\(\Leftrightarrow\left(x+2\right)\left(x-3\right)=0\)

\(\Leftrightarrow\left[\begin{array}{nghiempt}x+2=0\\x-3=0\end{array}\right.\)\(\Leftrightarrow\left[\begin{array}{nghiempt}x=-2\\x=3\end{array}\right.\)

có 2 phần tử

x = -2 

x = 3

\(\Leftrightarrow m\left(\sqrt{x^2+2}-1\right)=x\)

\(\Leftrightarrow m=\dfrac{x}{\sqrt{x^2+2}-1}\)

Xét hàm \(f\left(x\right)=\dfrac{x}{\sqrt{x^2+2}-1}\)

\(f'\left(x\right)=\dfrac{2-\sqrt{x^2+2}}{\sqrt{x^2+2}\left(\sqrt{x^2+2}-1\right)^2}\)

\(f'\left(x\right)=0\Rightarrow x=\pm\sqrt{2}\)

\(f\left(\sqrt{2}\right)=\sqrt{2}\) ; \(f\left(-\sqrt{2}\right)=-\sqrt{2}\) ; \(\lim\limits_{x\rightarrow+\infty}f\left(x\right)=1\) ; \(\lim\limits_{x\rightarrow-\infty}f\left(x\right)=-1\)

BBT:

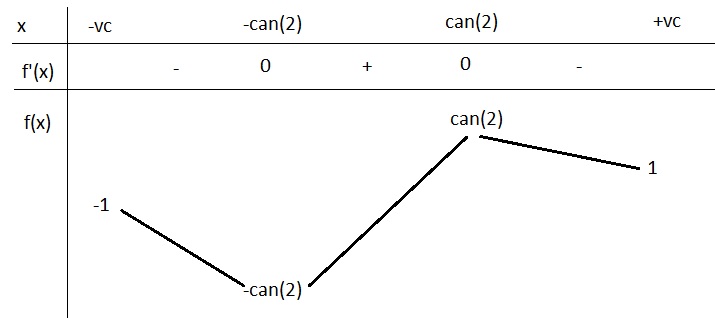
Từ BBT ta thấy pt có 2 nghiệm pb khi \(\left[{}\begin{matrix}-\sqrt{2}< m< -1\\1< m< \sqrt{2}\end{matrix}\right.\)

\(a,ĐK:x\ge\dfrac{1}{5}\\ PT\Leftrightarrow5x-1=64\\ \Leftrightarrow x=13\left(tm\right)\\ b,ĐK:x\ge\dfrac{2}{5}\\ BPT\Leftrightarrow5x-2< 16\\ \Leftrightarrow x< \dfrac{18}{5}\\ \Leftrightarrow\dfrac{2}{5}\le x< \dfrac{18}{5}\\ c,ĐK:x\ge3\\ PT\Leftrightarrow\left|x-1\right|-\left|x-2\right|=x-3\\ \Leftrightarrow\left[{}\begin{matrix}1-x-\left(2-x\right)=x-3\left(x< 1\right)\\x-1-\left(2-x\right)=x-3\left(1\le x< 2\right)\\x-1-\left(x-2\right)=x-3\left(x\ge2\right)\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}x=2\left(ktm\right)\\x=0\left(tm\right)\\x=4\left(tm\right)\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=4\end{matrix}\right.\)