Question

Tìm tập các giá trị của m sao cho phương trình \(m\sqrt{x^2+2}=x+m\) có 2 nghiệm phân biệt.

Answer 1

\(\Leftrightarrow m\left(\sqrt{x^2+2}-1\right)=x\)

\(\Leftrightarrow m=\dfrac{x}{\sqrt{x^2+2}-1}\)

Xét hàm \(f\left(x\right)=\dfrac{x}{\sqrt{x^2+2}-1}\)

\(f'\left(x\right)=\dfrac{2-\sqrt{x^2+2}}{\sqrt{x^2+2}\left(\sqrt{x^2+2}-1\right)^2}\)

\(f'\left(x\right)=0\Rightarrow x=\pm\sqrt{2}\)

\(f\left(\sqrt{2}\right)=\sqrt{2}\) ; \(f\left(-\sqrt{2}\right)=-\sqrt{2}\) ; \(\lim\limits_{x\rightarrow+\infty}f\left(x\right)=1\) ; \(\lim\limits_{x\rightarrow-\infty}f\left(x\right)=-1\)

BBT:

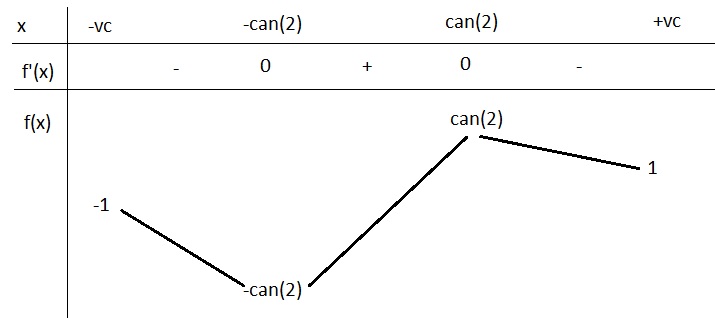
Từ BBT ta thấy pt có 2 nghiệm pb khi \(\left[{}\begin{matrix}-\sqrt{2}< m< -1\\1< m< \sqrt{2}\end{matrix}\right.\)