Cho tỉ lệ thức a/b=c/d.Cmr:
a,21a+34b/21a-34b= 21c+34d/21c-34d
b,a^2+b^2/c^2+d^2 = ab/cd
Cho \(a,b,c>0\) thỏa mãn \(a+b+c=62\)
Tìm GTLN của \(P=\sqrt{5a^2+38ab+21b^2}+\sqrt{5b^2+38bc+21c^2}+\sqrt{5c^2+38ca+21a^2}\)
men đợi t chút nha hơi dài á
\(\sqrt{5a^2+38ab+21b^2}=\sqrt{5a^2+8ab+30ab+21b^2}\le\sqrt{9a^2+30ab+25b^2}=3a+5b\)
Làm nốt :D
Ta có: \(P=\sqrt{5a^2+38ab+21b^2}+\sqrt{5b^2+38bc+21c^2}+\sqrt{5c^2+38ca+21a^2}\)
\(=\sqrt{\left(a+7b\right)\left(5a+3b\right)}+\sqrt{\left(b+7c\right)\left(5b+3c\right)}+\sqrt{\left(c+7a\right)\left(5c+3a\right)}\)
Áp dụng BĐT côsi cho 3 số dương a,b,c ta có:
\(\sqrt{\left(a+7b\right)\left(5a+3b\right).\frac{246016}{9}}\le\frac{a+7b+5a+3b+\frac{240616}{9}}{2}\left(1\right)\)
\(\sqrt{\left(b+7c\right)\left(5b+3c\right).\frac{246016}{9}}\le\frac{b+7c+5b+3c+\frac{246016}{9}}{2}\left(2\right)\)
\(\sqrt{\left(c+7a\right)\left(5c+3a\right).\frac{246016}{9}}\le\frac{c+7a+5c+3a+\frac{246016}{9}}{2}\left(3\right)\)
Lấy \(\left(1\right)+\left(2\right)+\left(3\right)\)ta được:
\(P+\frac{496}{3}\le\frac{16\left(a+b+c\right)+\frac{246016}{9}}{2}\)
\(\Leftrightarrow P+\frac{496}{3}\le\frac{16.62+\frac{246016}{9}}{2}\)
\(\Leftrightarrow P+\frac{496}{3}\le\frac{127472}{9}\)
\(\Leftrightarrow P\le\frac{125984}{9}\)
Dấu"="xảy ra \(\Leftrightarrow a+b+c=\frac{62}{3}\)
Vậy \(P_{max}=\frac{125984}{9}\)\(\Leftrightarrow a+b+c=\frac{62}{3}\)
TÌM X:
A) [124-(20-4x)]:20=12
B)1 phần 3 :(2x-1)= -4 phần 21
C) (1 phần 2.3 + 1 phần 3.4+...+1 phần 8.9 + 1 phần 9.1).x= 1 phần 5
giúp em với ạ biết đáp án là
A)34
B)-3 phần 8
C) 1 phần 2
cần tìm bước giải
A) [124 - (20 - 4x)] = 12 . 20
[124 - (20 - 4x)] = 240
(20 - 4x) = 240 - 124
(20 - 4x) = 116
4x = 116 + 20
4x = 136
x = 136 : 4
x = 34
B) (2x - 1) = 1/3 : -4/21
2x - 1 = -7/4
2x = -7/4 + 1
2x = -3/4
x = -3/4 : 2
x = -3/8
giải giúp mình 16.3 , 21a, 21b , 21c vở bt vật lí 6
(bn tham khảo: http://vietjack.com/giai-sach-bai-tap-vat-li-6/bai-16-rong-roc.jsp)

(21a b c j đó bn vào link kia xem)
cho tỉ lệ thức a/b = c/d. chứng minh các tỉ lệ thức sau a^2-b^2 / ab = c^2-d^2/cd ,
Lần sau bạn cho thêm cả dấu ngoặc cho dễ hiểu nhé :v
Đặt \(\frac{a}{b}=\frac{c}{d}=k\) => \(\left\{{}\begin{matrix}a=b.k\\c=d.k\end{matrix}\right.\) \(\left(b,d\ne0\right)\)
Thay \(\left\{{}\begin{matrix}a=b.k\\c=d.k\end{matrix}\right.\) vào \(\frac{a^2-b^2}{ab}\) và \(\frac{c^2-d^2}{cd}\) ta có :
\(\left\{{}\begin{matrix}\frac{\left(b.k\right)^2-b^2}{b.k.b}\\\frac{\left(d.k\right)^2-d^2}{d.k.d}\end{matrix}\right.\) <=> \(\left\{{}\begin{matrix}\frac{b^2.k^2-b^2}{b^2.k}\\\frac{d^2.k^2-d^2}{d^2.k}\end{matrix}\right.\) <=> \(\left\{{}\begin{matrix}\frac{b^2\left(k^2-1\right)}{b^2.k}\\\frac{d^2\left(k^2-1\right)}{d^2.k}\end{matrix}\right.\) <=>\(\left\{{}\begin{matrix}\frac{k^2-1}{k}\\\frac{k^2-1}{k}\end{matrix}\right.\)(vì b,d khác 0 nên \(b^2,d^2\) khác 0)
=> \(\frac{a^2-b^2}{ab}\) = \(\frac{c^2-d^2}{cd}\) (vì cùng bằng \(\frac{k^2-1}{k}\))
vậy \(\frac{a^2-b^2}{ab}\) = \(\frac{c^2-d^2}{cd}\) nếu \(\frac{a}{b}=\frac{c}{d}\)
lâu lắm không làm nên không chắc đâu :v
Trong các miếng bìa ở hình 21a, 21b, 21c, 21d, miếng bìa nào có thể gấp (theo các nét đứt) và dán lại để được hình chóp tam giác đều? Hình chóp tứ giác đều?
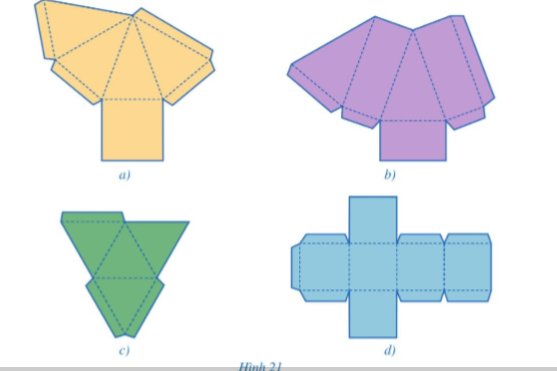
Hình a là hình chóp tam giác đều
Hình c là hình chóp tứ giác đều
Cho tỉ lệ thức \(\dfrac{a}{b}=\dfrac{c}{d}\) . Chứng minh rằng ta có các tỉ lệ thức sau (giả thiết các tỉ lệ thức là có nghĩa ) :
a) \(\dfrac{ab}{cd}=\dfrac{a^2-b^2}{c^2-d^2}\)
b) \(\left(\dfrac{a+b}{c+d}\right)^2=\dfrac{a^2+b^2}{c^2+d^2}\)
cho tỉ lệ thức a/b=c/d hãy suy ra tỉ lệ thức ab/cd=a^2-b^2/c^2-d^2
2 tick câu này nhé
\(\frac{a}{b}=\frac{c}{d}\Rightarrow\frac{a}{c}=\frac{b}{d}\Rightarrow\frac{a^2}{c^2}=\frac{b^2}{d^2}=\frac{a^2-b^2}{c^2-d^2}\)mà\(\frac{a^2}{c^2}=\frac{a}{c}.\frac{a}{c}=\frac{a}{c}.\frac{b}{d}=\frac{ab}{cd}\Rightarrow\frac{ab}{cd}=\frac{a^2-b^2}{c^2-d^2}\)
Cho tỉ lệ thức: a/b=c/d. Chứng minh
a) ab/cd = a^2 - b^2/ c^2-d^2
b) ab/cd = (a-b)^2/ (c-d)^2
a)Vì \(\frac{a}{b}=\frac{c}{d}\Rightarrow\frac{a}{c}=\frac{b}{d}\)
\(\Rightarrow\frac{a^2}{c^2}=\frac{b^2}{d^2}\)
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
\(\frac{a^2}{c^2}=\frac{b^2}{d^2}=\frac{a^2-b^2}{c^2-d^2}\)
\(\frac{a}{b}=\frac{c}{d}\) => \(\frac{a}{c}=\frac{b}{d}\)
=> \(\frac{a^2}{c^2}=\frac{b^2}{d^2}=\frac{ab}{cd}\)
Áp dụng dãy tỉ số bằng nhau ta có;
\(\frac{a^2}{c^2}=\frac{b^2}{d^2}=\frac{ab}{cd}=\frac{a^2-b^2}{c^2-d^2}\)
=> đpcm
Chúc bạn làm bài tốt
b) Vì \(\frac{a}{b}=\frac{c}{d}\Rightarrow\frac{a}{c}=\frac{b}{d}=\left(\frac{a}{c}\right)^2=\left(\frac{b}{d}\right)^2\)
Áp dụng tính chất dãy tỉ số bằng nhau :
\(\frac{a}{c}=\frac{b}{d}=\left(\frac{a}{c}\right)^2=\left(\frac{b}{d}\right)^2=\frac{\left(a-b\right)^2}{\left(c-d\right)^2}\) (đpcm)
cho tỉ lệ thức a/b=c/d .CMR: a/b=c/d cmr ab/cd=a^2-b^2/ab=c^2-d^2/cd và (a+b)^2/a^2+b^2=(c+d)^2/c^2+d^2