Hướng dẫn mình bài này với ạ!
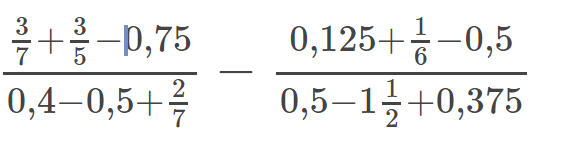
Giúp mình mấy câu này với, nếu được thì có thể hướng dẫn mình làm bài này với được không ạ
like playing soccer, don't you
goes to school late, doesn't he
can swim very well, can't you
is going to the party, isn't she
was published in Germany in 1550, wasn't it
are sold all over the world, aren't they
have been built this year, haven't they
was given a book, wasn't he
were bought by Mrs Brown yesterday, weren't they
is used everyday, isn't it
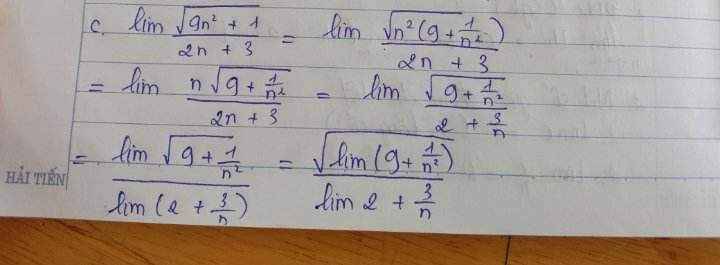 Bài này cô mình giải mà mình không hiểu cách làm ai hướng dẫn mình với ạ
Bài này cô mình giải mà mình không hiểu cách làm ai hướng dẫn mình với ạ
hướng dẫn mình bài này ạ mình cần gấp rút cực kỳ các bạn giúp mình với
18725 chia 206
3160 chia 56
41982 chia 206 với ạ
18725:206=90 dư 185
3160:56=56 dư 3
41982:206=203 dư 82
hướng dẫn mình chi tiết bài này được không ạ?
Giúp em giải hoặc hướng dẫn em làm bài này với ạ
\(=\dfrac{1}{120}-\dfrac{2}{3}\left(\dfrac{1}{30}-\dfrac{1}{33}+\dfrac{1}{33}-\dfrac{1}{36}+...+\dfrac{1}{117}-\dfrac{1}{120}\right)\)
\(=\dfrac{1}{120}-\dfrac{2}{3}\left(\dfrac{1}{30}-\dfrac{1}{120}\right)\)
\(=-\dfrac{1}{120}\)
\(\sqrt{50-\sqrt{18}}\)( hướng dẫn giúp mình bt này với ạ)
\(\sqrt{48}-\sqrt{3} \) ( hướng dẫn giúp mình bt này với ạ)
`\sqrt{48}-\sqrt{3}=\sqrt{4^2 . 3}-\sqrt{3}=4\sqrt{3}-\sqrt{3}=3\sqrt{3}`
Tìm x:
A) 7,2_0,25+x=10
B)20_4,5_x=12,75
Hướng dẫn giải giúp e bài này với ạ.
A) 7,2 - 0,25 + x = 10
6,95 + x = 10
x = 10 - 6,95
x = 3,05
B) 20 - 4,5 - x = 12,75
15,5 - x = 12,75
x = 15,5 - 12,75
x = 2,75
Thầy cô hướng dẫn giúp e bài này ạ, e cảm ơn ạ
Gọi D là trung điểm AC
Trong mp (ABC), qua A kẻ đường thẳng vuông góc AB, qua C kẻ đường thẳng vuông góc AC, chúng cắt nhau tại H
Dễ dàng nhận ra hai tam giác vuông HAC và HAB có cặp cạnh huyền - cạnh góc vuông bằng nhau nên 2 tam giác bằng nhau
\(\Rightarrow HA=HC\Rightarrow H\) nằm trên trung trực AC (do AB=BC)
\(\Rightarrow H,A,D\) thẳng hàng
\(\left\{{}\begin{matrix}CH\perp BC\\SC\perp BC\left(gt\right)\end{matrix}\right.\) \(\Rightarrow BC\perp\left(SHC\right)\Rightarrow BC\perp SH\)
Tương tự ta có \(AB\perp\left(SHA\right)\Rightarrow AB\perp SH\)
\(\Rightarrow SH\perp\left(ABC\right)\)
Gọi E là trung điểm AH \(\Rightarrow ME\) là đường trung bình tam giác SAH
\(\Rightarrow ME||SH\Rightarrow ME\perp\left(ABC\right)\) đồng thời \(ME=\dfrac{1}{2}SH\)
Gọi G là trung điểm BC \(\Rightarrow AG\perp BC\), từ D kẻ \(DF\perp BC\Rightarrow DF||AG\Rightarrow DF\) là đường trung bình tam giác AGC
\(\Rightarrow DF=\dfrac{1}{2}AG=\dfrac{a\sqrt{3}}{4}\)
AGCH là hình thang (AG song song CH vì cùng vuông góc BC) \(\Rightarrow EF\) là đường trung bình hình thang
\(\Rightarrow EF\perp BC\Rightarrow E,D,F\) thẳng hàng
\(AH=\dfrac{AD}{cos\widehat{DAH}}=\dfrac{AD}{cos\widehat{ABD}}=\dfrac{AD}{cos30^0}=\dfrac{a\sqrt{3}}{3}\)
\(ED=\dfrac{1}{2}AH=\dfrac{a\sqrt{3}}{6}\) (trung tuyến tam giác vuông)
\(\Rightarrow EF=ED+DF=\dfrac{5a\sqrt{3}}{12}\)
Trong tam giác vuông MEF, từ E kẻ \(EK\perp MF\)
\(\left\{{}\begin{matrix}ME\perp\left(ABC\right)\Rightarrow ME\perp BC\\EF\perp BC\end{matrix}\right.\) \(\Rightarrow BC\perp\left(MEF\right)\Rightarrow BC\perp EK\)
\(\Rightarrow EK\perp\left(MBC\right)\Rightarrow EK=d\left(E;\left(MBC\right)\right)\)
\(SB=2NB\Rightarrow d\left(S;\left(MBC\right)\right)=2d\left(N;\left(MBC\right)\right)\)
\(SM=AM\Rightarrow d\left(S;\left(MBC\right)\right)=d\left(A;\left(MBC\right)\right)\)
\(AC=2DC\Rightarrow d\left(A;\left(MBC\right)\right)=2d\left(D;\left(MBC\right)\right)\)
\(\dfrac{EF}{DF}=\dfrac{5}{3}\Rightarrow d\left(E;\left(MBC\right)\right)=\dfrac{5}{3}d\left(D;\left(MBC\right)\right)=\dfrac{5}{3}d\left(N;\left(MBC\right)\right)\)
\(\Rightarrow EK=\dfrac{5}{3}.\dfrac{3a}{7}=\dfrac{5a}{7}\)
\(\dfrac{1}{EK^2}=\dfrac{1}{ME^2}+\dfrac{1}{EF^2}\Rightarrow ME=\dfrac{EF.EK}{\sqrt{EF^2-EK^2}}=5a\)
\(\Rightarrow SH=2ME=10a\)
\(V=\dfrac{1}{3}.10a.\dfrac{a^2\sqrt{3}}{4}=\dfrac{5a^3\sqrt{3}}{6}\)