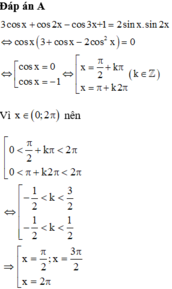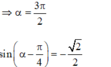biết cosx=4/5. Tính B= cos^4x.sin²x + cos²x.sin^4x

Những câu hỏi liên quan
Cho 00 x 900. Chứng minh các đẳng thức sau:
1. sin6 x +cos6 x 1 - 3sin2 x cos2 x.
2. sin4 x - cos4 x 1 - 2cos2 x.
3. tan2 x - sin2 x tan2 x.sin2x.
4. cot2 x - cos2 x cot2 x.cos2 x.
5.left(sqrt{dfrac{1+sinx}{1-sinx}}-sqrt{dfrac{1-sinx}{1+sinx}}right)^2 4 tan2 x.
6.left(sqrt{dfrac{1+cosx}{1-cosx}}-sqrt{dfrac{1-cosx}{1+cosx}}right)^2 4 cot2 x.
Đọc tiếp
Cho 00 < x < 900. Chứng minh các đẳng thức sau:
1. sin6 x +cos6 x = 1 - 3sin2 x cos2 x.
2. sin4 x - cos4 x = 1 - 2cos2 x.
3. tan2 x - sin2 x = tan2 x.sin2x.
4. cot2 x - cos2 x = cot2 x.cos2 x.
5.\(\left(\sqrt{\dfrac{1+sinx}{1-sinx}}-\sqrt{\dfrac{1-sinx}{1+sinx}}\right)^2\) = 4 tan2 x.
6.\(\left(\sqrt{\dfrac{1+cosx}{1-cosx}}-\sqrt{\dfrac{1-cosx}{1+cosx}}\right)^2\) = 4 cot2 x.
1: \(sin^6x+cos^6x+3sin^2x\cdot cos^2x\)
\(=\left(sin^2x+cos^2x\right)^2-3\cdot sin^2x\cdot cos^2x\cdot\left(sin^2x+cos^2x\right)+3\cdot sin^2x\cdot cos^2x\)
=1
2: \(sin^4x-cos^4x\)
\(=\left(sin^2x+cos^2x\right)\left(sin^2x-cos^2x\right)\)
\(=1-2\cdot cos^2x\)
Đúng 0
Bình luận (0)
cos 4x + tan x.sin 4x = 1
ĐKXĐ: ...
\(\Leftrightarrow cos4x+\frac{sinx}{cosx}.4sinx.cosx.cos2x=1\)
\(\Leftrightarrow2cos^22x-1+4sin^2x.cos2x=1\)
\(\Leftrightarrow cos^22x+\left(1-cos2x\right)cos2x=1\)
\(\Leftrightarrow cos2x=1\Rightarrow x=k\pi\)
Đúng 0
Bình luận (0)
Rút gọn:
a. \(S=1-sin^2x+sin^4x-sin^6x+...+\left(-1\right)^nsin^{2n}x+...\) với sinx \(\ne\pm1\)
b. \(S=1+cos^2x+cos^4x+cos^6x+...+cos^{2n}x+...\) với cosx \(\ne\pm1\)
c. \(S=1-tanx+tan^2x-tan^3x+...\) với \(0< x< \dfrac{\pi}{4}\)
a.
Tổng là cấp số nhân lùi vô hạn với \(\left\{{}\begin{matrix}u_1=1\\q=-sin^2x\end{matrix}\right.\)
Do đó: \(S=\dfrac{u_1}{1-q}=\dfrac{1}{1+sin^2x}\)
b. Tương tự, tổng cấp số nhân lùi vô hạn với \(\left\{{}\begin{matrix}u_1=1\\q=cos^2x\end{matrix}\right.\)
\(\Rightarrow S=\dfrac{1}{1-cos^2x}=\dfrac{1}{sin^2x}\)
c. Do \(0< x< \dfrac{\pi}{4}\Rightarrow0< tanx< 1\)
Tổng trên vẫn là tổng cấp số nhân lùi vô hạn với \(\left\{{}\begin{matrix}u_1=1\\q=-tanx\end{matrix}\right.\)
\(\Rightarrow S=\dfrac{1}{1+tanx}\)
Đúng 1
Bình luận (0)
Gọi α là nghiệm lớn nhất của phương trình 3.cos x + cos 2x – cos 3x + 1 2.sin x.sin 2x thuộc khoảng
0
,
2
π
. Tính
sin
α
-
π
4
.
A
.
-
2...
Đọc tiếp
Gọi α là nghiệm lớn nhất của phương trình 3.cos x + cos 2x – cos 3x + 1 = 2.sin x.sin 2x thuộc khoảng 0 , 2 π . Tính sin α - π 4 .
A . - 2 2
B . 2 2
C . 0
D . 1
chứng minh rằng
a) tanx(cot\(^2\)x - 1) = cotx(1 - tan\(^2\)x)
b) tan\(^2\)x - sin\(^2\)x = tan\(^2\)x.sin\(^2\)x
c) \(\dfrac{cos^2x-sin^2x}{cot^2x-tan^2x}\) - cos\(^2\)x = - cos\(^4\)x
a: tan x(cot^2x-1)
\(=\dfrac{1}{cotx}\left(cot^2x-cotx\cdot tanx\right)\)
=cotx-tanx/cotx=cotx(1-tan^2x)
b: \(tan^2x-sin^2x=\dfrac{sin^2x}{cos^2x}-sin^2x\)
\(=sin^2x\left(\dfrac{1}{cos^2x}-1\right)=sin^2x\cdot\dfrac{sin^2x}{cos^2x}=sin^2x\cdot tan^2x\)
c: \(\dfrac{cos^2x-sin^2x}{cot^2x-tan^2x}=\dfrac{cos^2x-sin^2x}{\dfrac{cos^2x}{sin^2x}-\dfrac{sin^2x}{cos^2x}}\)
\(=\left(cos^2x-sin^2x\right):\dfrac{cos^4x-sin^4x}{sin^2x\cdot cos^2x}\)
\(=\dfrac{sin^2x\cdot cos^2x}{1}=sin^2x\cdot cos^2x\)
=>sin^2x*cos^2x-cos^2x=cos^2x(sin^2x-1)
=-cos^2x*cos^2x=-cos^4x
=>ĐPCM
Đúng 1
Bình luận (0)
Giải pt :
cos2x.sin4x + cos2x = 2cosx (sin x + cos x) -1
Giúp mình với mn...
1)cos2x+cos22x+cos23x+cos24x=2
2) (1-tanx) (1+sin2x)=1+tanx
3) tan2x=sin3x.cosx
4) tanx +cot2x=2cot4x
5) sinx+sin2x+sin3x=cosx+cos2x+cos3x
6)sinx=√2 sin5x-cosx
7) 1/sin2x + 1/cos2x =2/sin4x
8) sinx+cosx=cos2x/1-sin2x
9)1+cos2x/cosx= sin2x/1-cos2x
10)sin3x+cos3x/2cosx-sinx=cos2x
1. Tìm tập xác định của hàm số
y = sin√1+x/1-x ( căn toàn bộ biểu thức)
2. Tìm tập xác định của HS
c) y = 2 / cosx - cos3x ( cosx và cos3x đều ở dưới mẫu)
3. Tìm GTLN và GTNN
a) y = 3 - 2|sinx|
b) y = cosx + cos(x - π/3)
c) y = cos^2x +2cos2x
d) y = ✓5 - 2cos^x.sin^2x ( căn toàn bộ biểu thức)
1.
ĐKXĐ: \(\frac{1+x}{1-x}\ge0\Leftrightarrow-1\le x< 1\)
2.
\(cosx-cos3x\ne0\)
\(\Leftrightarrow cos3x\ne cosx\)
\(\Leftrightarrow\left\{{}\begin{matrix}3x\ne x+k2\pi\\3x\ne-x+k2\pi\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x\ne k\pi\\x\ne\frac{k\pi}{2}\end{matrix}\right.\) \(\Leftrightarrow x\ne\frac{k\pi}{2}\)
3.
a. \(0\le\left|sinx\right|\le1\Rightarrow1\le y\le3\)
\(y_{min}=1\) khi \(\left|sinx\right|=1\)
\(y_{max}=3\) khi \(sinx=0\)
b. \(y=cosx+cos\left(x-\frac{\pi}{3}\right)=2cos\left(x-\frac{\pi}{6}\right).cos\frac{\pi}{6}=\sqrt{3}cos\left(x-\frac{\pi}{6}\right)\)
\(-1\le cos\left(x-\frac{\pi}{6}\right)\le1\Rightarrow-\sqrt{3}\le y\le\sqrt{3}\)
c. \(y=cos^22x+2cos2x+1-1=\left(cos2x+1\right)^2-1\ge-1\)
\(y_{min}=-1\) khi \(cos2x=-1\)
\(cos2x\le1\Leftrightarrow\left\{{}\begin{matrix}cos^22x\le1\\2cos2x\le2\end{matrix}\right.\) \(\Rightarrow y\le3\)
\(y_{max}=3\) khi \(cos2x=1\)
d. \(5-2cos^2x.sin^2x=5-\frac{1}{2}\left(2sinx.cosx\right)^2=5-\frac{1}{2}sin^22x\)
\(0\le sin^22x\le1\Rightarrow\frac{9}{2}\le5-\frac{1}{2}sin^22x\le5\)
\(\Rightarrow\sqrt{\frac{9}{2}}\le y\le\sqrt{5}\)
Đúng 0
Bình luận (0)
chứng minh rằng : sin\(^4\)x+cos\(^4\)x=1 - 2cos\(^2\)x.sin\(^2\)x
\(sin^4\left(x\right)+cos^4\left(x\right)+2sin^2\left(x\right)cos^2\left(x\right)=\left[sin^2\left(x\right)+cos^2\left(x\right)\right]^2=1^2=1\\ \Rightarrow sin^4\left(x\right)+cos^4\left(x\right)=1-2sin^2\left(x\right)cos^2\left(x\right)\left(đpcm\right)\)
Đúng 0
Bình luận (0)
sin^4x+cos^4x
=(sin^2x+cos^2x)^2-2*sin^2x*cos^2x
=1-2*cos^2x*sin^2x
Đúng 0
Bình luận (0)