Ta có: \(x^2+y^2+z^2=1\)

\(\Rightarrow x\le1,y\le1,z\le1\)

\(\Rightarrow x-1\le0,y-1\le0,z-1\le0\)

\(\Rightarrow x^2\left(x-1\right)\le0,y^2\left(y-1\right)\le0,z^2\left(z-1\right)\le0\) 

(vì \(x^2,y^2,z^2\ge0\))

\(\Rightarrow x^2\left(x-1\right)+y^2\left(y-1\right)+z^2\left(z-1\right)\le0\).

hay \(x^3+y^3+z^3\le x^2+y^2+z^2=1\).

Dấu "=" xảy ra khi \(\left\{{}\begin{matrix}x^2\left(x-1\right)=0\\y^2\left(y-1\right)=0\\z^2\left(z-1\right)=0\end{matrix}\right.\) và \(x^2+y^2+z^2=1\)

\(\Leftrightarrow\left(x,y,z\right)=\left(0;0;1\right)\) và các hoán vị.

Mặt khác theo giả thiết: \(x^3+y^3+z^3=1\).

\(\Rightarrow\left(x,y,z\right)=\left(0;0;1\right)\) và các hoán vị.

\(\Rightarrow xyz=0\)

Sửa đề: \(P=x^{2008}+y^{2009}+z^{2010}\)

Ta có: x+y+z=1

nên \(\left(x+y+z\right)^3=1\)

\(\Leftrightarrow x^3+y^3+z^3+3\left(x+y\right)\left(y+z\right)\left(x+z\right)=1\)

\(\Leftrightarrow3\left(x+y\right)\left(y+z\right)\left(z+x\right)+1=1\)

\(\Leftrightarrow3\left(x+y\right)\left(y+z\right)\left(x+z\right)=0\)

mà 3>0

nên \(\left(x+y\right)\left(y+z\right)\left(x+z\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x+y=0\\y+z=0\\x+z=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-y\\y=-z\\x=-z\end{matrix}\right.\)

Thay x=-y vào biểu thức \(x+y+z=1\), ta được:

\(-y+y+z=1\)

hay z=1

Thay x=-y và z=1 vào biểu thức \(x^2+y^2+z^2=1\), ta được:

\(\left(-y\right)^2+y^2+1=1\)

\(\Leftrightarrow y^2+y^2=0\)

\(\Leftrightarrow2y^2=0\)

hay y=0

Vì x=-y

và y=0

nên x=0

Thay x=0; y=0 và z=1 vào biểu thức \(P=x^{2008}+y^{2009}+z^{2010}\), ta được:

\(P=0^{2008}+0^{2009}+1^{2010}=1\)

Vậy: P=1

Đáp án B

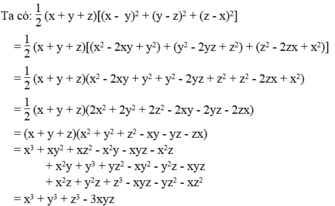
Vế trái bằng vế phải nên đẳng thức được chứng minh.

Nếu x ≥ 0, y  ≥  0, z  ≥  0 thì:

x + y + z  ≥  0

x - y 2 + y - z 2 + z - x 2 ≥ 0

Suy ra:

x 3 + y 3 + z 3 - 3 x y z ≥ 0 ⇔ x 3 + y 3 + z 3 ≥ 3 x y z

Hay:  x 3 + y 3 + z 3 3 ≥ x y z

Ta có: \(x^3-y^3=3x-3y\Leftrightarrow x^2+xy+y^2=3\) (Do \(x\neq y\)).

Tương tự: \(y^2+yz+z^2=3;z^2+zx+x^2=3\).

Cộng vế với vế ta có: \(2\left(x^2+y^2+z^2\right)+xy+yz+zx=9\)

\(\Leftrightarrow\dfrac{3\left(x^2+y^2+z^2\right)}{2}+\dfrac{\left(x+y+z\right)^2}{2}=9\).

Mặt khác, từ đó ta cũng có: \(\left(x^2+xy+y^2\right)-\left(y^2+yz+z^2\right)=0\Leftrightarrow\left(x+y+z\right)\left(x-z\right)=0\Leftrightarrow x+y+z=0\).

Do đó \(x^2+y^2+z^2=6\left(đpcm\right)\).

Cặc

Biến đổi tương đương nhé bạn.

a: Ta có: \(\left(x+y\right)^2\)

\(=x^2+2xy+y^2\)

\(\Leftrightarrow x^2+y^2=\dfrac{\left(x+y\right)^2}{2xy}\ge\dfrac{\left(x+y\right)^2}{2}\forall x,y>0\)