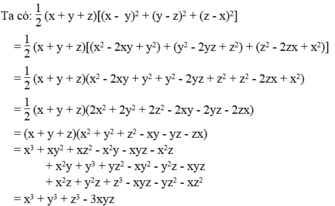
Vế trái bằng vế phải nên đẳng thức được chứng minh.
Nếu x ≥ 0, y ≥ 0, z ≥ 0 thì:
x + y + z ≥ 0
x - y 2 + y - z 2 + z - x 2 ≥ 0
Suy ra:
x 3 + y 3 + z 3 - 3 x y z ≥ 0 ⇔ x 3 + y 3 + z 3 ≥ 3 x y z
Hay: x 3 + y 3 + z 3 3 ≥ x y z
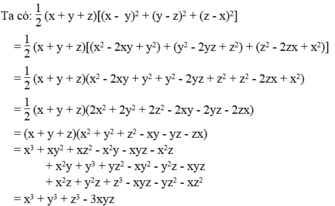
Vế trái bằng vế phải nên đẳng thức được chứng minh.
Nếu x ≥ 0, y ≥ 0, z ≥ 0 thì:
x + y + z ≥ 0
x - y 2 + y - z 2 + z - x 2 ≥ 0
Suy ra:
x 3 + y 3 + z 3 - 3 x y z ≥ 0 ⇔ x 3 + y 3 + z 3 ≥ 3 x y z
Hay: x 3 + y 3 + z 3 3 ≥ x y z
Chứng minh
x^3+y^3+z^3-3xyz=1/2(x+y+z)[(x-y)^2+(y-z)^2+(z-x)^2]
cho 3 số dương x,y,z thỏa mãn x+y+z=3.
chứng minh: \(\dfrac{x}{1+y^2}+\dfrac{y}{1+z^2}+\dfrac{z}{1+x^2}\ge\dfrac{3}{2}\)
Cho các số dương x,y,z và \(x^2+y^2+z^2=1\).Chứng minh rằng:\(\dfrac{x^3}{y+2z}+\dfrac{y^3}{z+2x}+\dfrac{z^3}{x+2y}\ge\dfrac{1}{3}\)
cho x;y;z>=0 và x+y+z>=1.hãy chứng minh x^3/y^2+y^3/z^2+z^3/x^2
giup minh nhanh nha
cho x,y,z > 0 và x^2 + y^2 + z^2 = 1
chứng minh : \(\frac{1}{x^2+y^2}+\frac{1}{y^2+z^2}+\frac{1}{z^2+x^2}>3\frac{x^3+y^3+z^3}{2xyz}\)
a, Cho x, y, z > 0 \(\in[0,1]\). Chứng minh:
\(\dfrac{x}{yz+1}+\dfrac{y}{xz+1}+\dfrac{z}{xy+1}< 2\)
b, x, y, z > 0 : xyz = 1. Chứng minh:
\(\dfrac{1}{x^2+2y+3}+\dfrac{1}{y^2+2z^2+3}+\dfrac{1}{z^2+2x^2+3}\le2\)
Cho 3 số x,y,z thỏa mãn x+y+z=3
Chứng minh: \(\frac{x}{1+y^2}+\frac{y}{1+z^2}+\frac{z}{1+x^2}>=\frac{3}{2}\)
Cho x , y , z > 0
Chứng minh rằng
\(\frac{2\sqrt{x}}{x^3+y^2}+\frac{2\sqrt{y}}{y^3+z^2}+\frac{2\sqrt{z}}{z^3+x^2}\le\frac{1}{x^2}+\frac{1}{y^2}+\frac{1}{z^2}\)
Chứng minh: \(x^3+y^3+z^3-3xyz=\frac{1}{2}\left(x+y+z\right)\orbr{ }\left(x-y\right)^2+\left(y-z\right)^2+\left(z-x\right)^2\)}
chứng minh rằng \(\frac{x^3}{z+x^2}+\frac{y^3}{x+y^2}+\frac{z^3}{y+z^2}\ge\frac{1}{2}\left(\frac{1}{x}+\frac{1}{y}+\frac{1}{z}\right)\)