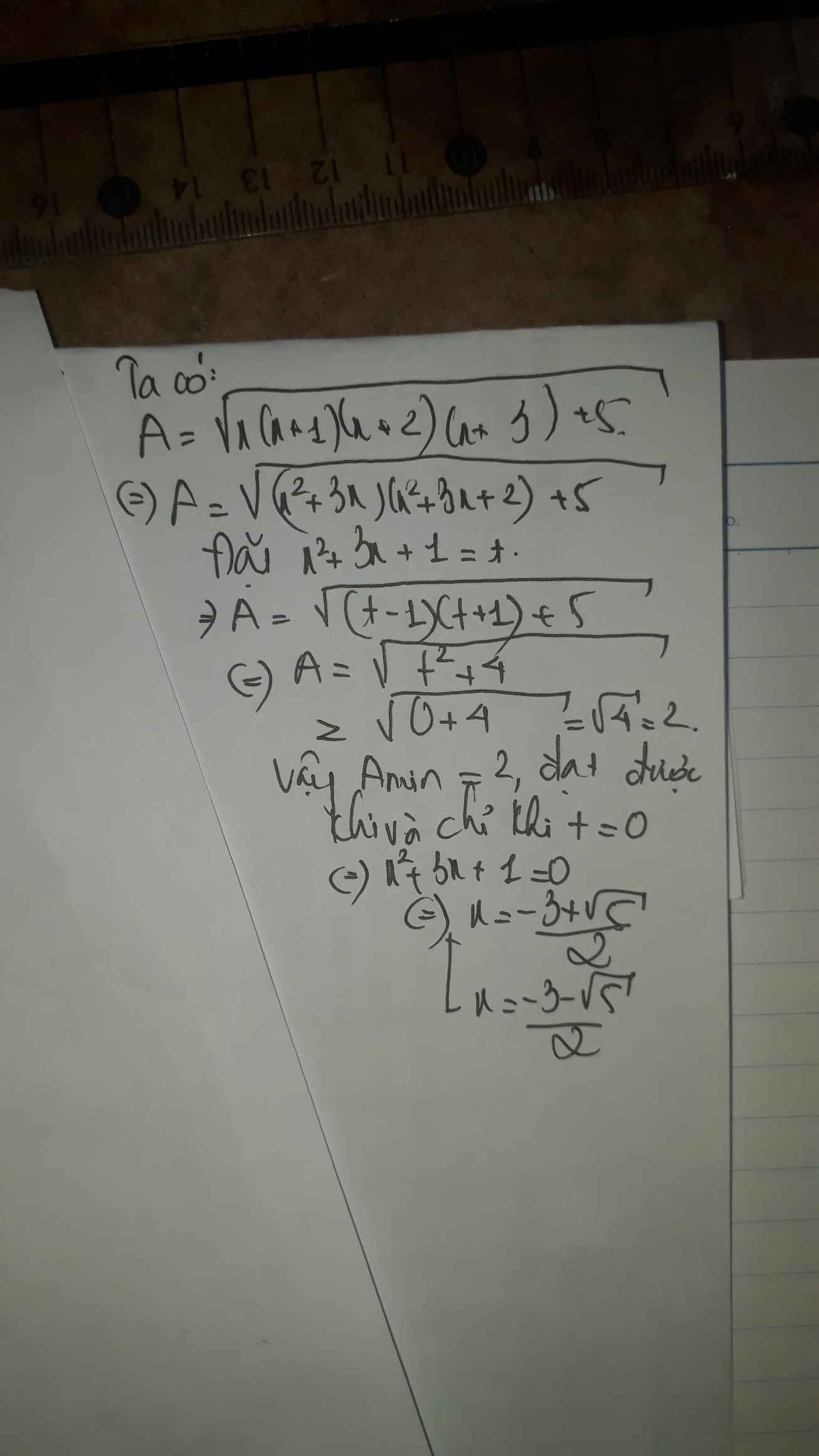Tìm GTNN của \(\left(x^2+2\right)^2\)

Những câu hỏi liên quan
1. Tìm GTNN của \(y=x+\dfrac{1}{x}-5\) trên \(\left(0,+\infty\right)\)
2. Tìm GTNN của \(y=4x^2+\dfrac{1}{x}-4\) trên \(\left(0,+\infty\right)\)
3. Tìm GTLN của \(y=\dfrac{x^2+4}{x}\) trên \(\left(-\infty,0\right)\)
\(y=x+\dfrac{1}{x}-5\ge2\sqrt{\dfrac{x}{x}}-5=-3\)
\(y_{min}=-3\) khi \(x=1\)
\(y=4x^2+\dfrac{1}{2x}+\dfrac{1}{2x}-4\ge3\sqrt[3]{\dfrac{4x^2}{2x.2x}}-4=-1\)
\(y_{min}=-1\) khi \(x=\dfrac{1}{2}\)
\(y=x+\dfrac{4}{x}\Rightarrow y'=1-\dfrac{4}{x^2}=0\Rightarrow x=-2\)
\(y\left(-2\right)=-4\Rightarrow\max\limits_{x>0}y=-4\) khi \(x=-2\)
Đúng 0
Bình luận (0)
1) Tìm GTNN của \(B=2\left(\frac{x^2}{y^2}+\frac{y^2}{x^2}\right)-5\left(\frac{x}{y}+\frac{y}{x}\right)\\ \left(x,y>0\right)\)
2) Tìm GTLN và GTNN của \(C=\frac{\left(x^2-y^2\right)\left(1-x^2y^2\right)}{\left(1+x^2\right)^2\left(1+y^2\right)^2}\)
a)Tìm GTNN của \(\left(x+1\right)^2+2\left(x+1\right)^4\)
b)Tìm GTNN của \(\left(x-1\right)^4+\left(x+5\right)^4-123\)
a) GTNN = 0 khi x = -1
b) GTNN = 503 khi x =0
Đúng 0
Bình luận (3)
Tìm GTNN của biểu thức :
\(A=\dfrac{\left(x-1\right)\left(x+3\right)}{\left(x+2\right)^2}\)
tìm GTNN của hàm số \(f\left(x\right)=\dfrac{x^4+16}{x\left(x-2\right)\left(x+2\right)}\) với x>2
Cho 2 < x < 3. Tìm GTNN của \(P=\dfrac{1}{\left(x-2\right)^2}+\dfrac{1}{\left(3-x\right)^2}+\dfrac{1}{\left(x-2\right)\left(3-x\right)}\)
\(P\ge\dfrac{1}{2}\left(\dfrac{1}{x-2}+\dfrac{1}{3-x}\right)^2+\dfrac{4}{\left(x-2+3-x\right)^2}=\dfrac{1}{2}\left(\dfrac{1}{x-2}+\dfrac{1}{3-x}\right)^2+4\)
\(P\ge\dfrac{1}{2}\left(\dfrac{4}{x-4+3-x}\right)^2+4=12\)
Dấu "=" xảy ra khi \(x-2=3-x\Rightarrow x=\dfrac{5}{2}\)
Đúng 4
Bình luận (0)
Tìm GTNN của: \(C=\left(x^2+\dfrac{1}{y^2}\right).\left(y^2+\dfrac{1}{x^2}\right)\)
\(\text{Khai triển ra ta được: }C=x^2y^2+2+\dfrac{1}{x^2y^2}\ge2\sqrt{\dfrac{x^2y^2}{x^2y^2}}+2=4\text{ Dấu "=" xảy ra khi: }x=\pm\dfrac{1}{y}\)
Đúng 3
Bình luận (0)
Tìm GTNN của \(\sqrt{x\left(x+1\right)\left(x+2\right)\left(x+3\right)+5}\)
Tìm gtnn của biểu thức
\(A=\left|x+5\right|+\left|x+2\right|+\left|x-7\right|+\left|x-8\right|\)
Ta có tính chất :
\(\left|a\right|+\left|b\right|\ge\left|a+b\right|\)
\(\rightarrow A=\left|x+5\right|+\left|x+2\right|+\left|x-7\right|+\left|x-8\right|\ge\left|x+5+x+2+x-7+x-8\right|\)
\(\rightarrow A\ge\left|4x-8\right|\)
Vì \(\left|4x-8\right|\ge0\forall x\in R\) nên :
\(\rightarrow A\ge0\forall x\in R\)
Dấu "= " xảy ra khi :
\(\left|4x-8\right|=0\) \(\Leftrightarrow4x-8=0\)
\(\Leftrightarrow x=2\)
Vậy \(A_{min}=0\Leftrightarrow x=2\)
Đúng 1
Bình luận (0)
Tìm GTNN của biểu thức: \(A=\dfrac{3\left|x+2\right|+1}{\left|x+2\right|+1}\)