 giúp iem vs ạk
giúp iem vs ạk

Những câu hỏi liên quan
Chúng ta cần làm gì để bảo vệ môi trường?
#giúp iem với ạk
refer
Dọn dẹp vệ sinh lớp học, khuôn viên nhà ởVứt rác đúng nơi quy định, không xả rác bừa bãi.Hạn chế sử dụng túi nilon.Tiết kiệm điện, nước trong sinh hoạt.Tích cực trồng cây xanh.Hăng hái tham gia các phong trào bảo vệ môi trường.Không tiếp tay cho hành vi tổn hại đến môi trường.
Đúng 2
Bình luận (0)
REFER
Dọn dẹp vệ sinh lớp học, khuôn viên nhà ở
Vứt rác đúng nơi quy định, không xả rác bừa bãi.
Hạn chế sử dụng túi nilon.
Tiết kiệm điện, nước trong sinh hoạt.
Tích cực trồng cây xanh.
Hăng hái tham gia các phong trào bảo vệ môi trường.
Không tiếp tay cho hành vi tổn hại đến môi trường.
Đúng 1
Bình luận (0)
- xả rác đúng nơi quy định
- hạn chế đốt rác lộ thiên
- tuyền truyền cho mọi người biết về bảo vệ môi trường
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Aj bik làm câu 1,2 thì chỉ cho iem với ạk
Bà con ơi giúp iem vs ạ
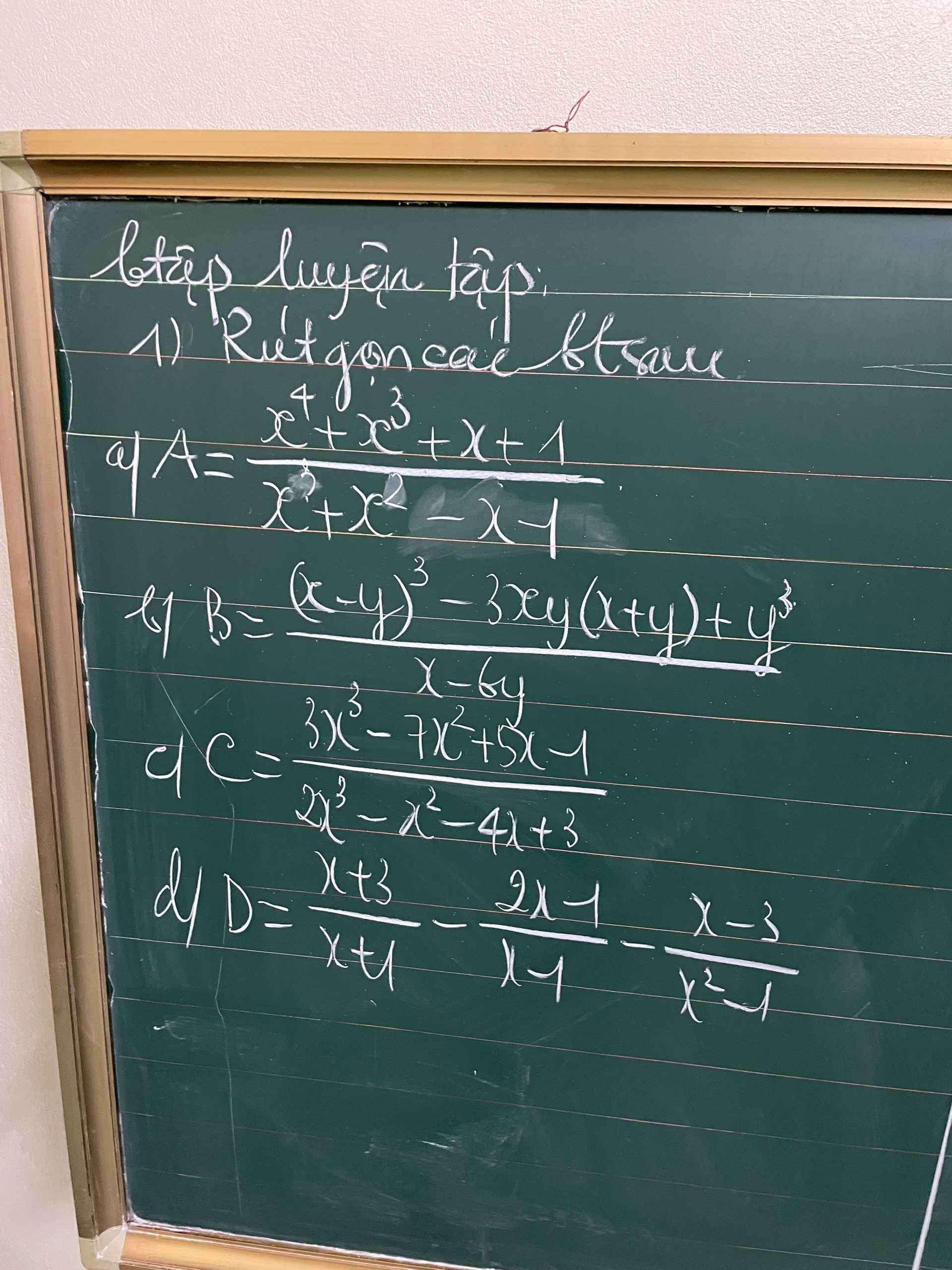
\(A=\dfrac{x^3\left(x+1\right)+\left(x+1\right)}{x^2\left(x+1\right)-\left(x+1\right)}=\dfrac{\left(x^3+1\right)\left(x+1\right)}{\left(x^2-1\right)\left(x+1\right)}\)
\(=\dfrac{x^3+1}{x^2-1}=\dfrac{\left(x+1\right)\left(x^2-x+1\right)}{\left(x+1\right)\left(x-1\right)}=\dfrac{x^2-x+1}{x-1}\)
Đúng 1
Bình luận (0)
Lời giải:
b.
$B=\frac{x^3-3x^2y+3xy^2-y^3-3x^2y-3xy^2+y^3}{x-6y}$
$=\frac{x^3-6x^2y}{x-6y}=\frac{x^2(x-6y)}{x-6y}=x^2$
c.
$C=\frac{(3x-1)(x-1)^2}{(2x+3)(x-1)^2}=\frac{3x-1}{2x+3}$
d.
$D=\frac{(x+3)(x-1)-(2x-1)(x+1)}{(x+1)(x-1)}-\frac{x-3}{(x-1)(x+1)}$
$=\frac{-x^2+1}{(x-1)(x+1)}=\frac{-(x^2-1)}{x^2-1}=-1$
Đúng 1
Bình luận (0)
giúp iem với, tìm đkxđ vs ạ, thanks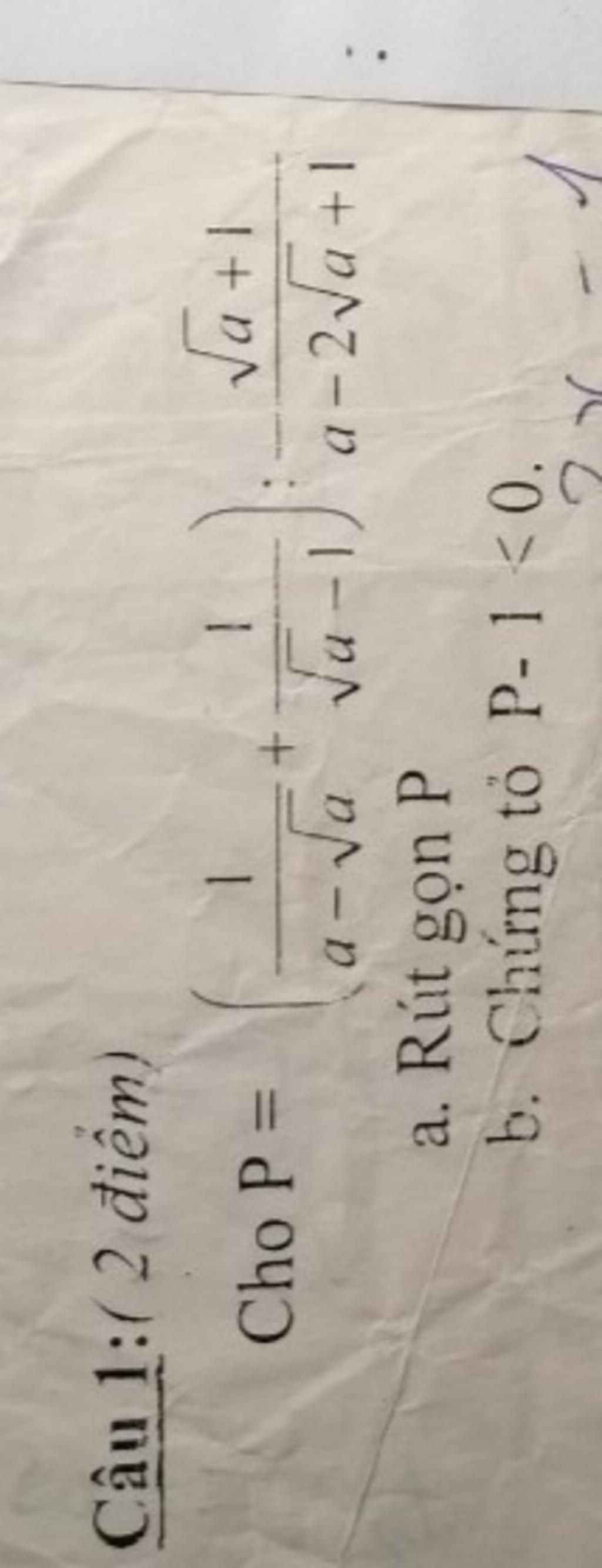
a: \(P=\dfrac{\sqrt{a}+1}{\sqrt{a}\left(\sqrt{a}-1\right)}\cdot\dfrac{\left(\sqrt{a}-1\right)^2}{\sqrt{a}+1}=\dfrac{\sqrt{a}-1}{\sqrt{a}}\)
b: \(P-1=\dfrac{\sqrt{a}-1-\sqrt{a}}{\sqrt{a}}=\dfrac{-1}{\sqrt{a}}< 0\)
Đúng 0
Bình luận (0)
giúp iem vs
√(4x^2-12x+9)=7
\(\Leftrightarrow\sqrt{\left(2x-3\right)^2}=7\\ \Leftrightarrow\left|2x-3\right|=7\\ \Leftrightarrow\left[{}\begin{matrix}2x-3=7\\3-2x=7\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=5\\x=-2\end{matrix}\right.\)
Đúng 0
Bình luận (0)
bài ni là giải phương trình nhoa
Đúng 0
Bình luận (0)
A = { xEN*| 30 ![]() ≤ x < 40}
≤ x < 40}
giúp iem vs
A = { 30;31;32;33;34;35;36;37;38;39 }
dễ
Đúng 0
Bình luận (0)

Giúp mk vs ạk
\(4Al + 3O_2 \xrightarrow{t^o} 2Al_2O_3\\ 2Al + 3Cl_2 \xrightarrow{t^o} 2AlCl_3\\ Al_2O_3 + 6HCl \to 2AlCl_3 + 3H_2O\\ Al_2O_3 + 3H_2SO_4 \to Al_2(SO_4)_3 + 3H_2O\\ AlCl_3 + 3AgNO_3 \to 3AgCl + Al(NO_3)_3\\ Al_2(SO_4)_3 + 3Ba(NO_3)_2 \to Al(NO_3)_2 + 3BaSO_4\\ Al_2(SO_4)_3 + 6KOH \to 2Al(OH)_3 + 3K_2SO_4\\ Al(NO_3)_3 + 3KOH \to Al(OH)_3 + 3KNO_3\\ Al(OH)_3 + NaOH \to NaAlO_2 + 2H_2O\\ 2Al(OH)_3 \xrightarrow{t^o} Al_2O_3 + 3H_2O\)
Đúng 3
Bình luận (0)
4Al + 3O2 -> 2Al2O3
Al2O3 + 6HCl -> 2AlCl3 + 3H2O
2Al + 6HCl -> 2AlCl3 + 3H2
Al2O3 + 3H2SO4 -> Al2(SO4)3 + 3H2O
AlCl3 + 3AgNO3 -> Al(NO3)3 + 3AgCl
Al2(SO4)3 + 3Ba(NO3)2 -> 2Al(NO3)3 + 3BaSO4
Al(NO3)3 + 3NaOHvừa đủ -> Al(OH)3 + 3NaNO3
Al2(SO4)3 + 3Ba(OH)2vừa đủ -> 2Al(OH)3 + 3BaSO4
Al(OH)3 + NaOH -> NaAlO2 + 2H2O
2Al(OH)3 -> Al2O3 + 3H2O
Al2O3 + 2NaOH -> 2NaAlO2 + H2O
Đúng 2
Bình luận (0)
\(4Al+3O_2\underrightarrow{^{t^0}}2Al_2O_3\)
\(2Al+6HCl\rightarrow2AlCl_3+3H_2\)
\(Al_2O_3+6HCl\rightarrow2AlCl_3+3H_2O\)
\(Al_2O_3+3H_2SO_4\rightarrow Al_2\left(SO_4\right)_3+3H_2\)
\(AlCl_3+3AgNO_3\rightarrow Al\left(NO_3\right)_3+3AgCl\)
\(Al_2\left(SO_4\right)_3+3Ba\left(NO_3\right)_2\rightarrow2Al\left(NO_3\right)_3+3BaSO_4\)
\(Al_2\left(SO_4\right)_3+6NaOH\rightarrow2Al\left(OH\right)_3+2Na_2SO_4\)
\(Al\left(NO_3\right)_3+3NaOH\rightarrow Al\left(OH\right)_3+3NaNO_3\)
\(NaOH+Al\left(OH\right)_3\rightarrow NaAlO_2+2H_2O\)
\(2Al\left(OH\right)_3\underrightarrow{^{t^0}}Al_2O_3+3H_2O\)
\(2NaOH+Al_2O_3\rightarrow2NaAlO_2+H_2O\)
Đúng 1
Bình luận (1)
Giúp mik vs ạk 
a) Xét \(\Delta ABC\) vuông tại A:
\(BC^2=AB^2+AC^2\left(Pytago\right).\\ \Rightarrow BC^2=4^2+3^2.\\ \Leftrightarrow BC^2=25.\\\Leftrightarrow BC=5\left(BC>0\right). \)
b) Xét \(\Delta ABD\) và \(\Delta ABC\):
AD = AC (gt).
\(\widehat{DAB}=\widehat{CAB}\left(=90^o\right).\)
AD chung.
\(\Rightarrow\Delta ABD=\Delta ABC\left(c-g-c\right).\)
\(\Rightarrow\widehat{ADB}=\widehat{ACB}\) (2 góc tương ứng).
\(\Rightarrow\Delta BDC\) cân tại B.
Đúng 1
Bình luận (0)
giúp mik vs ạk
a) Ta có: BC+CN=BN(C nằm giữa B và N)
CB+BM=CM(B nằm giữa C và M)
mà BM=CN(gt)
nên BN=CM
Xét ΔABN và ΔACM có
AB=AC(ΔABC cân tại A)
\(\widehat{ABN}=\widehat{ACM}\)(hai góc ở đáy của ΔABC cân tại A)
BN=CM(cmt)
Do đó: ΔABN=ΔACM(c-g-c)
b) Ta có: \(\widehat{ABC}+\widehat{ABM}=180^0\)(hai góc kề bù)
\(\widehat{ACB}+\widehat{ACN}=180^0\)(hai góc kề bù)
mà \(\widehat{ABC}=\widehat{ACB}\)(hai góc ở đáy của ΔABC cân tại A)
nên \(\widehat{ABM}=\widehat{ACN}\)
Xét ΔABM và ΔACN có
AB=AC(ΔABC cân tại A)
\(\widehat{ABM}=\widehat{ACN}\)(cmt)
BM=CN(gt)
Do đó: ΔABM=ΔACN(c-g-c)
c) Ta có: ΔABM=ΔACN(cmt)
nên \(\widehat{AMB}=\widehat{ANC}\)(hai góc tương ứng)
hay \(\widehat{HMB}=\widehat{KNC}\)
Xét ΔHBM vuông tại H và ΔKCN vuông tại K có
BM=CN(gt)
\(\widehat{HMB}=\widehat{KNC}\)(cmt)
Do đó: ΔHBM=ΔKCN(cạnh huyền-góc nhọn)
Suy ra: HB=KC(hai cạnh tương ứng)
d) Ta có: ΔABM=ΔACN(cmt)
nên AM=AN(hai cạnh tương ứng)
Ta có: AH+HM=AM(H nằm giữa A và M)
AK+KB=AN(K nằm giữa A và N)
mà AM=AN(cmt)
và HM=KB(cmt)
nên AH=AK
Xét ΔAHK có AH=AK(cmt)
nên ΔAHK cân tại A(Định nghĩa tam giác cân)
Xét ΔAMN có AM=AN(cmt)
nên ΔAMN cân tại A(Định nghĩa tam giác cân)
Ta có: ΔAHK cân tại A(cmt)
nên \(\widehat{AHK}=\dfrac{180^0-\widehat{HAK}}{2}\)(Số đo của một góc ở đáy trong ΔAHK cân tại A)
hay \(\widehat{AHK}=\dfrac{180^0-\widehat{MAN}}{2}\)(1)
Ta có: ΔAMN cân tại A(cmt)
nên \(\widehat{AMN}=\dfrac{180^0-\widehat{MAN}}{2}\)(Số đo của một góc ở đáy trong ΔAMN cân tại A)(2)
Từ (1) và (2) suy ra \(\widehat{AHK}=\widehat{AMN}\)
mà \(\widehat{AHK}\) và \(\widehat{AMN}\) là hai góc ở vị trí đồng vị
nên HK//MN(Dấu hiệu nhận biết hai đường thẳng song song)
hay HK//BC(Đpcm)
e) Ta có: ΔHBM=ΔKCN(cmt)
nên \(\widehat{HBM}=\widehat{KCN}\)(hai góc tương ứng)
mà \(\widehat{HBM}=\widehat{OBC}\)(hai góc đối đỉnh)
và \(\widehat{KCN}=\widehat{OCB}\)(hai góc đối đỉnh)
nên \(\widehat{OBC}=\widehat{OCB}\)
Xét ΔOBC có \(\widehat{OBC}=\widehat{OCB}\)(cmt)
nên ΔOBC cân tại O(Định nghĩa tam giác cân)
Xét ΔAHK có AH=AK(cmt)
nên ΔAHK cân tại A(Định nghĩa tam giác cân)
f) Ta có: AB=AC(ΔABC cân tại A)
nên A nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(3)
Ta có: OB=OC(ΔOBC cân tại O)
nên O nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(4)
Từ (3) và (4) suy AO là đường trung trực của BC
hay AO\(\perp\)BC(Đpcm)
Đúng 1
Bình luận (0)
































