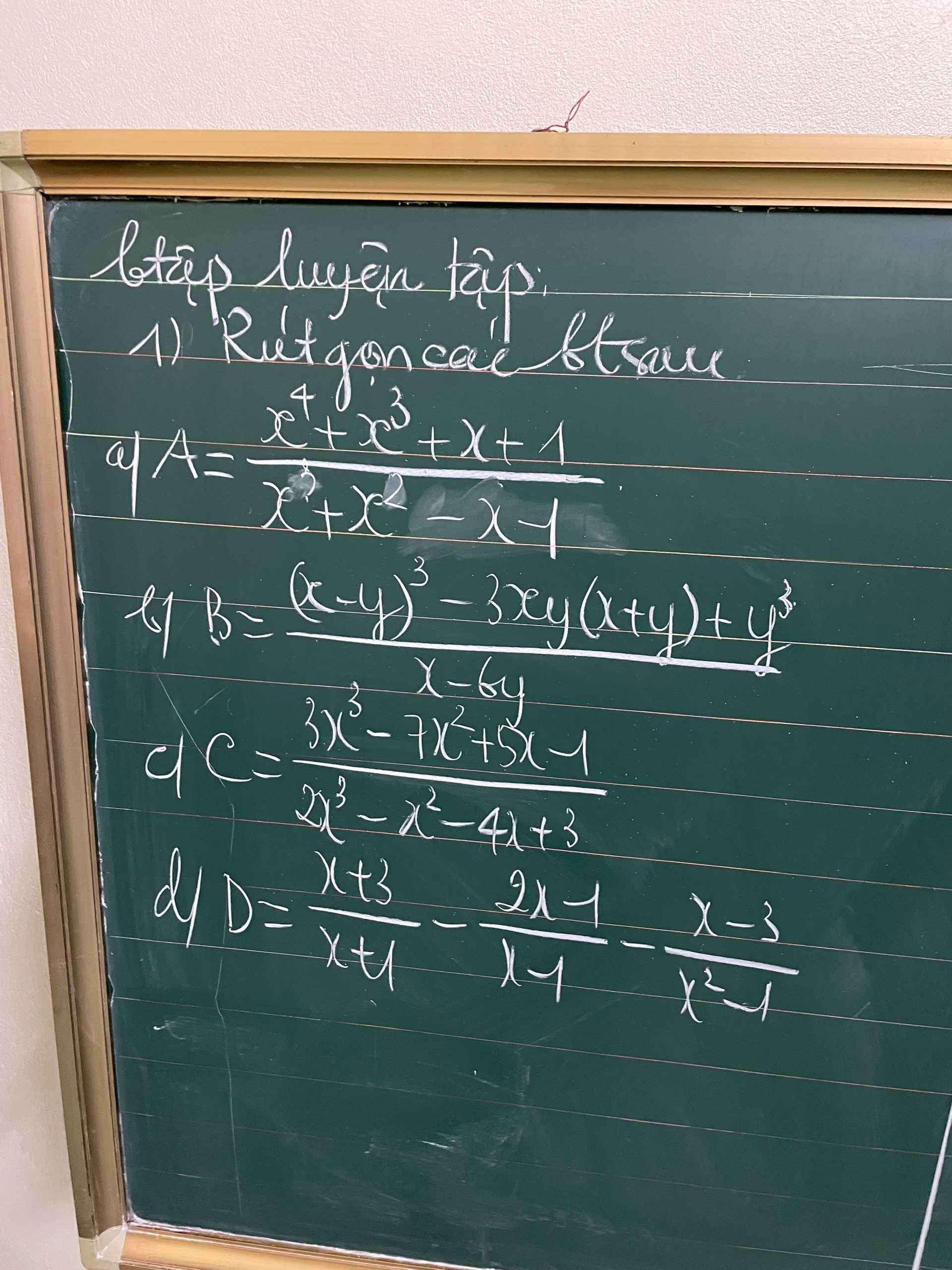\(A=\dfrac{x^3\left(x+1\right)+\left(x+1\right)}{x^2\left(x+1\right)-\left(x+1\right)}=\dfrac{\left(x^3+1\right)\left(x+1\right)}{\left(x^2-1\right)\left(x+1\right)}\)
\(=\dfrac{x^3+1}{x^2-1}=\dfrac{\left(x+1\right)\left(x^2-x+1\right)}{\left(x+1\right)\left(x-1\right)}=\dfrac{x^2-x+1}{x-1}\)
Lời giải:
b.
$B=\frac{x^3-3x^2y+3xy^2-y^3-3x^2y-3xy^2+y^3}{x-6y}$
$=\frac{x^3-6x^2y}{x-6y}=\frac{x^2(x-6y)}{x-6y}=x^2$
c.
$C=\frac{(3x-1)(x-1)^2}{(2x+3)(x-1)^2}=\frac{3x-1}{2x+3}$
d.
$D=\frac{(x+3)(x-1)-(2x-1)(x+1)}{(x+1)(x-1)}-\frac{x-3}{(x-1)(x+1)}$
$=\frac{-x^2+1}{(x-1)(x+1)}=\frac{-(x^2-1)}{x^2-1}=-1$