chứng minh bất đẳng thức sau
x2 + 6x +9 > 0
x2 + 6x + 10 > 1
Những câu hỏi liên quan
Dùng định nghĩa hai phân thức bằng nhau chứng minh các đẳng thức sau:
3
-
x
3
+
x
x
2
-
6
x
+
9
9
-
x
2
Đọc tiếp
Dùng định nghĩa hai phân thức bằng nhau chứng minh các đẳng thức sau:
3 - x 3 + x = x 2 - 6 x + 9 9 - x 2
Ta có:
3 - x . 9 - x 2 = 3 - x 3 - x 3 + x = 3 - x 2 1)
Và 3 + x x 2 - 6 x + 9 = 3 + x . x - 3 2 = 3 + x . 3 - x 2 (2)
( vì ( x- 3) = - (3- x) nên x - 3 2 = - 3 - x 2 = 3 - x 2 )
Từ (1) và (2) suy ra: x - 3 . 9 - x 2 = 3 + x x 2 - 6 x + 9
Do đó: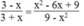 
Đúng 0
Bình luận (0)
Bài 6: a)Tìm GTLN, GTNN của biểu thức sau:a. x2 – 6x +11 b. –x2 + 6x – 11 c) Chứng minh rằng: x2 + 2x + 2 0 với x Z
Đọc tiếp
Bài 6: a)Tìm GTLN, GTNN của biểu thức sau:
a. x2 – 6x +11 b. –x2 + 6x – 11
c) Chứng minh rằng: x2 + 2x + 2 > 0 với x 
c: \(=\left(x+1\right)^2+1>0\forall x\)
Đúng 0
Bình luận (0)
Trả lời:
a, \(x^2-6x+11=x^2-6x+9+2=\left(x-3\right)^2+2\ge2\forall x\)
Dấu "=" xảy ra khi x - 3 = 0 <=> x = 3
Vậy GTNN của biểu thức bằng 2 khi x = 3
b, \(-x^2+6x-11=-\left(x^2-6x+11\right)=-\left(x^2-6x+9+2\right)=-\left[\left(x-3\right)^2+2\right]\)
\(=-\left(x-3\right)^2-2\le-2\forall x\)
Dấu "=" xảy ra khi x - 3 = 0 <=> x = 3
Vậy GTLN của biểu thức bằng - 2 khi x = 3
c, \(x^2+2x+2=x^2+2x+1+1=\left(x+1\right)^2+1\ge1>0\forall x\inℤ\) (đpcm)
Dấu "=" xảy ra khi x + 1 = 0 <=> x = - 1
Chứng minh bất đẳng thức : A = 31x ^4 -6x + 17 > 0
Chứng minh đẳng thức, bất đẳng thức: \(9x^2-6x+2>0\) với mọi x
Lời giải:
Ta thấy:
$9x^2-6x+2=(9x^2-6x+1)+1$
$=[(3x)^2-2.3x+1^2]+1=(3x-1)^2+1$
Vì $(3x-1)^2\geq 0$ với mọi $x$
$\Rightarrow 9x^2-6x+2=(3x-1)^2+1\geq 1>0$ với mọi $x$
Ta có đpcm.
Đúng 0
Bình luận (0)
Chứng minh bất đẳng thức sau: 6x4 - 18x3 + 23x2 - 13x + 4 > 0
Bài này đơn giản thôi.
Đặt f(x) = 6x4 - 18x3 + 23x2 - 13x + 4 > 0
\(f\left(x\right)=\frac{47}{54}+\frac{1}{54}\left(18x^2-27x+13\right)^2+\frac{5}{6}x^2\)
Thao tác trên Maple (vào thống kê hỏi đáp xem ảnh)
Còn cách phân tích bằng tay thì qua VMF có bài viết của mình nói về điều này nhé.
Chứng minh các đẳng thức sau:
x
6
x
+
2
x
3
+
6
x
:
6
x
2
1
3
v...
Đọc tiếp
Chứng minh các đẳng thức sau: x 6 x + 2 x 3 + 6 x : 6 x = 2 1 3 v ớ i x > 0
Chứng minh các đẳng thức sau:
x
6
x
+
2
x
3
+
6
x
:
6
x
2
1
3
v...
Đọc tiếp
Chứng minh các đẳng thức sau: x 6 x + 2 x 3 + 6 x : 6 x = 2 1 3 v ớ i x > 0
Chứng minh các phân thức sau luôn xác định với mọi x
x 2 + 2 x + 3 - 12 + 6 x - x 2
1) tìm giá trị nhỏ nhất của
D= 4x-x2+3
E=2x-2x2-5
F=-x2-4x+20
2) chứng minh biểu thức không phụ vào biến
A= (2x+3)(4x2-6x+9)-2(4x3-1)
B=(x+3)3-(x+9)(x2+27)
1. Đề bài sai, các biểu thức này chỉ có giá trị lớn nhất, không có giá trị nhỏ nhất
2.
\(A=\left(2x\right)^3-3^3-\left(8x^3+2\right)\)
\(=8x^3-27-8x^3-2\)
\(=-29\)
\(B=x^3+9x^2+27x+27-\left(x^3+9x^2+27x+243\right)\)
\(=27-243=-216\)
Đúng 2
Bình luận (0)
sửa đề lại thành tìm Max nhé1, vì mấy ý này ko có min
\(1,=>D=-\left(x^2-4x-3\right)=-\left(x^2-2.2x+4-7\right)\)
\(=-[\left(x-2\right)^2-7]=-\left(x-2\right)^2+7\le7\)
dấu"=" xảy ra<=>x=2
2, \(E=-2\left(x^2-x+\dfrac{5}{2}\right)=-2[x^2-2.\dfrac{1}{2}x+\dfrac{1}{4}+\dfrac{9}{4}]\)
\(=-2[\left(x-\dfrac{1}{2}\right)^2+\dfrac{9}{4}]\le-\dfrac{9}{2}\) dấu"=" xảy ra<=>x=1/2
3, \(F=-\left(x^2+4x-20\right)=-\left(x^2+2.2x+4-24\right)\)
\(=-[\left(x+2\right)^2-24]\le24\) dấu"=" xảy ra<=>x=-2
Đúng 2
Bình luận (0)
Bài 1:
a) Ta có: \(D=-x^2+4x+3\)
\(=-\left(x^2-4x-3\right)\)
\(=-\left(x^2-4x+4-7\right)\)
\(=-\left(x-2\right)^2+7\le7\forall x\)
Dấu '=' xảy ra khi x=2
c) Ta có: \(F=-x^2-4x+20\)
\(=-\left(x^2+4x-20\right)\)
\(=-\left(x^2+4x+4-24\right)\)
\(=-\left(x+2\right)^2+24\le24\forall x\)
Dấu '=' xảy ra khi x=-2
Đúng 0
Bình luận (0)
Xem thêm câu trả lời