làm giúp mình bài 3 và 4

Những câu hỏi liên quan
Chứng minh rằng: \(\frac{1}{3}+\frac{2}{3^2}+\frac{3}{3^3}+\frac{4}{3^4}+...+\frac{100}{3^{100}}< \frac{3}{4}\)
làm giúp mình bài này và cho mình vài bài giống như bài này đc ko !!!!!!!
Đặt \(A=\frac{1}{3}+\frac{2}{3^2}+\frac{3}{3^3}+\frac{4}{3^4}+...+\frac{100}{3^{100}}\)
\(3A=1+\frac{2}{3}+\frac{3}{3^2}+\frac{4}{3^3}+...+\frac{100}{3^{99}}\)
\(3A-A=\left(1+\frac{2}{3}+\frac{3}{3^2}+\frac{4}{3^3}+...+\frac{100}{3^{99}}\right)-\left(\frac{1}{3}+\frac{2}{3^2}+\frac{3}{3^3}+\frac{4}{3^4}+...+\frac{100}{3^{100}}\right)\)
\(2A=1+\frac{1}{3}+\frac{1}{3^2}+\frac{1}{3^3}+...+\frac{1}{3^{99}}-\frac{100}{3^{100}}\)
\(6A=3+1+\frac{1}{3}+\frac{1}{3^2}+...+\frac{1}{3^{98}}-\frac{100}{3^{99}}\)
\(6A-2A=\left(3+1+\frac{1}{3}+\frac{1}{3^2}+...+\frac{1}{3^{98}}-\frac{100}{3^{99}}\right)-\left(1+\frac{1}{3}+\frac{1}{3^2}+\frac{1}{3^3}+...+\frac{1}{3^{99}}-\frac{100}{3^{100}}\right)\)
\(4A=3-\frac{100}{3^{99}}-\frac{1}{3^{99}}+\frac{100}{3^{100}}\)
\(4A=3-\frac{300}{3^{100}}-\frac{3}{3^{100}}+\frac{100}{3^{100}}\)
\(4A=3-\frac{203}{3^{100}}< 3\)
\(A< \frac{3}{4}\left(đpcm\right)\)
1 số bài toán tương tự:CMR: \(\frac{1}{4}+\frac{2}{4^2}+\frac{3}{4^3}+\frac{4}{4^4}+...+\frac{100}{4^{100}}< \frac{4}{9}\)
Dạng tổng quát: CMR: \(\frac{1}{k}+\frac{2}{k^2}+\frac{3}{k^3}+\frac{4}{k^4}+...+\frac{n}{k^n}< \frac{k}{\left(k-1\right)^2}\)(k;n \(\in\) N*; k > 1)
Đúng 0
Bình luận (0)
Làm cho mình bài 2 và 3 nhé!
Làm nhanh giúp mình nhé!!!
Làm giúp mình bài 4 và 5 với nhé 
Làm giúp mình với nhé, nếu bạn nào mà không trả lời mình thì mình sẽ không kết bạn còn nếu giúp mình nhì mình sẽ làm bạn với bạn đó 😥
Đúng 1
Bình luận (0)
Bạn nào trả lời được thì mình sẽ bấm đúng nhé 😀
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Xem bài viết Facebook và đóng góp share, like tại: Cuộc thi Trí tuệ VICE - Bài viết | Facebook giúp chúng mình nha!
(3-4 điểm thưởng/ý làm)

các bạn khác k làm thì đừng cmt vô đây mấy bài của các bạn giải bị trôi
Đúng 4
Bình luận (1)
1, \(\)BDT AM-GM
\(=>\sqrt{a^2+b^2}\ge\sqrt{2ab}\left(1\right)\)
tương tuqj \(=>\sqrt{b^2+c^2}\ge\sqrt{2bc}\left(2\right)\)
\(=>\sqrt{c^2+a^2}\ge\sqrt{2ac}\left(3\right)\)
cộng vế (1)(2)(3)
\(=>Vt=\sqrt{2}\left(\sqrt{ab}+\sqrt{bc}+\sqrt{ac}\right)=\sqrt{2021}\)
\(=>\sqrt{ab}+\sqrt{bc}+\sqrt{ca}=\dfrac{\sqrt{2021}}{\sqrt{2}}\)
\(=>\sqrt{ab}+\sqrt{bc}+\sqrt{ac}\le a+b+c\)\(=>a+b+C\ge\dfrac{\sqrt{2021}}{\sqrt{2}}\)
đặt \(P=\dfrac{a^2}{b+c}+\dfrac{b^2}{c+a}+\dfrac{c^2}{a+b}\)
\(=>P\ge\dfrac{\left(a+b+c\right)^2}{2\left(a+b+c\right)}=\dfrac{a+b+c}{2}=\dfrac{1}{2}.\dfrac{\sqrt{2021}}{\sqrt{2}}\)
dấu"=" xảy ra<=>\(a=b=c=\dfrac{\sqrt{2021}}{3\sqrt{2}}\)
Đúng 1
Bình luận (1)
Xem thêm câu trả lời
Xem bài viết Facebook và đóng góp share, like tại: Cuộc thi Trí tuệ VICE - Bài viết | Facebook giúp chúng mình nha! (3-4 điểm thưởng/ý làm)
Đọc tiếp
Xem bài viết Facebook và đóng góp share, like tại: Cuộc thi Trí tuệ VICE - Bài viết | Facebook giúp chúng mình nha!

 (3-4 điểm thưởng/ý làm)
(3-4 điểm thưởng/ý làm)
C7, \(\dfrac{\left(b+c\right)\left(a^2+bc\right)}{b^2+bc+c^2}\ge\dfrac{\left(2\sqrt{bc}\right).\left(2a\sqrt{bc}\right)}{3\sqrt[3]{b^2.bc.c^2}}=\dfrac{4abc}{3abc}=\dfrac{4}{3}\left(1\right)\)
tương tự \(=>\dfrac{\left(a+c\right)\left(b^2+Ac\right)}{a^2+ac+c^2}\ge\dfrac{4}{3}\left(2\right)\)
\(=>\dfrac{\left(b+a\right)\left(c^2+ba\right)}{a^2+ab+b^2}\ge\dfrac{4}{3}\left(3\right)\)
cộng vế (1)(2)(3) \(=>P\ge4\)
dấu"=" xảy ra<=>a=b=c=1
Đúng 0
Bình luận (3)
ằng một đoạn văn khoảng 8 câu, em hãy trình bày cảm nhận của mình về nhân vật Mèo trong truyện Bức tranh của em gái tôi. Trong đoạn văn, có sử dụng một phép so sánh (yêu cầu gạch chân câu có phép so sánh đó và chú thích rõ)
Đúng 0
Bình luận (1)
Xem thêm câu trả lời

ai giúp mình làm bài 3 và bài 1 với
mik chỉ bt nhiêu đó thui, bn thông cảm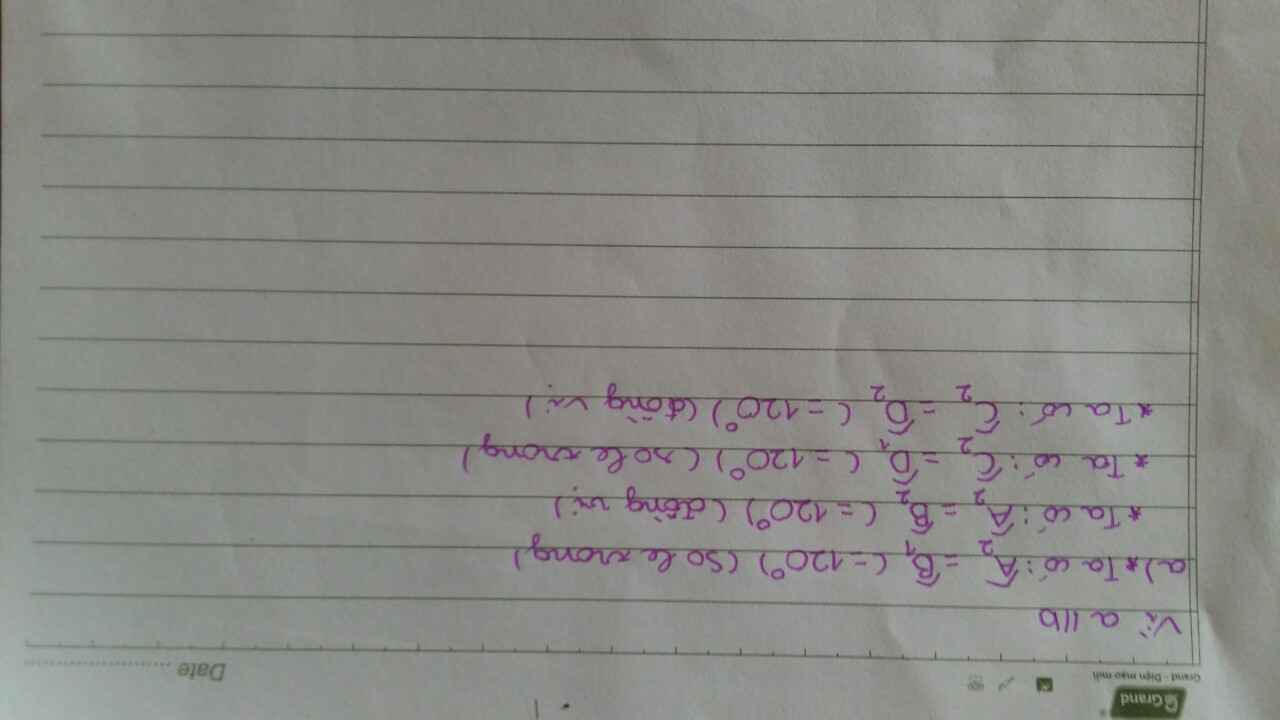
Đúng 0
Bình luận (0)
3/4-7/5+3/10 giúp mình làm bài này với mình đang gấp
\(\dfrac{3}{4}-\dfrac{7}{5}+\dfrac{3}{10}\)
\(=\dfrac{15}{20}-\dfrac{28}{20}+\dfrac{6}{20}\)
\(=\dfrac{-7}{20}\)
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
3/4-7/5+3/10 giúp mình làm bài này với mình đang gấp
`3/4 - 7/5 +3/10`
`= 15/20 - 28/20 +6/20`
`=(15-28+6)/20`
`=-7/20`
Đúng 2
Bình luận (1)
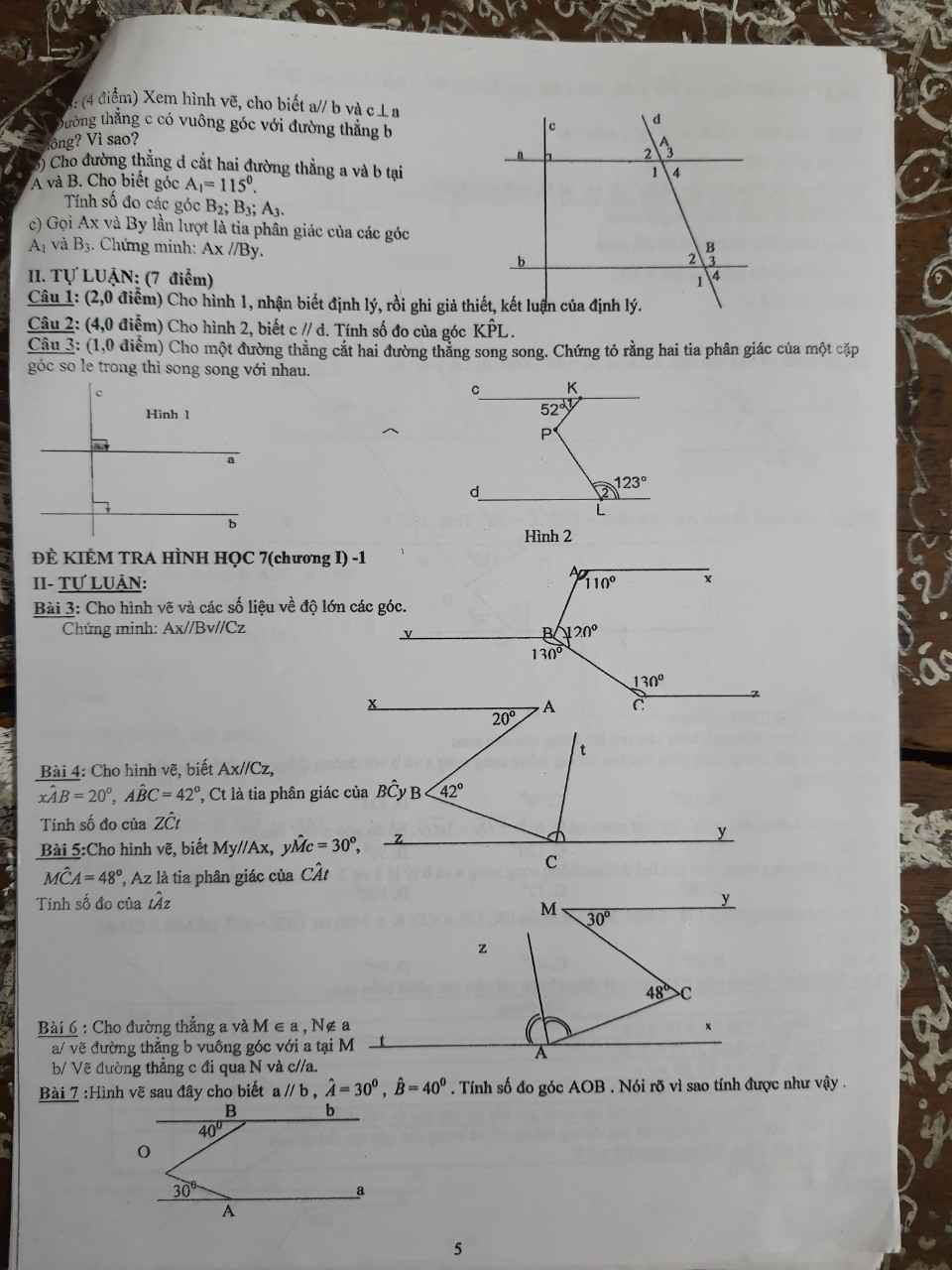
ai giúp mình làm hai bài 3 và bài 7 với
























