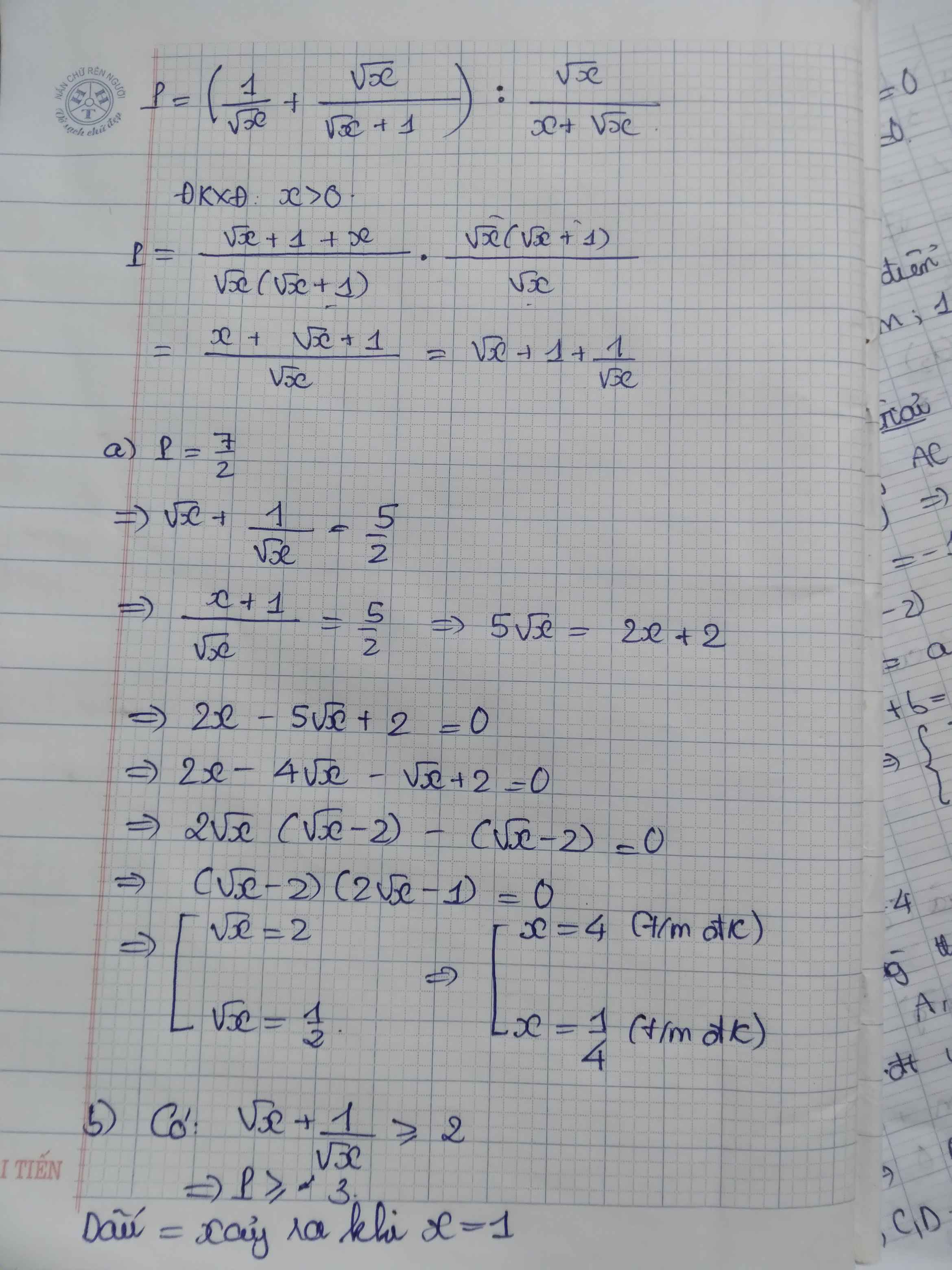Tìm giá trị nhỏ nhất: \(\dfrac{2\left|x-1\right|+11}{\left|x-1\right|+7}\)

Những câu hỏi liên quan
Tìm giá trị nhỏ nhất :
\(D=\left|x-\dfrac{1}{2}\right|+\left|x-\dfrac{1}{3}\right|+\left|x-\dfrac{1}{4}\right|+...+\left|x-\dfrac{1}{2022}\right|\)
Bài 1 : cho biểu thức
\(p=\left(\dfrac{1}{\sqrt{x}-1}+\dfrac{\sqrt{x}}{x-1}\right):\left(\dfrac{\sqrt{x}}{\sqrt{x}-1}-1\right)\) với x lớn hơn hoặc bằng 0 ; x # 1
1) rút gọ P
2 tìm x để P = \(\dfrac{7}{4}\)
tìm giá trị nhỏ nhất của p
1, Với \(x\ge0,x\ne1\) ta có :
\(P=\left(\dfrac{1}{\sqrt{x}-1}+\dfrac{\sqrt{x}}{x-1}\right):\left(\dfrac{\sqrt{x}}{\sqrt{x}-1}-1\right)\)
\(=\dfrac{\sqrt{x}+1+\sqrt{x}}{x-1}:\dfrac{\sqrt{x}-\sqrt{x}+1}{\sqrt{x}-1}\)
\(=\dfrac{\left(2\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{2\sqrt{x}+1}{\sqrt{x}+1}\)
2, Ta có \(P=\dfrac{7}{4}\)
\(\Rightarrow\dfrac{2\sqrt{x}+1}{\sqrt{x}+1}=\dfrac{7}{4}\)
\(\Leftrightarrow4\left(2\sqrt{x}+1\right)=7\left(\sqrt{x}+1\right)\)
\(\Leftrightarrow8\sqrt{x}+4=7\sqrt{x}=7\)
\(\Leftrightarrow\sqrt{x}=3\)
\(\Leftrightarrow x=9\left(tm\right)\)
Đúng 0
Bình luận (0)
1) Ta có: \(P=\left(\dfrac{1}{\sqrt{x}-1}+\dfrac{\sqrt{x}}{x-1}\right):\left(\dfrac{\sqrt{x}}{\sqrt{x}-1}-1\right)\)
\(=\left(\dfrac{\sqrt{x}+1+\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right):\left(\dfrac{\sqrt{x}}{\sqrt{x}-1}-\dfrac{\sqrt{x}-1}{\sqrt{x}-1}\right)\)
\(=\dfrac{2\sqrt{x}+1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\cdot\dfrac{\sqrt{x}-1}{\sqrt{x}-\sqrt{x}+1}\)
\(=\dfrac{2\sqrt{x}+1}{\sqrt{x}+1}\)
2) Để \(P=\dfrac{7}{4}\) thì \(\dfrac{2\sqrt{x}+1}{\sqrt{x}+1}=\dfrac{7}{4}\)
\(\Leftrightarrow4\cdot\left(2\sqrt{x}+1\right)=7\left(\sqrt{x}+1\right)\)
\(\Leftrightarrow8\sqrt{x}+4=7\sqrt{x}+7\)
\(\Leftrightarrow8\sqrt{x}-7\sqrt{x}=7-4\)
\(\Leftrightarrow\sqrt{x}=3\)
hay x=9(nhận)
Vậy: Để \(P=\dfrac{7}{4}\) thì x=9
Đúng 0
Bình luận (0)
1. Cho số nguyên dương x, tìm giá trị nhỏ nhất của biểu thức:Pdfrac{left(x+1right)^6}{left(x^3+7right)left(x^3+3x^2+4right)}. 2. Cho a,bge0 thỏa mãn a-sqrt{a}sqrt{b}-b, tìm giá trị nhỏ nhất của biểu thức:Mleft(a-bright)left(a+b-1right). 3. Cho Delta OEF vuông tại O có OEa, OFb, EFc và widehat{OEF}alpha, widehat{OFE}beta.1)i, Chứng minh rằng không có giá trị nào của a,b,c để biểu thức Adfrac{a+b}{c}+dfrac{c}{a+b} nhận giá trị nguyên.ii, Giả sử csqrt{ab}sqrt{2} , tìm giá trị nhỏ nhất của biểu thức...
Đọc tiếp
1. Cho số nguyên dương x, tìm giá trị nhỏ nhất của biểu thức:
\(P=\dfrac{\left(x+1\right)^6}{\left(x^3+7\right)\left(x^3+3x^2+4\right)}\).
2. Cho \(a,b\ge0\) thỏa mãn \(a-\sqrt{a}=\sqrt{b}-b\), tìm giá trị nhỏ nhất của biểu thức:
\(M=\left(a-b\right)\left(a+b-1\right)\).
3. Cho \(\Delta OEF\) vuông tại O có \(OE=a\), \(OF=b\), \(EF=c\) và \(\widehat{OEF}=\alpha\), \(\widehat{OFE}=\beta\).
1)
i, Chứng minh rằng không có giá trị nào của a,b,c để biểu thức \(A=\dfrac{a+b}{c}+\dfrac{c}{a+b}\) nhận giá trị nguyên.
ii, Giả sử \(c\sqrt{ab}=\sqrt{2}\) , tìm giá trị nhỏ nhất của biểu thức \(B=\left(a+b\right)^2\).
2)
i, Tìm giá trị nhỏ nhất của biểu thức \(C=\dfrac{1}{\sin^2\alpha}+\dfrac{1}{\sin^2\beta}-2\left(\sin^2\alpha+\sin^2\beta\right)+\dfrac{\sin\alpha}{\tan\alpha}-\dfrac{\tan\alpha+\cos\beta}{\cot\beta}\) .
ii, Tìm điều kiện của \(\Delta OEF\) khi \(2\cos^2\beta-\cot^2\alpha+\dfrac{1}{\sin^2\alpha}=2\).
Tìm giá trị lớn nhất , giá trị nhỏ nhất của biểu thức :
a)\(A=\left|\dfrac{3}{5}-x\right|+\dfrac{1}{9}\)
b)B=\(\dfrac{2009}{2008}-\left|x-\dfrac{3}{5}\right|\)
c)C=\(-2\left|\dfrac{1}{3}x+4\right|+1\dfrac{2}{3}\)
Ai lm đc câu nào thì giúp mk với , cảm ơn !!
Đúng 0
Bình luận (0)
\(A=\left|\dfrac{3}{5}-x\right|+\dfrac{1}{9}\ge\dfrac{1}{9}\\ A_{min}=\dfrac{1}{9}\Leftrightarrow x=\dfrac{3}{5}\\ B=\dfrac{2009}{2008}-\left|x-\dfrac{3}{5}\right|\le\dfrac{2009}{2008}\\ B_{max}=\dfrac{2009}{2008}\Leftrightarrow x=\dfrac{3}{5}\\ C=-2\left|\dfrac{1}{3}x+4\right|+1\dfrac{2}{3}\le1\dfrac{2}{3}\\ C_{max}=1\dfrac{2}{3}\Leftrightarrow\dfrac{1}{3}x=-4\Leftrightarrow x=-12\)
Đúng 1
Bình luận (0)
a: \(A=\left|\dfrac{3}{5}-x\right|+\dfrac{1}{9}\ge\dfrac{1}{9}\forall x\)
Dấu '=' xảy ra khi \(x=\dfrac{3}{5}\)
Đúng 1
Bình luận (0)
P=\(\left(\dfrac{1}{\sqrt{x}}+\dfrac{\sqrt{x}}{\sqrt{x}+1}\right):\dfrac{\sqrt{x}}{x+\sqrt{x}}\)
1. Tìm giá trị của x để P=\(\dfrac{7}{2}\)
2. Tìm giá trị nhỏ nhất của P
1) Ta có: \(P=\left(\dfrac{1}{\sqrt{x}}+\dfrac{\sqrt{x}}{\sqrt{x}+1}\right):\dfrac{\sqrt{x}}{x+\sqrt{x}}\)
\(=\dfrac{x+\sqrt{x}+1}{\sqrt{x}\left(\sqrt{x}+1\right)}\cdot\dfrac{\sqrt{x}\left(\sqrt{x}+1\right)}{\sqrt{x}}\)
\(=\dfrac{x+\sqrt{x}+1}{\sqrt{x}}\)
Để \(P=\dfrac{7}{2}\) thì \(2x+2\sqrt{x}+2-7\sqrt{x}=0\)
\(\Leftrightarrow2x-4\sqrt{x}-\sqrt{x}+2=0\)
\(\Leftrightarrow2\sqrt{x}\left(\sqrt{x}-2\right)-\left(\sqrt{x}-2\right)=0\)
\(\Leftrightarrow\left(\sqrt{x}-2\right)\left(2\sqrt{x}-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=4\\x=\dfrac{1}{4}\end{matrix}\right.\)
Đúng 0
Bình luận (0)
Tìm giá trị lớn nhất hoặc giá trị nhỏ nhất
\(A=\dfrac{2022}{\left|x\right|+2003}\)
\(B=\left(\left|x\right|+1\right)^{10}+2009\)
a: |x|+2003>=2003
=>A<=2022/2003
Dấu = xảy ra khi x=0
b: |x|+1>=1
=>(|x|+1)^10>=1
=>B>=2010
Dấu = xảy ra khi x=0
Đúng 2
Bình luận (0)
Tìm x để biểu thức:
a) A= 0,6 + \(\left|\dfrac{1}{2}-x\right|\) đạt giá trị nhỏ nhất
b) B= \(\dfrac{2}{3}\) - \(\left|2x+\dfrac{2}{3}\right|\) đạt giá trị lớn nhất
\(A=0,6+\left|\dfrac{1}{2}-x\right|\\ Vì:\left|\dfrac{1}{2}-x\right|\ge\forall0x\in R\\ Nên:A=0,6+\left|\dfrac{1}{2}-x\right|\ge0,6\forall x\in R\\ Vậy:min_A=0,6\Leftrightarrow\left(\dfrac{1}{2}-x\right)=0\Leftrightarrow x=\dfrac{1}{2}\)
Đúng 1
Bình luận (0)
\(B=\dfrac{2}{3}-\left|2x+\dfrac{2}{3}\right|\\ Vì:\left|2x+\dfrac{2}{3}\right|\ge0\forall x\in R\\ Nên:B=\dfrac{2}{3}-\left|2x+\dfrac{2}{3}\right|\le\dfrac{2}{3}\forall x\in R\\ Vậy:max_B=\dfrac{2}{3}\Leftrightarrow\left|2x+\dfrac{2}{3}\right|=0\Leftrightarrow x=-\dfrac{1}{3}\)
Đúng 1
Bình luận (0)
Gọi \(x_1;x_2\) là hai nghiệm của phương trình \(2012x^2-\left(20a-11\right)x-2012=0\) (a là số thực). Tìm giá trị nhỏ nhất của biểu thức \(P=\dfrac{3}{2}\left(x_1-x_2\right)^2+2\left(\dfrac{x_1-x_2}{2}+\dfrac{1}{x_1}-\dfrac{1}{x_2}\right)^2\)
\(\left\{{}\begin{matrix}x_1+x_2=\dfrac{20a-11}{2012}\\x_1x_2=-1\end{matrix}\right.\)
\(P=\dfrac{3}{2}\left(x_1-x_2\right)^2+2\left(\dfrac{x_1-x_2}{2}-\dfrac{x_1-x_2}{x_1x_2}\right)^2\)
\(=\dfrac{3}{2}\left(x_1-x_2\right)^2+2\left(x_1-x_2\right)^2\left(\dfrac{1}{2}-\dfrac{1}{x_1x_2}\right)^2\)
\(=\dfrac{3}{2}\left(x_1-x_2\right)^2+2\left(x_1-x_2\right)^2\left(\dfrac{1}{2}+1\right)^2\)
\(=6\left(x_1-x_2\right)^2=6\left(x_1+x_2\right)^2-24x_1x_2\)
\(=6\left(\dfrac{20a-11}{2012}\right)^2+24\ge24\)
Dấu "=" xảy ra khi \(a=\dfrac{11}{20}\)
Đúng 1
Bình luận (0)
P = \(\left(\dfrac{2\sqrt{x}+2}{x\sqrt{x}+x-\sqrt{x}-1}+\dfrac{1}{\sqrt{x}+1}\right):\left(1-\dfrac{\sqrt{x}}{\sqrt{x}+1}\right)\)
a) Rút gọn P
b) Tìm các giá trị x nguyên để P nhận giá trị nguyên
c) Tìm giá trị nhỏ nhất của biểu thức \(\dfrac{1}{P}\)
a: \(P=\left(\dfrac{2+\sqrt{x}-1}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right):\dfrac{\sqrt{x}+1-\sqrt{x}}{\sqrt{x}+1}\)
\(=\dfrac{1}{\sqrt{x}-1}\cdot\dfrac{\sqrt{x}+1}{1}=\dfrac{\sqrt{x}+1}{\sqrt{x}-1}\)
b: Để P nguyên thì \(\sqrt{x}+1⋮\sqrt{x}-1\)
\(\Leftrightarrow\sqrt{x}-1\in\left\{-1;1;2\right\}\)
hay \(x\in\left\{0;4;9\right\}\)
Đúng 0
Bình luận (0)