Cho hàm số y = - 4 x 3 + 3 x + 2 , có đồ thị là (C). Tìm a để phương trình 4 x 3 - 3 x - 4 a 3 + 3 a = 0 có hai nghiệm âm và một nghiệm dương.
A. 0 < a < 3 2 h o ặ c 1 > a
B. - 3 2 < a < 0 h o ặ c 3 2 < a < 1
C. 1 < a < 3 2
D. 0 < a < 3 2
Những câu hỏi liên quan
Cho hàm số y=-x+3
a , vẽ đồ thị hàm số y=-x+3
b, tìm m và n để đồ thị của hai hàm số y =-x+3 và y=(2m-3) x-n là hai đường thẳng song song
c, giải hệ phương trình x + 2y=-5
3x-y=13
Xem chi tiết
Cho hàm số: \(y=x^2-3x-4\) có đồ thị là (P).
a) Lập bảng biến thiên và vẽ (P).
b) Tìm m để phương trình \(\left|x^2-3x-4\right|=2m-1\) có bốn nghiệm phân biệt.
c) Tìm m để phương trình \(x^2-3\left|x\right|-4=m\) có 3 nghiệm.
GIÚP MÌNH VỚI MÌNH ĐANG CẦN GẤP
b: \(\Leftrightarrow\left[{}\begin{matrix}x^2-3x-4=2m-1\\x^2-3x-4=-2m+1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x^2-3x-4-2m+1=0\\x^2-3x-4+2m-1=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2-3x-2m+3=0\\x^2-3x+2m-5=0\end{matrix}\right.\)
Để phương trình có bốn nghiệm phân biệt thì \(\left\{{}\begin{matrix}9-4\left(-2m+3\right)>0\\9-4\left(2m-5\right)>0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}9+8m-12>0\\9-8m+20>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}8m>3\\8m< 29\end{matrix}\right.\Leftrightarrow\dfrac{3}{8}< m< \dfrac{29}{8}\)
Đúng 0
Bình luận (0)
Cho hàm số \(y=-x^3+3x-2\) (C)
a) Khảo sát và vẽ đồ thị hàm số
b) Tìm m để phương trình: \(x^3-3x+2m+1=0\) có 3 nghiệm phân biệt
c) Viết phương trình tiếp tuyến với (C) tại điểm có hoành độ \(x=0\)
phần 1
-hệ phương trình
/
| 3 x - 4 y 7
| 2 x + Sy -1
-hàm số và đồ thị của hàm số y a x²
Đồng biến nghịch biến tìm hệ số a
vd : cho hàm số y ax² (P)
a, tìm a cho biết đồ thị hàm số đi qua A ( -3 ; 3 )
b, vẽ đồ thị hàm số với a vừa tìm được
- giải bài toán bằng hệ phương trình
- chứng minh tứ giác nội tiếp ( các điểm cùng thuộc 1 đường tròn )
- các góc bằng nhau . L là góc nội tiếp
- chứng minh bất đẳng thức
phương trình bặc nhất 2 ẩn ; nghiệ...
Đọc tiếp
phần 1 -hệ phương trình / | 3 x - 4 y = 7 < | 2 x + Sy = -1 \ -hàm số và đồ thị của hàm số y = a x² Đồng biến nghịch biến tìm hệ số a vd : cho hàm số y = ax² (P) a, tìm a cho biết đồ thị hàm số đi qua A ( -3 ; 3 ) b, vẽ đồ thị hàm số với a vừa tìm được - giải bài toán bằng hệ phương trình - chứng minh tứ giác nội tiếp ( các điểm cùng thuộc 1 đường tròn ) - các góc bằng nhau . L là góc nội tiếp - chứng minh bất đẳng thức phương trình bặc nhất 2 ẩn ; nghiệm của phương trình a x + b y = c ( Xo ; Yo ) 2 hệ tương đương khi có cùng tập nghiệm hàm số đồng biến , nghịch biến và tìm hệ số điểm thuộc đồ thị vị trí tương đối của 2 đường tròn , đường tròn ngoại tiếp của tam giác tính chất 2 tiếp tuyến cắt nhau tứ giác nối tiếp - công thức nghiệm tam giác - một mảnh vườn hình chữ nhật có nhiều dài lớn hơn chiều rộng 6m ; mảnh vườn là 160 m² tìm cách kích thước của mảnh vườn
3:
Gọi chiều rộng là x
=>Chiềudài là x+6
Theo đề, ta có: x(x+6)=160
=>x^2+6x-160=0
=>(x+16)(x-10)=0
=>x-10=0
=>x=10
=>Chiều dài là 16m
Đúng 1
Bình luận (0)
Cho hàm số
y
(
2
m
+
2
)
x
2
. Tìm m để đồ thị hàm số đi qua điểm A (x; y) với (x: y) là nghiệm của hệ phương trình:
x
−
y
1
2
x...
Đọc tiếp
Cho hàm số y = ( 2 m + 2 ) x 2 . Tìm m để đồ thị hàm số đi qua điểm A (x; y) với (x: y) là nghiệm của hệ phương trình: x − y = 1 2 x − y = 3
A. m = 7 4
B. m = 1 4
C. m = 7 8
D. m = - 7 8
Cho hàm số y = x^4 + 2(m + 1)x^2 + 1
a) Khảo sát và vẽ đồ thị khi m = 1
b) Tìm m để đồ thị hàm số có 3 điểm cực trị. Tìm phương trình đường cong đi qua các điểm cực trị đó
b.
y = x^4 + 2(m + 1)x^2 + 1
y' = 4x^3 + 4(m + 1)x
y'= 0=> x=0 và x^2 + (m + 1)= 0 (*)
để đồ thị hàm số có 3 điểm cực trị thì (*) có 2 nghiệm phân biệt
=> m+1<0
<=> m< -1
ta có:
y= [4x^3 + 4(m + 1)x]*x/4+ (m+1)x^2+ 1
y= y'*x/4+ (m+1)x^2+ 1
đường cong đi qua các điểm cực trị thỏa mãn y'= 0
=> pt phương trình đường cong đi qua các điểm cực trị đó là:
y= (m+1)x^2+ 1
Vậy để đồ thị hàm số có 3 điểm cực trị thì m< -1
và pt phương trình đường cong đi qua các điểm cực trị đó là:
y= (m+1)x^2+ 1
Đúng 0
Bình luận (0)
b.
y = x^4 + 2(m + 1)x^2 + 1
y' = 4x^3 + 4(m + 1)x
y'= 0=> x=0 và x^2 + (m + 1)= 0 (*)
để đồ thị hàm số có 3 điểm cực trị thì (*) có 2 nghiệm phân biệt
=> m+1<0
<=> m< -1
ta có:
y= [4x^3 + 4(m + 1)x]*x/4+ (m+1)x^2+ 1
y= y'*x/4+ (m+1)x^2+ 1
đường cong đi qua các điểm cực trị thỏa mãn y'= 0
=> pt phương trình đường cong đi qua các điểm cực trị đó là:
y= (m+1)x^2+ 1
Vậy để đồ thị hàm số có 3 điểm cực trị thì m< -1
và pt phương trình đường cong đi qua các điểm cực trị đó là:
y= (m+1)x^2+ 1
Đúng 0
Bình luận (0)
Cho hàm số y = f(x) = (m+1)x – 2 có đồ thị là (d)
a. Tìm m biết rằng đồ thị (d) của hàm số đi qua A(-2:0)
b. Nêu tính chất và vẽ đồ thị hàm số với m tìm được ở câu a .
c. Không tính hãy so sánh f(2√3) và f(3√2)
d. Viết phương trình đường thẳng đi qua B(-1;1)và vuông góc với (d) nói trên
: Cho hàm số : y ( m – 1).x + m (d)
a) Tìm m để hàm số đồng biến, nghịch biến ?
b) Tìm m để đồ thị hàm số đi qua điểm A( - 1 ; 1)
c) Tìm m để đồ thị hàm số song song với đường thẳng có phương trình : x – 2y 1
d) Tìm m để đồ thị hàm số cắt trục hoành tại điểm A có hoành độ x 2- căn 3 /2
Đọc tiếp
: Cho hàm số : y = ( m – 1).x + m (d)
a) Tìm m để hàm số đồng biến, nghịch biến ?
b) Tìm m để đồ thị hàm số đi qua điểm A( - 1 ; 1)
c) Tìm m để đồ thị hàm số song song với đường thẳng có phương trình : x – 2y = 1
d) Tìm m để đồ thị hàm số cắt trục hoành tại điểm A có hoành độ x = 2- căn 3 /2
Lời giải:
a. Để hàm đồng biến thì $m-1>0\Leftrightarrow m>1$
Để hàm nghịch biến thì $m-1<0\Leftrightarrow m< 1$
b. Để đths đi qua điểm $A(-1;1)$ thì:
$y_A=(m-1)x_A+m$
$\Leftrightarrow 1=(m-1)(-1)+m=1-m+m$
$\Leftrightarrow 1=1$ (luôn đúng)
Vậy đths luôn đi qua điểm A với mọi $m$
c.
$x-2y=1\Rightarrow y=\frac{1}{2}x-\frac{1}{2}$
Để đths đã cho song song với đths $y=\frac{1}{2}x-\frac{1}{2}$ thì:
\(\left\{\begin{matrix} m-1=\frac{1}{2}\\ m\neq \frac{-1}{2}\end{matrix}\right.\Leftrightarrow m=\frac{3}{2}\)
d,
ĐTHS cắt trục hoành tại điểm có hoành độ $\frac{2-\sqrt{3}}{2}$, tức là ĐTHS đi qua điểm $(\frac{2-\sqrt{3}}{2}; 0)$
$\Rightarrow 0=(m-1).\frac{2-\sqrt{3}}{2}+m$
$\Leftrightarrow m=\frac{2-\sqrt{3}}{4-\sqrt{3}}$
Đúng 0
Bình luận (0)
Cho hàm số yf(x) có đạo hàm trên
ℝ
. Đồ thị hàm số yf(x) như hình vẽ bên dưới Tìm m để bất phương trình
m
-
x
≥
2
f
x
+
2
+
4
x
+
3
nghiệm đúng với mọi
x
∈
-
3
;...
Đọc tiếp
Cho hàm số y=f(x) có đạo hàm trên ℝ . Đồ thị hàm số y=f'(x) như hình vẽ bên dưới
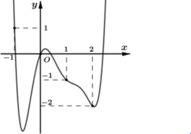
Tìm m để bất phương trình m - x ≥ 2 f x + 2 + 4 x + 3 nghiệm đúng với mọi x ∈ - 3 ; + ∞
A. m ≥ 2 f ( 0 ) - 1
B. m ≤ 2 f ( 0 ) - 1
C. m ≤ 2 f ( - 1 )
D. m ≥ 2 f ( - 1 )
Đáp án B
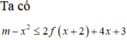
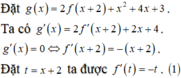
(1) là phương trình hoành độ giao điểm của đồ thị f'(t) và đường thẳng d : y = -t (hình vẽ)
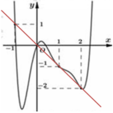
Dựa vào đồ thị của f'(t) và đường thẳng y =-t ta có
Đúng 0
Bình luận (0)
Mọi người giúp mình với ạ!!! Mình cảm ơn rất nhiều!!!
1, Viết phương trình đường thẳng đi qua các điểm cực trị của đồ thị hàm số:
\(y=x^3-6x^2-3x+2\)
2, Cho hàm số: \(y=x^3-x^2+mx\)
Tìm m để đồ thị hàm số có các điểm cực đại, cực tiểu: A, B sao cho Δ OAB vuông góc tại O.
