Cho ∫ f ( x ) d x = e 2 x - 1 x + ln x + C , x>0. Mệnh đề nào dưới đây đúng?
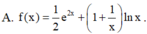
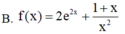
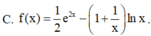
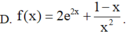
( Mu4-42. Cho hàm so $f(x)$ có đạo hàm trên đoạn $[0 ; 1]$ thỏa mãn $f(1)=0$ và $\int_0^1\left[f^{\prime}(x)\right]^2 d x=\int_0^1(x+1) e^x f(x) d x=\frac{e^2-1}{4}$. Tinh tich phân $I=\int_{0}^1 f(x) d x$.
A. $I=2-e$.
B. $I=\frac{e}{2}$.
C. $l=e-2$.
D. $1=\frac{e-1}{2}$
giúp em mấy bài nguyên hàm với ạ. huhu
1) cho f(x)=8sin bình(x+pi/12) một nguyên hàm F(x) của f(x) thỏa F(0)=8 là
A.4x+2sin(2x+pi/6)+9
B.4x-2sin(2x+pi/6)-9
C.4x+2sin(2x+pi/6)+7
D.4x-2sin(2x+pi/6)+7
2)cho f(x)=x*(e mũ -x) một nguyên hàm F(x) của f(x) thỏa F(0)=1 là
A.-(x+1) *(e mũ -x)+1
B.-(x+1)*(e mũ -x)+2
C.(x+1)*(e mũ -x)+1
D.(x+1)*(e mũ -x)+2
Lời giải:
Bài 1:
Ta nhớ công thức \(\sin^2x=\frac{1-\cos 2x}{2}\). Áp dụng vào bài toán:
\(F(x)=8\int \sin^2\left(x+\frac{\pi}{12}\right)dx=4\int \left [1-\cos \left(2x+\frac{\pi}{6}\right)\right]dx\)
\(\Leftrightarrow F(x)=4\int dx-4\int \cos \left(2x+\frac{\pi}{6}\right)dx=4x-2\int \cos (2x+\frac{\pi}{6})d(2x+\frac{\pi}{6})\)
\(\Leftrightarrow F(x)=4x-2\sin (2x+\frac{\pi}{6})+c\)
Giải thích 1 chút: \(d(2x+\frac{\pi}{6})=(2x+\frac{\pi}{6})'dx=2dx\)
Vì \(F(0)=8\Rightarrow -1+c=8\Rightarrow c=9\)
\(\Rightarrow F(x)=4x-2\sin (2x+\frac{\pi}{6})+9\)
Câu 2:
Áp dụng nguyên hàm từng phần như bài bạn đã đăng:
\(\Rightarrow F(x)=-xe^{-x}-e^{-x}+c\)
Vì \(F(0)=1\Rightarrow -1+c=1\Rightarrow c=2\)
\(\Rightarrow F(x)=-e^{-x}(x+1)+2\), tức B là đáp án đúng
cho hai hàm số y = f(x) = \(a\cdot x^3+b\cdot x^2+c\cdot x+d\)và hàm số y = f(x) =\(a\cdot x^4+b\cdot x^3+c\cdot x^2+d\cdot x+e\). tìm a ,b, c,d, e để y =f(x) là hàm chẵn
cho hàm số y+ f(x) + (m-1)*x (m khác 1.
a. xét công thức đã cho biết đồ thị hàm số đó đi qua điểm A(1;3)
b. tính f(-1); f(-1/2)
c. tìm x để f(x)=-5; f(x)=-4
d. vẽ đồ thị hàm số đã cho
e. trong các điểm B(-2:4) D(-1;-3); e(1/3;1) điểm nào thuộc đò thị đã cho
Cho hàm số \(f\left(x\right)\) có đồ thị \(f'\left(x\right)=\left(e^x-1\right)\left(x^2-x-2\right)\)với mọi \(x\in R\).Số điểm cực tiểu của hàm số đã cho là
A. 0.
B. 1.
C. 2.
D. 3
\(f'\left(x\right)=0\) có 3 nghiệm \(x=-1;0;2\)
Dấu của \(f'\left(x\right)\) trên trục số:
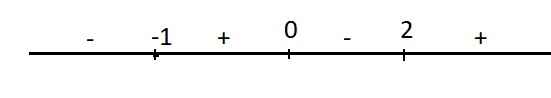
Ta thấy có 2 lần \(f'\left(x\right)\) đổi dấu từ âm sang dương nên hàm có 2 cực tiểu
Tìm số nguyên X, sao cho: a) -7<x<4 b) -2≤x≤9 c)-5<x<0 d) -10≤x≤-4 e) -4<x<-3 f)-2<x≤1
\(a,x\in\left\{-6;-5;...;2;3\right\}\\ b,x\in\left\{-2;-1;...;8;9\right\}\\ c,x\in\left\{-4;-3;-2;-1\right\}\\ d,x\in\left\{-10;-9;...;3;4\right\}\\ e,x\in\varnothing\\ f,x\in\left\{-1;0;1\right\}\)
Cho hai tập hợp E={x∈R, f(x)=0}, F={x∈R, g(x)=0}. Tập hợp H={x∈R, f(x).g(x)=0}. Mệnh đề nào đúng và giải thích:
A. H= E hợp F
B. H= E giao F
C. H= E/F
D. H=F/E
Xét dấu các tam thức bậc hai:
a) f(x)=2x^2 –4x+5 c)f(x)=9x^2 –24x+16 e) f(x)=3x^2 –8x+2
b) f(x)=–x^2 +2x–6 d) f(x)=–4x^2 +4x–1 f)f(x)=–2x^2 +5x–2
Tìm GTLN của biểu thức:
a) A= 5x- x^2
b) B= x- x^2
c) C= 4x- x^2+ 3
d) D= -x^2+ 6x- 11
e) E= 5- 8x- x^2
f) F= 4x- x^2+ 1
I : Tìm giá trị lớn nhất của biểu thức
a) A=5x-x^2 b) B=x-x^2 c) C= 4x-x^2+3
d) D=-x^2+6x-11 e) E=5-8x-x^2 f) F=4x-x^2+1
\(a.A=5x-x^2\)
\(=-\left(x^2-5x\right)=-\left[\left(x-\dfrac{5}{2}\right)^2+\dfrac{25}{4}\right]=-\left(x-\dfrac{5}{2}\right)^2+\dfrac{25}{4}\le\dfrac{25}{4}\)
\(\Rightarrow Max_A=\dfrac{25}{4}\) khi \(x=\dfrac{5}{2}\)
\(b.B=x-x^2=-\left(x^2-x\right)=-\left[\left(x-\dfrac{1}{2}\right)^2-\dfrac{1}{4}\right]=-\left(x-\dfrac{1}{2}\right)^2+\dfrac{1}{4}\le\dfrac{1}{4}\)
\(\Rightarrow Max_B=\dfrac{1}{4}\Leftrightarrow x=\dfrac{1}{2}\)
\(c.C=4x-x^2+3=-\left(x^2-4x-3\right)=-\left(x^2-4x+4-7\right)=-\left(x-2\right)^2+7\le7\)
\(\Rightarrow Max_C=7\Leftrightarrow x=2\)
a) Ta có:
\(A=5x-x^2\)
\(=-\left(x^2-5x\right)\)
\(=-\left(x^2-5x\right)-6,25+6,25\)
\(=-\left(x^2-5x+6,25\right)+6,25\)
\(=-\left(x-2,5\right)^2+6,25\)
Ta lại có:
\(\left(x-2,5\right)^2\ge0\)
\(\Rightarrow-\left(x-2,5\right)^2\le0\)
\(\Rightarrow-\left(x-2,5\right)^2+6,25\le6,25\)
\(\Rightarrow A\le6,25\)
Dấu "=" xảy ra \(\Leftrightarrow\left(x-2,5\right)^2=0\)
\(\Leftrightarrow x-2,5=0\)
\(\Leftrightarrow x=2,5\)
Vậy MaxA = 6,25 \(\Leftrightarrow x=2,5\)
\(d.D=-x^2+6x-11=-\left(x^2-6x+11\right)=-\left(x-3\right)^2-2\le-2\)
\(\Rightarrow Max_D=-2\Leftrightarrow x=3\)
\(e.E=5-8x-x^2=-\left(x^2+8x-5\right)=-\left[\left(x+4\right)^2-21\right]=-\left(x+4\right)^2+21\le21\)
\(\Rightarrow Max_E=21\Leftrightarrow x=-4\)
\(f.F=4x-x^2+1=-\left(x-4x-1\right)=-\left[\left(x-2\right)^2-5\right]=-\left(x-2\right)^2+5\le5\)
\(\Rightarrow Max_F=5\Leftrightarrow x=2\)