Các câu hỏi tương tự
Cho hàm số \(y=f\left(x\right)\)không âm có đạo hàm trên \(\left[0;\frac{\pi}{4}\right]\)thỏa mãn \(f\left(x\right)=\frac{f'\left(x\right)}{cosx}\).Biết \(f\left(0\right)=1\).giá trị của \(f\left(\frac{\pi}{4}\right)?\)(Đáp án:\(e^{\frac{\sqrt{2}}{2}}\))
Cho hàm số y f(x) có đạo hàm liên tục trên khoảng thỏa mãn
x
2
f
x
+
f
x
0
và
f
x
≠
0
,
∀...
Đọc tiếp
Cho hàm số y= f(x) có đạo hàm liên tục trên khoảng ![]() thỏa mãn
x
2
f
'
x
+
f
x
=
0
và
f
x
≠
0
,
∀
x
∈
0
;
+
∞
. Tính f(2) biết f(1) = e.
thỏa mãn
x
2
f
'
x
+
f
x
=
0
và
f
x
≠
0
,
∀
x
∈
0
;
+
∞
. Tính f(2) biết f(1) = e.
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Cho hàm số y f(x) có đạo hàm f’(x) liên tục trên đoạn [0; 1] thỏa mãn f(1) 1 và
I
∫
0
1
f
x
d
x
2
. Tính tích phân
I
∫
0
1
f
x
d
x
A. I -1. B. I 1. C. I 2. D. I -2.
Đọc tiếp
Cho hàm số y = f(x) có đạo hàm f’(x) liên tục trên đoạn [0; 1] thỏa mãn f(1) = 1 và I = ∫ 0 1 f x d x = 2 . Tính tích phân I = ∫ 0 1 f ' x d x
A. I = -1.
B. I = 1.
C. I = 2.
D. I = -2.
Cho hàm số f(x) có đạo hàm f(x) liên tục trên đoạn [1;e] thỏa mãn
f
1
1
2
và
x
.
f
x
xf
2
x
-
3...
Đọc tiếp
Cho hàm số f(x) có đạo hàm f'(x) liên tục trên đoạn [1;e] thỏa mãn f 1 = 1 2 và x . f ' x = xf 2 x - 3 f x + 1 x , ∀ x ∈ 1 ; e . Giá trị của f(e) bằng
A. ![]() .
.
B. ![]() .
.
C. ![]() .
.
D. ![]() .
.
Cho hàm số yf(x) thỏa mãn
f
(
x
)
+
2
x
f
(
x
)
e
-
x
2
,
∀
x
∈
R
và f(1)0 Tính giá trị f(2).
Đọc tiếp
Cho hàm số y=f(x) thỏa mãn f ' ( x ) + 2 x f ( x ) = e - x 2 , ∀ x ∈ R và f(1)=0 Tính giá trị f(2).
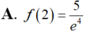
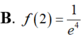
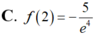
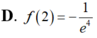
Cho hàm số \(f\left(x\right)\) có đạo hàm bằng \(f'\left(x\right)=x^2\left(x-1\right)^3\left(x-2\right)\) . Số điểm cực trị của hàm số \(f\left(x\right)\) bằng:
A.0 B.1 C.2 D.3
Cho hàm số y=f(x) xác định và liên tục trên R thõa mãn các điều kiện sau:
\(\hept{\begin{cases}f\left(x\right)>0,\forall x\in R\\f'\left(x\right)=-e^xf^2\left(x\right),\forall x\in R\\f\left(o\right)=\frac{1}{2}\end{cases}}\)
Hãy tính \(f\left(ln2\right)\).
Cho hàm số f(x) có đạo hàm không âm trên [0;1] thỏa mãn
[
f
(
x
)
]
4
.
[
f
(
x
)
]
2
(
x
2
+
1
)
1...
Đọc tiếp
Cho hàm số f(x) có đạo hàm không âm trên [0;1] thỏa mãn [ f ( x ) ] 4 . [ f ' ( x ) ] 2 ( x 2 + 1 ) = 1 + f 3 ( x ) và f(x)>0 biết f(0) = 2 Hãy chọn khẳng định đúng trong các khẳng định sau:
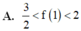
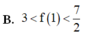
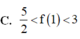
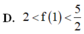
Cho hàm số f(x) có đạo hàm liên tục trên đoạn [0;1] thỏa mãn f(0)1 và
∫
0
1
[
f
(
x
)
]
2
d
x
∫
0
1
(
x
+
1
)
e
x...
Đọc tiếp
Cho hàm số f(x) có đạo hàm liên tục trên đoạn [0;1] thỏa mãn f(0)=1 và
∫ 0 1 [ f ' ( x ) ] 2 d x = ∫ 0 1 ( x + 1 ) e x d x = e 2 - 1 4
Tính tích phân I = ∫ 0 1 f ( x ) d x
A. I = 2 - e
B. e - 2
C. I = e/2
D. I = (e-1)/2








