Cho hàm số y = sinx − cosx + 1 sinx + cosx − 2 . Giả sử hàm số có giá trị lớn nhất là M, giá trị nhỏ nhất là m. Khi đó giá trị của M+m là
A. 1
B. 4
C. 2
D. 0
Cho hàm số: y = ex cosx Khi đó: y'/ex?
A. cosx - sinx
B. sinx - cosx
C. sinx + cosx
D. cosx
\(y'=\left(e^x\right)'.cosx+e^x.\left(cosx\right)'=e^x\left(cosx-sinx\right)\)
=> Chọn A
Cho hàm số y = 1 + sin x 1 + cos x . Xét hai kết quả:
(I) y ' = ( cos x - sin x ) ( 1 + cos x + sin x ) 1 + cos x 2
(II) y ' = 1 + cos x + sin x 1 + cos x 2
Kết quả nào đúng?
A. Cả hai đều sai.
B. Chỉ (II).
C. Chỉ (I).
D. Cả hai đều đúng.
- Ta có :
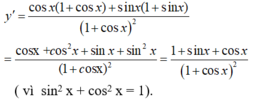
+) Xét (I) ta có:
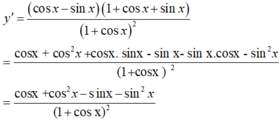
+) Do đó, (I) đúng và (II) sai.
Chọn B.
Cho hàm số y = 1 + sin x 1 + cos x . Xét hai kết quả:
(I) y ' = ( cos x - sin x ) ( 1 + cos x + sin x ) 1 + cos x 2
(II) y ' = 1 + cos x + sin x 1 + cos x 2
Kết quả nào đúng?
A. Cả hai đều sai.
B. Chỉ (II).
C. Chỉ (I).
D. Cả hai đều đúng.
- Ta có :
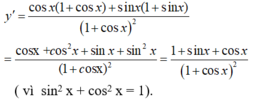
+) Xét (I) ta có:
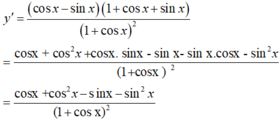
+) Do đó, (I) đúng và (II) sai.
Chọn B.
1, Tìm txd của hàm số sau
a, y = \(\sqrt{sinx-1}\)
b, y =\(\sqrt{\dfrac{1-sinx}{1+sinx}}\)
c, y = \(\dfrac{1+cosx}{sinx}\)
ĐKXĐ: (tất cả \(k\in Z\))
a. \(sinx-1\ge0\Leftrightarrow sinx\ge1\)
\(\Leftrightarrow sinx=1\Rightarrow x=\dfrac{\pi}{2}+k2\pi\)
b. \(\left\{{}\begin{matrix}\dfrac{1-sinx}{1+sinx}\ge0\left(luôn-đúng\right)\\1+sinx\ne0\end{matrix}\right.\) \(\Leftrightarrow sinx\ne-1\)
\(\Leftrightarrow x\ne-\dfrac{\pi}{2}+k2\pi\)
c. \(sinx\ne0\Leftrightarrow x\ne k\pi\)
Tìm tập xác định của các hàm số sau:
1,\(y=sin\dfrac{3x+2}{2x-1}\)
2,\(y=tan\left(3x+\dfrac{2\pi}{5}\right)\)
3,\(y=cot\left(2x-\dfrac{1}{3}\right)\)
4,\(y=\dfrac{sinx+cosx}{sinx-cosx}\)
5,\(y=\dfrac{1}{sinx}+\dfrac{1}{cosx}\)
6,\(y=\dfrac{\sqrt{1-sinx}}{cosx}\)
7,\(y=\dfrac{3}{sin^2x-cos^2x}\)
8,\(y=\dfrac{1+tanx}{1+sinx}\)
9,\(y=\sqrt{\dfrac{1+sinx}{1-cosx}}\)
Đạo hàm của hàm số : y = \(\dfrac{sinx}{sinx-cosx}\) là
tìm tập xác định của hàm số
a. y=\(\dfrac{sinx}{cosx-1}\)
b.y=\(\sqrt{sinx-1}\)
c.y=\(\sqrt{\dfrac{1+sinx}{1-cosx}}\)
a: ĐKXĐ: \(cosx-1\ne0\)
=>\(cosx\ne1\)
=>\(x\ne k2\Omega\)
b: ĐKXĐ: sin x-1>=0
=>sin x>=1
mà \(-1< =sinx< =1\)
nên sin x=1
=>\(x=\dfrac{\Omega}{2}+k2\Omega\)
c:
-1<=sin x<=1
=>-1+1<=sin x+1<=1+1
=>0<=sin x+1<=2
ĐKXĐ: \(\dfrac{1+sinx}{1-cosx}>=0\)
mà \(1+sinx>=0\)(cmt)
nên \(1-cosx>0\)
=>\(cosx< 1\)
mà -1<=cosx<=1
nên \(cosx\ne1\)
=>\(x\ne k2\Omega\)
Cho hàm số f ( x ) = 1 + cos x k h i sin x ⩾ 0 3 - cos x k h i sin x < 0 . Hàm số có bao nhiêu điểm gián đoạn trên khoảng (0;2019)?
A.Vô số
B.320
C.321
D.319
Tìm TXĐ của hàm số \(y=\dfrac{sinx}{\sqrt{3}sinx+cosx}\)
\(\sqrt{3}sinx+cosx\ne0\)
\(\Leftrightarrow\dfrac{\sqrt{3}}{2}sinx+\dfrac{1}{2}cosx\ne0\)
\(\Leftrightarrow sin\left(x+\dfrac{\pi}{6}\right)\ne0\)
\(\Leftrightarrow x+\dfrac{\pi}{6}\ne k\pi\)
\(\Leftrightarrow x\ne-\dfrac{\pi}{6}+k\pi\)
Hàm số y = (1+sinx)(1+cosx) có đạo hàm là:
A. y'=cosx -sinx +1
B. y'=cosx +sinx +cos2x
C. y'=cosx -sinx +cos2x
D. y'=cosx +sinx +1