Cho phương trình tan x + tan x + π 4 = 1. Diện tích của đa giác tạo bởi các điểm trên đường tròn lượng giác biểu diễn các họ nghiệm của phương trình gần với số nào nhất trong các số dưới đây?
A. 0,948
B. 0,949
C. 0,946
D. 0,947
Giải phương trình sau: tanx + tan (x+π/4) = 1
Điều kiện:
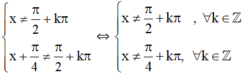
⇔ tan x.(1 - tanx) + tanx + 1 = 1 – tan x.
⇔ tan x - tan2x + 2.tan x = 0
⇔ tan2x - 3tanx = 0
⇔ tanx(tanx - 3) = 0
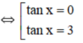
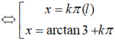
Vậy phương trình đã cho có tập nghiệm là:
{arctan 3+kπ; k ∈ Z }
Giải phương trình: Tan(x-π/4) = Tan2x
\(\Leftrightarrow2x=x-\dfrac{\pi}{4}+k\pi\)
\(\Leftrightarrow x=-\dfrac{\pi}{4}+k\pi\) (\(k\in Z\))
Phương trình tan( x - π/4) = 0 có nghiệm là:
A. x = π/4 + kπ, k ∈ Z.
B. x = 3π/4 + kπ, k ∈ Z.
C. x = kπ, k ∈ Z.
D. x = k2π, k ∈ Z.
Số nghiệm thuộc khoảng ( 0 ; π ) của phương trình. tan x + sin x + tan x - sin x = 3 tan x là
A. 0
B. 1
C. 2
D. 3
Phương trình tan ( x + π/ 3) có nghiệm là:
![]()
![]()
![]()
![]()
a) Giải phương trình \(\tan x = 1\)
b) Tìm góc lượng giác x saoo cho \(\tan x = \tan {67^ \circ }\)
a) \(\tan x = 1 \Leftrightarrow \tan x = \tan \frac{\pi }{4} \Leftrightarrow x = \frac{\pi }{4} + k\pi \)
b) \(\tan x = \tan {67^ \circ } \Leftrightarrow x = {67^ \circ } + k{.180^ \circ }\)
Sin(x-π/2)+cos(x-π)+tan(5π/2-x)+tan(x-π/2)=-2cosx
\(sin\left(x-\dfrac{\pi}{2}\right)+cos\left(x-\pi\right)+tan\left(\dfrac{5\pi}{2}-x\right)+tan\left(x-\dfrac{\pi}{2}\right)\)
\(=-sin\left(\dfrac{\pi}{2}-x\right)+cos\left(\pi-x\right)+tan\left(2\pi+\dfrac{\pi}{2}-x\right)-tan\left(\dfrac{\pi}{2}-x\right)\)
\(=-cosx-cosx+tan\left(\dfrac{\pi}{2}-x\right)-cotx\)
\(=-2cosx+cotx-cotx=-2cosx\)
Mấy bạnn giải chii tiết raa giúp mik với nhaa Câu 1: nghiệm dương nhỏ nhất của pt tan x=tan (6π/5) A. x=π/5 B. x=6π/5 C. x=6/5 D. x=6π Câu 2: tìm nghiệm thuộc đoạn [0;π] của pt cot 2x=cot(π/2-x) A. 2 B. 3 C.1 D.4 Câu 3: tìm tổng các nghiệm thuộc khoảng (-π/2;π/2) của pt 4sin²2x-1=0 A.0 B. π/6 C. π/3 D. π Câu 4: tìm tổng các nghiệm của pt cos(x+π/4)=1/2 trong khoảng (-π;π) A. π/2 B. -π/2 C. -3π/2 D. π/4
Giải các phương trình sau :
a) \(\tan\left(2x+1\right)\tan\left(3x-1\right)=1\)
b) \(\tan x+\tan\left(x+\dfrac{\pi}{4}\right)=1\)
a) tan(2x + 1)tan(3x - 1) = 1 ⇔ = 1.
Với điều kiện cos(2x + 1)cos(3x - 1) ≠ 0 phương trình tương đương với
cos(2x + 1)cos(3x - 1) - sin(2x + 1)sin(3x - 1) = 0
⇔ cos(2x + 1 + 3x - 1) = 0 ⇔ 5x = + k π ⇔ x =
+
, k ∈ Z.
Cần chọn các k nguyên để x = +
không thỏa mãn điều kiện của phương trình (để loại bỏ). Điều này chỉ xảy ra trong các trường hợp sau:
(i) x = +
làm cho cos(2x + 1) = 0, tức là
cos[2( +
) + 1] = 0 ⇔
+ 1 =
+ lπ, (l ∈ Z)
⇔ π( -
) = 1 ⇔ π =
, suy ra π ∈ Q, vô lí.
Vì vậy không có k nguyên nào để x = +
làm cho cos(2x + 1) = 0.
(ii) x = +
làm cho cos(3x - 1) = 0. Tương tự (i),ta cũng thấy không có k nguyên nào để x =
+
làm cho cos(3x - 1) = 0.
Vậy ∀ k ∈ Z, x = +
đều là nghiệm của phương trình đã cho.
b)Đặt t = tan x, phương trình trở thành
t + = 1 ⇔ -t2 + 3t = 0 (điều kiện t ≠ 1) ⇔ t = 0 hoặc t = 3 (thỏa mãn)
Vậy tan x = 0 ⇔ x = kπ
tan x = 3 ⇔ x = arctan 3 + kπ (k ∈ Z)
Giải các Phương trình sau
a) \(sin^4\frac{x}{2}+cos^4\frac{x}{2}=\frac{1}{2}\)
b) \(sin^6x+cos^6x=\frac{7}{16}\)
c) \(sin^6x+cos^6x=cos^22x+\frac{1}{4}\)
d) \(tanx=1-cos2x\)
e) \(tan(2x+\frac\pi3).tan(\frac\pi3-x)=1\)
f) \(tan(x-15^o).cot(x+15^o)=\frac{1}{3}\)
a.
\(\left(sin^2\dfrac{x}{2}+cos^2\dfrac{x}{2}\right)^2-2sin^2\dfrac{x}{2}cos^2\dfrac{x}{2}=\dfrac{1}{2}\)
\(\Leftrightarrow2-\left(2sin\dfrac{x}{2}cos\dfrac{x}{2}\right)^2=1\)
\(\Leftrightarrow1-sin^2x=0\)
\(\Leftrightarrow cos^2x=0\)
\(\Leftrightarrow x=\dfrac{\pi}{2}+k\pi\)
b.
\(\left(sin^2x+cos^2x\right)^3-3sin^2x.cos^2x\left(sin^2x+cos^2x\right)=\dfrac{7}{16}\)
\(\Leftrightarrow1-\dfrac{3}{4}\left(2sinx.cosx\right)^2=\dfrac{7}{16}\)
\(\Leftrightarrow16-12.sin^22x=7\)
\(\Leftrightarrow3-4sin^22x=0\)
\(\Leftrightarrow3-2\left(1-cos4x\right)=0\)
\(\Leftrightarrow cos4x=-\dfrac{1}{2}\)
\(\Leftrightarrow4x=\pm\dfrac{2\pi}{3}+k2\pi\)
\(\Leftrightarrow x=\pm\dfrac{\pi}{6}+\dfrac{k\pi}{2}\)
c.
\(\left(sin^2x+cos^2x\right)^3-3sin^2x.cos^2x\left(sin^2x+cos^2x\right)=cos^22x+\dfrac{1}{4}\)
\(\Leftrightarrow1-\dfrac{3}{4}\left(2sinx.cosx\right)^2=cos^22x+\dfrac{1}{4}\)
\(\Leftrightarrow3-3sin^22x=4cos^22x\)
\(\Leftrightarrow3=3\left(sin^22x+cos^22x\right)+cos^22x\)
\(\Leftrightarrow3=3+cos^22x\)
\(\Leftrightarrow cos2x=0\)
\(\Leftrightarrow x=\dfrac{\pi}{4}+\dfrac{k\pi}{2}\)