Cho hàm số y = cos 2 2 x . Kết quả của biểu thức y ' ' ' + y ' ' + 16 y ' + 16 y - 8 là:
A. 0
B. 8
C. -8
D. 16
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Những câu hỏi liên quan
Cho biểu thức \(B=cos^2x+cos^2\left(x+y\right)-2cosx.cosy.cos\left(x+y\right)\). Rút gọn B ta được kết quả \(B=a+bcos2y\). Tính giá trị \(H=2a+3b\)
\(B=cos^2x+cos^2\left(x+y\right)-\left[cos\left(x+y\right)+cos\left(x-y\right)\right]cos\left(x+y\right)\)
\(=cos^2x+cos^2\left(x+y\right)-cos^2\left(x+y\right)-cos\left(x-y\right)cos\left(x+y\right)\)
\(=cos^2x-\dfrac{1}{2}\left(cos2x+cos2y\right)\)
\(=\dfrac{1}{2}+\dfrac{1}{2}cos2x-\dfrac{1}{2}cos2x-\dfrac{1}{2}cos2y\)
\(=\dfrac{1}{2}-\dfrac{1}{2}cos2y\Rightarrow\left\{{}\begin{matrix}a=\dfrac{1}{2}\\b=-\dfrac{1}{2}\end{matrix}\right.\)
Đúng 1
Bình luận (0)
Cho hàm số y = c o s 2 2 x . Kết quả của biểu thức y ' ' ' + y ' ' + 16 y ' + 16 y − 8 là:
A. 0
B. 8
C. -8
D. 16
Câu 1:
Biết x+y=1 và x^2 + y^2 =25 . Giá trị của xy là ....
Câu 2:
Cho hàm số y=f(x)=2x-7.Với x=3 thì y=?
Câu 10:
Rút gọn biểu thức (a^2+b^2)^2 - 4a^2.b^2 với a^2 - b^2 ta được kết quả ....
Câu 1: x^2 + y^2 = 25
=> x^2 + y^2 +2xy - 2xy = 25
=> \(\left(x+y\right)^2\)\(-2xy=25\)
=> \(1-2xy=25\)=> \(-2xy=-24\) => xy = 12
Câu 10: (a^2 + b^2)^2 - 4a^2.b^2 = a^4 +2a^2.b^2 + b^2 - 4a^2.b^2 = a^4 - 2a^2.b^2 + b^2 = (a^2 - b^2)^2
Đúng 0
Bình luận (0)
Quan sát đồ thị y cos x ở Hình 28a) Nêu tập giá trị của hàm số y cos xb) Trục tung có là trục đối xứng của đồ thị hàm số không? Từ đó kết luận tính chẵn, lẻ của hàm số y cos xc) Bằng cách dịch chuyển đồ thị y cos x trên đoạn left[ { - pi ;pi } right] song song với trục hoành sang phải theo đoạn có độ dài 2pi , ta nhận được đồ thị có hàm số y cos x trên đoạn left[ {pi ;3pi } right] hay không? Hàm số y cos x có tuần hoàn hay không?d) Tìm khoảng đồng biến, nghịch biến của hàm...
Đọc tiếp
Quan sát đồ thị \(y = \cos x\) ở Hình 28
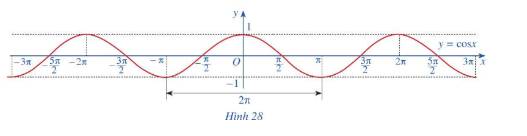
a) Nêu tập giá trị của hàm số \(y = \cos x\)
b) Trục tung có là trục đối xứng của đồ thị hàm số không? Từ đó kết luận tính chẵn, lẻ của hàm số \(y = \cos x\)
c) Bằng cách dịch chuyển đồ thị \(y = \cos x\) trên đoạn \(\left[ { - \pi ;\pi } \right]\) song song với trục hoành sang phải theo đoạn có độ dài \(2\pi \), ta nhận được đồ thị có hàm số \(y = \cos x\) trên đoạn \(\left[ {\pi ;3\pi } \right]\) hay không? Hàm số \(y = \cos x\) có tuần hoàn hay không?
d) Tìm khoảng đồng biến, nghịch biến của hàm số \(y = \cos x\)
a) Tập giá trị của hàm số \(y = \cos x\)là \(\left[ { - 1;1} \right]\)
b) Trục tung là trục đối xứng của hàm số \(y = \cos x\).
Như vậy hàm số \(y = \cos x\)là hàm số chẵn.
c) Bằng cách dịch chuyển đồ thị \(y = \cos x\) trên đoạn \(\left[ { - \pi ;\pi } \right]\) song song với trục hoành sang phải theo đoạn có độ dài \(2\pi \), ta nhận được đồ thị có hàm số \(y = \cos x\) trên đoạn \(\left[ {\pi ;3\pi } \right]\)
Như vậy hàm số \(y = \cos x\) là hàm số tuần hoàn
d) Hàm số \(y = \cos x\)đồng biến trên mỗi khoảng \(\left( { - \pi + k2\pi ;k2\pi } \right)\), nghịch biến trên mỗi khoảng \(\left( {k2\pi ;\pi + k2\pi } \right)\) với \(k \in Z\)
Đúng 0
Bình luận (0)
Gọi M và N lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số
y
-
1
+
2
.
cos
x
2
-
3
.
sin
x...
Đọc tiếp
Gọi M và N lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của hàm số y = - 1 + 2 . cos x 2 - 3 . sin x + cos x trên ℝ . Biểu thức M + N + 2 có giá trị bằng:
A. 0
B. 4 2 - 3
C. 2
D . 2 + 3 + 2
Hàm số y=cos x. sin2x có đạo hàm là biểu thức nào sau đây
Cho các công thức: y=x +3 , y= -2x ; y mũ 2 = x.Có bao nhiêu công thức biểu diễn y là hàm số của x?
SGK Kết nối tri thức và cuộc sống
17 tháng 8 2023 lúc 10:39
Bằng cách viết \(y = \cos x = \sin \left( {\frac{\pi }{2} - x} \right),\) tính đạo hàm của hàm số \(y = \cos x.\)
\(y'=\left(cosx\right)'\\ =\left(\dfrac{\pi}{2}-x\right)'cos\left(\dfrac{\pi}{2}-x\right)\\ =-cos\left(\dfrac{\pi}{2}-x\right)\\ =-sinx\)
Đúng 0
Bình luận (0)
18 tháng 12 2021 lúc 21:05
Cho x và y là hai đại lượng tỉ lệ nghịch. Biết nếu x = 16 thì y = 12. Nếu x = 4 thì y bằng …… *
Kết quả rút gọn biểu thức *
\(=\left(\dfrac{39}{4}:\dfrac{26}{5}+\dfrac{17}{5}\cdot\dfrac{55}{24}\right):\dfrac{-25}{16}\)
=-464/75
Đúng 2
Bình luận (0)