Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Các câu hỏi tương tự
Xét sự đồng biến, nghịch biến của các hàm số:a) y 3
x
2
− 8
x
3
b) y 16x + 2
x
2
− 16
x
3
/3 −
x
4
c) y
x
3
− 6
x
2
+ 9xd) y
x
4
+ 8...
Đọc tiếp
Xét sự đồng biến, nghịch biến của các hàm số:
a) y = 3 x 2 − 8 x 3
b) y = 16x + 2 x 2 − 16 x 3 /3 − x 4
c) y = x 3 − 6 x 2 + 9x
d) y = x 4 + 8 x 2 + 5
Gọi (H) là hình phẳng giới hạn bởi parabol (P)
y
8
x
-
x
2
và trục hoành. Các đường thẳng y a; y b;y c với 0abc16 chia (H) thành bốn phần có diện tích bằng nhau. Giá trị của biểu thức
16
-
a
3
+
16
-
b...
Đọc tiếp
Gọi (H) là hình phẳng giới hạn bởi parabol (P) y = 8 x - x 2 và trục hoành. Các đường thẳng y = a; y = b;y =c với 0<a<b<c<16 chia (H) thành bốn phần có diện tích bằng nhau. Giá trị của biểu thức 16 - a 3 + 16 - b 3 + 16 - c 3 bằng
A. 2048.
B. 3584.
C. 2816.
D. 3480.
cho hàm số y=X4-2mx2+m(C) với m là tham số thực.Gọi A là điểm thuộc đồ thị (C) có hoành độ bằng 1.tìm tham số m để tiếp tuyến đenta với đồ thị (C) tại A cắt đường tròn (T): x2+(y-1)2=4 tạo thành dây cung có độ dài nhỏ nhất
A.m=16/13
B.-13/16
C.13/16
D.-16/13
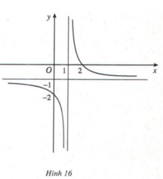
Cho hàm số y = (2 - x)/(x - 1) (H.16) có đồ thị (C).
Nêu nhận xét về khoảng cách từ điểm M(x; y) ∈ (C) tới đường thẳng y = -1 khi |x| → +∞
Cho hai số dương x, y thỏa mãn
l
o
g
2
(
4
x
+
y
+
2
x
y
+
2
)
y
+
2
8
-
2
x
-
2
y
+
2...
Đọc tiếp
Cho hai số dương x, y thỏa mãn l o g 2 ( 4 x + y + 2 x y + 2 ) y + 2 = 8 - 2 x - 2 y + 2 . Giá trị nhỏ nhất của P = 2 x + y là số có dạng M = a b + c với a , b ∈ ℕ , a > 2 . Tính S = a + b + c
A. 17
B. 7
C. 19
D. 3
Biểu thức tổng quát của hàm số có đò thị như hình 1.6 là:A. y a
x
2
+ bx + c với a ≠ 0B. y a
x
3
+ cx + d với a 0C. y a
x
3
+ b
x
2
+ cx + d với a 0 và
b
2
- 3ac 0D. y
x
3
Đọc tiếp
Biểu thức tổng quát của hàm số có đò thị như hình 1.6 là:
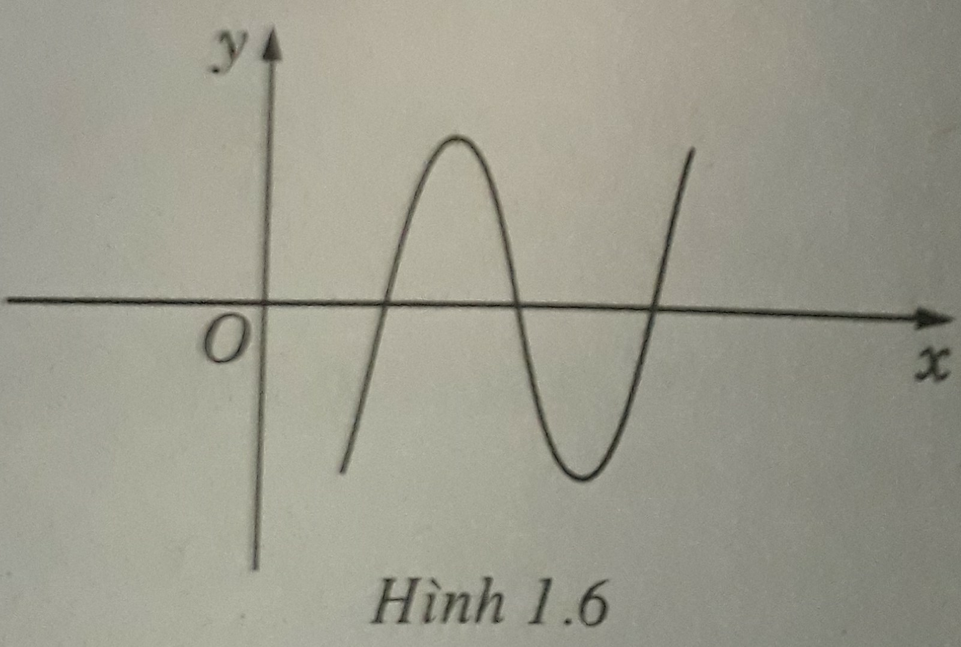
A. y = a x 2 + bx + c với a ≠ 0
B. y = a x 3 + cx + d với a < 0
C. y = a x 3 + b x 2 + cx + d với a > 0 và b 2 - 3ac > 0
D. y = x 3
Biểu thức tổng quát của hàm số có đồ thị như hình 1.6 là:A. y a
x
2
+ bx + c với a
≠
0B. y a
x
3
+ cx + d với a 0C. y a
x
3
+ b
x
2
+ cx + d với a 0 và
b
2
- 3ac 0D. y ...
Đọc tiếp
Biểu thức tổng quát của hàm số có đồ thị như hình 1.6 là:
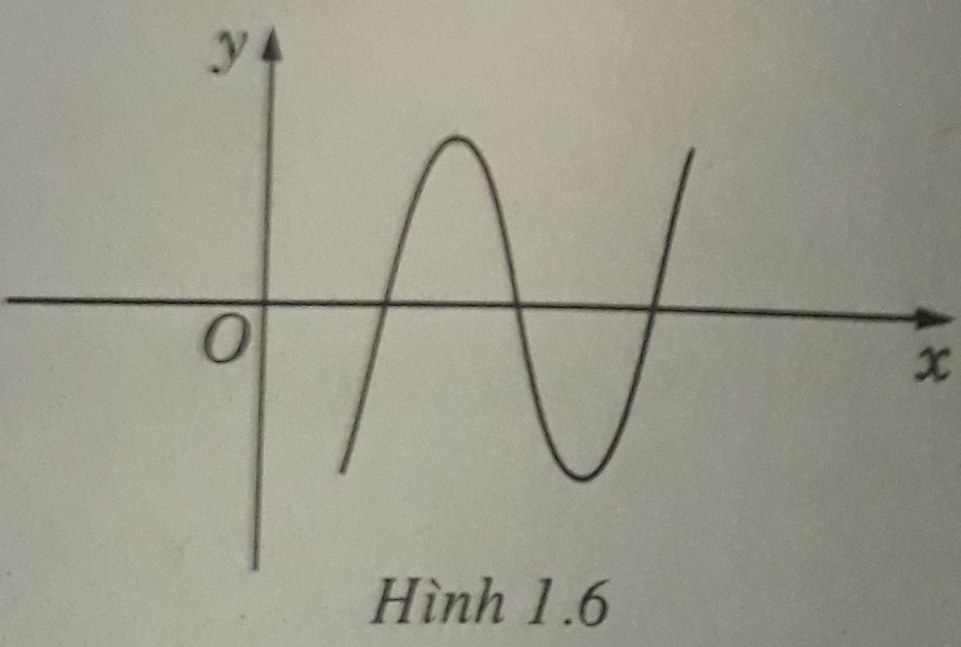
A. y = a x 2 + bx + c với a ≠ 0
B. y = a x 3 + cx + d với a < 0
C. y = a x 3 + b x 2 + cx + d với a > 0 và b 2 - 3ac > 0
D. y = x 3
Cho
S
:
x
-
1
2
+
y
+
1
2
+
z
-
3
3
16
và
P
:
2
x...
Đọc tiếp
Cho S : x - 1 2 + y + 1 2 + z - 3 3 = 16 và P : 2 x - y + 2 z = 0 . Biết (S) cắt (P) theo giao tuyến là đường tròn (C). Tính bán kính r của (C).
![]()
![]()
![]()
![]()
Tiệm cận đứng và ngang của đồ thị hàm số sau là:
y = - 3 x - 2
A. x = 2, y = 0 B. x = 0, y = 2
C. x = 1, x = 1 D. x = -2; y = -3





