\(P=\left(a+b+c\right)+\left(a+\frac{4}{a}\right)+\left(3b+\frac{12}{b}\right)+\left(5c+\frac{20}{c}\right)\)

Theo BĐT AM-GM và gt ta có: \(P\ge6+4+12+20=42\).

Đẳng thức xảy ra khi \(a=b=c=2\)

Vậy \(minP=42\)

Chọn đáp án B.

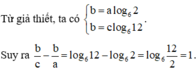
DISCOVERY

Một cách tổng quát chúng ta có các kết quả sau:

1) Cho các số thực dương m, n, p khác 1 và thỏa mãn m.p =  n α

Nếu tồn tại các số thực a, b, c thỏa mãn hệ thức 

2) Cho các số thực dương m, n, p khác 1 và thỏa mãn 

 Nếu tồn tại các số thực a, b, c thỏa mãn hệ thức 

Ta có:

\(9=\left(b\sqrt{a}+b\sqrt{b}+a\sqrt{c}\right)^2\le\left(a^2+b^2+c^2\right)\left(a+b+c\right)\le\left(a^2+b^2+c^2\right)\sqrt{3\left(a^2+b^2+c^2\right)}\)

\(\Leftrightarrow81\le3\left(a^2+b^2+c^2\right)^3\Leftrightarrow27\le\left(a^2+b^2+c^2\right)^3\)

\(\Leftrightarrow3\le a^2+b^2+c^2\Rightarrow\dfrac{9}{a^2+b^2+c^2}\le\dfrac{9}{3}=3\)

Dấu "=" xảy ra khi a=b=c=1

c1:áp dụng bđt AM-GM:

\(a+b\ge2\sqrt{ab}\Rightarrow ab\le\left(\dfrac{a+b}{2}\right)^2=1008^2\)

=> đáp án A

c2: tương tự c1 . đáp án b

3.

\(\dfrac{a}{b}+\dfrac{b}{a}\ge2\sqrt{\dfrac{ab}{ab}}=2\)

Đáp án A

4.

\(a^2-a+1=\left(a-\dfrac{1}{2}\right)^2+\dfrac{3}{4}>0\) ;\(\forall a\)

Đáp án A

Ta có \(12=a+b+2ab\le a+b+\dfrac{\left(a+b\right)^2}{2}\Leftrightarrow\left(a+b\right)^2+2\left(a+b\right)-24\ge0\Leftrightarrow\left(a+b+6\right)\left(a+b-4\right)\ge0\Leftrightarrow a+b\ge4\) (Do a + b + 6 > 0)

Dấu "=" xảy ra khi a = b = 2.

bạn kiểm tra lại xem có sai đề không

\(P=\dfrac{ab}{a+b}+\dfrac{bc}{b+c}+\dfrac{ca}{c+a}\)

\(P\le\dfrac{ab}{4}\left(\dfrac{1}{a}+\dfrac{1}{b}\right)+\dfrac{bc}{4}\left(\dfrac{1}{b}+\dfrac{1}{c}\right)+\dfrac{ca}{4}\left(\dfrac{1}{c}+\dfrac{1}{a}\right)\)

\(\Leftrightarrow P\le\dfrac{1}{2}\left(a+b+c\right)=3\)

\(P_{max}=3\) khi \(a=b=c\)