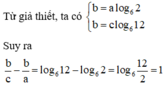Các câu hỏi tương tự
Cho các số dương a, b, c thỏa mãn
2
a
6
b
12
c
. Khi đó biểu thức
T
b
c
-
b
a
có giá trị là A.
3
2
B. 1 C. 2 D.
1
2
Đọc tiếp
Cho các số dương a, b, c thỏa mãn 2 a = 6 b = 12 c . Khi đó biểu thức T = b c - b a có giá trị là
A. 3 2
B. 1
C. 2
D. 1 2
Cho a,b,c là các số thực dương thỏa mãn
a
log
5
2
4
,
b
log
4
6
1
,
log
,
c
log
7
3
49
Tính giá trị của biểu thức
T
a...
Đọc tiếp
Cho a,b,c là các số thực dương thỏa mãn a log 5 2 = 4 , b log 4 6 = 1 , log , c log 7 3 = 49 Tính giá trị của biểu thức T = a log 2 2 5 + b log 4 2 6 + 3 c log 7 2 3
A. T=126
B. T = 5 + 2 3
C. T=88
D. T = 3 - 2 3
Cho các số thực a;b;c;d thay đổi, luôn thỏa mãn
a
-
1
2
+
b
-
2
2
1
và
4
c
-
3
d
-
23
0
. Giá trị nhỏ nhất của biểu thức
P
:...
Đọc tiếp
Cho các số thực a;b;c;d thay đổi, luôn thỏa mãn a - 1 2 + b - 2 2 = 1 và 4 c - 3 d - 23 = 0 . Giá trị nhỏ nhất của biểu thức P : a - c 2 + b - d 2 là:
A. P m i n = 28
B. P m i n = 3
C. P m i n = 4
D. P m i n = 16
Cho hai số thực không âm x,y ≤ 1. Biết
P
l
n
(
1
+
x
2
)
(
1
+
y
2
)
+
8
17
(
x
+
y
)
2
có giá trị nhỏ nhất là
-
a
b
+
2
ln
c...
Đọc tiếp
Cho hai số thực không âm x,y ≤ 1. Biết P = l n ( 1 + x 2 ) ( 1 + y 2 ) + 8 17 ( x + y ) 2 có giá trị nhỏ nhất là - a b + 2 ln c d trong đó a, b, c, d là số tự nhiên thỏa mãn ước chung của (a,b) = (c,d) = 1. Giá trị của a+b+c+d là
A. 406
B. 56
C. 39
D. 405
Cho a, b, c là các số thực dương khác 1 và thỏa mãn
a
log
3
7
27
,
b
l
o
g
7
11
49
,
c
log
11
25
11
.
Tính giá trị của biểu t...
Đọc tiếp
Cho a, b, c là các số thực dương khác 1 và thỏa mãn a log 3 7 = 27 , b l o g 7 11 = 49 , c log 11 25 = 11 . Tính giá trị của biểu thức T = a log 3 2 7 + b l o g 7 2 11 + c log 11 2 25
A. T=469
B. T=3141
C. T=2017
D. T = 76 + 11
Cho phương trình
4
-
x
-
a
.
log
3
x
2
-
2
x
+
3
+
2
-
x...
Đọc tiếp
Cho phương trình 4 - x - a . log 3 x 2 - 2 x + 3 + 2 - x 2 + 2 x . log 1 3 2 x - a + 2 = 0 . Tập tất cả các giá trị của tham số a để phương trình có 4 nghiệm x 1 ; x 2 ; x 3 ; x 4 thỏa mãn là (c;d). Khi đó giá trị biểu thức T = 2 c + 2 d bằng:
A. 5
B. 2
C. 3
D. 4
Cho hàm số f(x) xác định trên
(
-
∞
;
-
1
)
∪
(
0
;
+
∞
)
thỏa mãn
f
(
x
)
1
x
2
+
x
,
f
(
1
)
ln
1...
Đọc tiếp
Cho hàm số f(x) xác định trên ( - ∞ ; - 1 ) ∪ ( 0 ; + ∞ ) thỏa mãn f ' ( x ) = 1 x 2 + x , f ( 1 ) = ln 1 2 . Cho ∫ 1 2 ( x 2 + 1 ) 2 f ( x ) d x =a ln3+b ln2+c, với a,b,c là các số hữu tỷ. Giá trị biểu thức a+b+c bằng
A. 27 20
B. 23 20
C. - 27 20
D. - 23 20
Giả sử a ; b ; c là các số thỏa mãn a + b + c = 259 và \(\frac{1}{a+b}+\frac{1}{b+c}+\frac{1}{a+c}=15\)
Khi đó giá trị của biểu thức \(Q=\frac{a}{b+c}+\frac{b}{a+c}+\frac{c}{a+b}=\)
Bài 1: Cho B = \(x^{2013}-2014x^{2012}+2014x^{2011}-2014x^{2010}+...-2014x^2+2014x-1\)
Tính giá trị của biểu thức B với x=2013.
Bài 2: Cho các số a,b,c khác 0 thỏa mãn: \(\frac{ab}{a+b}=\frac{bc}{b+c}=\frac{ca}{c+a}\)
Tính giá trị của biểu thức : M=\(\frac{ab+bc+ca}{a^2+b^2+c^2}\)