Giúp mình ạ (giải thích giùm mình cx đc )



Những câu hỏi liên quan
Giúp mình câu này với ạ. Mình cảm ơn nhiều! (Nếu đc thì giải thích giùm mình nha)
Đọc tiếp
Giúp mình câu này với ạ. Mình cảm ơn nhiều! (Nếu đc thì giải thích giùm mình nha)
Pt có 2 nghiệm khi: \(\left\{{}\begin{matrix}m\ne0\\\Delta'=9\left(m-1\right)^2-9m\left(m-3\right)\ge0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m\ne0\\m\ge-1\end{matrix}\right.\)
Khi đó theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{6\left(m-1\right)}{m}\\x_1x_2=\dfrac{9\left(m-3\right)}{m}\end{matrix}\right.\)
\(x_1+x_2=x_1x_2\Rightarrow\dfrac{6\left(m-1\right)}{m}=\dfrac{9\left(m-3\right)}{m}\)
\(\Rightarrow6\left(m-1\right)=9\left(m-3\right)\)
\(\Rightarrow m=7\)
A đúng
Đúng 5
Bình luận (1)
Giúp mình câu này với ạ. Mình cảm ơn nhiều! (Nếu đc thì giải thích giùm mình nha)
Đọc tiếp
Giúp mình câu này với ạ. Mình cảm ơn nhiều! (Nếu đc thì giải thích giùm mình nha)
Giúp mình câu 11nhanh đc ko ạ, giải chi tiết giùm mình luôn ạ
Thể tích của vật là
`V_v = V_2-V_1 =175-130=45cm^3=4,5*10^(-5)m^3`
Do vật chìm hoàn toàn trong nước nên
Lực đẩy Ác si met t/d lên vật là
`F_A = V_v * d_n =4,5*10^(-5) *10000 =0,45(N)`
khối lg của vật ngoài ko khí là
`m=P/10=(P_n +F_A )/10= (4,2+0,45)/10 =0,465(kg)`
khối lg riêng vật là
`D=m/V_v = (0,465)/(4,5*10^(-5))=~~ 10333,3(kg//m^3)`
Đúng 1
Bình luận (0)
Giải giúp mình câu 8 ạ, phần a thôi cx đc ạ

a) Có \(\widehat{OAM}=90^0\) => Tam giác \(OAM\) nội tiếp đường tròn đường kính OM
=> O,A,M cùng thuộc đường tròn đường kính OM (*)
Có \(\widehat{OBM}=90^0\) => Tam giác \(OBM\) nội tiếp đường tròn đường kính OM
=> O,B,M cùng thuộc đường tròn đường kính OM (2*)
Do N là trung điểm của PQ => \(ON\perp PQ\)( Vì trong một đt, đường kính đi qua trung điểm của một dây ko đi qua tâm thì vuông góc với dây ấy)
=> \(\widehat{ONM}=90^0\) => Tam giác \(ONM\) nội tiếp đường tròn đường kính OM
=> O,N,M cùng thuộc đt đường kính OM (3*)
Từ (*) (2*) (3*) => O,M,N,A,B cùng thuộc đt đk OM hay đt bán kính \(\dfrac{OM}{2}\)
b) Có AM//PS (cùng vuông góc với OA)
Gọi E là gđ của PS với (O) => \(sđ\stackrel\frown{AE}=sđ\stackrel\frown{AP}\)
Có \(\widehat{PRB}=\dfrac{1}{2}\left(sđ\stackrel\frown{AE}+sđ\stackrel\frown{PB}\right)\)\(=\dfrac{1}{2}\left(sđ\stackrel\frown{AP}+sđ\stackrel\frown{PB}\right)=\dfrac{1}{2}sđ\stackrel\frown{AB}\)
=> \(\widehat{PRB}=\widehat{MAB}=\dfrac{1}{2}sđ\stackrel\frown{AB}\)
Có BNAM nội tiếp => \(\widehat{MAB}=\widehat{MNB}\)
\(\Rightarrow\widehat{PRB}=\widehat{MNP}\) => PRNB nội tiếp
\(\Rightarrow\widehat{BRN}=\widehat{BPN}\) mà \(\widehat{BPN}=\widehat{BAQ}=\dfrac{1}{2}sđ\stackrel\frown{BQ}\)
\(\Rightarrow\widehat{BRN}=\widehat{BAQ}\) => RN//AQ hay RN // SQ mà N la trung điểm của PQ
=> RN là đường TB của tam giác PSQ
=> R là trung điểm của PS <=> PR=RS
Đúng 2
Bình luận (0)
Làm giúp mình với, mấy câu tính toán giải thích chi tiết ra giùm ạ chứ mình search mạng rồi nhưng không hiểu, làm được hay câu ấy

1/2+1/6+1/12+1/20+...+1/132
ai giúp mình đc ko ạ mình cần gấp nếu trả lời đc thì giải thích cho mình đc ko ạ?
\(\frac{1}{2}+\frac{1}{6}+\frac{1}{12}+\frac{1}{20}+...+\frac{1}{132}\)
\(=\frac{1}{1\cdot2}+\frac{1}{2\cdot3}+\frac{1}{3\cdot4}+\frac{1}{4\cdot5}+...+\frac{1}{11\cdot12}\)
\(=\frac{1}{1}-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+\frac{1}{4}-\frac{1}{5}+...+\frac{1}{11}-\frac{1}{12}\)
\(=\frac{1}{1}-\frac{1}{12}\)
\(=\frac{11}{12}\)
P/s : chả cần giải thick vì cái này nó sẵn cơ bản rồi.
\(\frac{1}{2}+\frac{1}{6}+\frac{1}{12}+\frac{1}{20}+...+\frac{1}{132}\)
\(=\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+\frac{1}{4.5}+...+\frac{1}{11.12}\)
\(=1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+\frac{1}{4}-\frac{1}{5}+...+\frac{1}{11}-\frac{1}{12}\)
\(=1-\frac{1}{12}=\frac{11}{12}\)
\(\frac{1}{2}\)
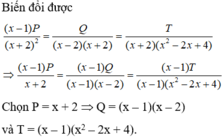
mọi ng ai giải thích giúp mình bước 2 đc ko ạ
`((x-1)P)/(x+2)^2=Q/((x-2)(x+2))=T/((x+2)(x^2-2x+4))`
Nhân 2 vế với `x+2 ne 0` ta có:
`((x-1)P)/(x+2)=Q/(x-2)=T/(x^2-2x+4)`
Nhân cả tử và mẫu với `x-1 ne 0` ta có:
`((x-1)P)/(x+2)=((x-1)Q)/((x-1)(x-2))=((x-1)T)/((x-1)(x^2-2x+4))`
Đúng 1
Bình luận (0)
23ha56m2=........ha (giải thik ra giùm mình đc ko ạ cách giải )
bây giờ 23ha đổi ra ha thì bn cứ ghi 23, rồi đổi 56m2 ra ha là có kết quả
Đúng 0
Bình luận (0)
Ai giải thích giùm mình với ạ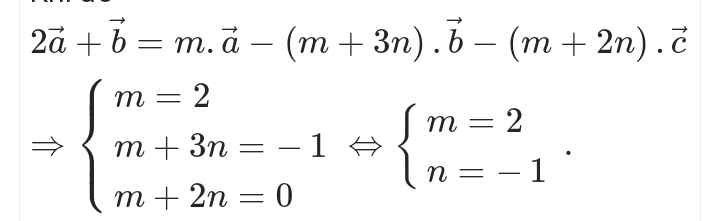
Đồng nhất hệ số 2 vế thôi, hệ số các vecto bên vế trái bằng với vế phải (bên vế trái ko có \(\overrightarrow{c}\) nên coi như hệ số của nó bằng 0, do đó \(-\left(2m+n\right)=0\Rightarrow2m+n=0\))
Đúng 0
Bình luận (0)























