Cho tam giác ABC vuông tại A có B ^ = 30 o . Khi đó:
A. A C = B C 2
B. A B = B C 2
C. Δ A B C là tam giác vuông cân
D. A C = B C 3
cho tam giác ABC vuông tại A có AC = 8, góc B = 30 độ. khi đó AB bằng
\(AB=\dfrac{AC}{\tan B}=\dfrac{8}{\tan30^0}=\dfrac{8}{\dfrac{\sqrt{3}}{3}}=8\sqrt{3}\)
trên tia đối tia AC lấy điểm D sao cho AD=AC
tam giác ABD =tam giác ABC(c.g.c) =>BD=BC
tam giác BDC cân có góc C=60 độ (A=90 do;B=30do)nen la tam giac deu
Do đó BC=DC =2AC=>AC=BC :2=4cm
(Bạn tự vẽ hình nha)
Xét tam giác ABC vuông tại A
Áp dụng hệ thức giữa cạnh và góc vào tam giác ta được:
AB=AC. CotB
=\(8\cdot Cot30\)
=\(8\sqrt{3}\)\(\approx13,86\)
a ) cho tam giác ABC vuông tại A , góc B = 30 độ
CMR : AC = 1/2 BC
b ) cho tam giác ABC vuông tại A có AB = 1/2 BC
CMR : góc C = 30 độ
Kẻ trung tuyến AM, AM = 1/2 BC = MB = MC
a) Nêu góc B = 30 độ thì góc C bằng 60 độ
Tam giác MAC cân tại M có góc C bằng 60 độ nên nó là tam giác đều => AC = MC = 1/2 BC
b) Nếu AC = 1/2 BC => Tam giác MAC đều vì AC = 1/2 BC = MC = MA
=> Góc C bằng 60 độ
Trong tam giác ABC có góc A = 90 độ, góc C = 60 độ => góc B = 30 độ
sao lại làm thế này
Cho tam giác ABC vuông tại A có AB < AC, đường cao AH. Gọi E,F là hình chiếu vuông góc của H lên AB,AC. Gọi O là chung điểm của BC.
a, CM tam giác ABH đồng dạng với tam giác AHE, từ đó chứng minh AH2 =AE.AB
b,CM tam giác ABC đồng dạng với tam giác AFE
c,Lấy A' đối xứng với A qua E, tia A'H cắt AC tại M và cắt AO tại N. Tính \(\frac{S_{AMN}}{S_{ACH}}\)khi góc C=30o
cho tam giác ABC vuông tại A có AB < AC, đường cao AH. Gọi E,F là hình chiếu vuông góc của H lên AB, AC. Gọi O là trung điểm của BC.
a, CM tam giác ABH đồng dạng với tam giác AHE, từ đó chứng minh AH2= AE.AB
b,CM tam giác ABC đồng dạng với tam giác AFE
c, Lấy A' đối xứng với A qua E, tia A'H cắt AC tại M và cắt AO tại N, tính tỉ số\(\frac{S_{AMN}}{S_{ACH}}\)khi góc C = 30o
Cho tam giác ABC vuông tại A có AC=6cm, góc B =30o
a) Giải tam giác vuông ABC
b) Vẽ đường cao Ah và trung tuyến Am của tam giác ABC. Tính diện tích tam giá AHM
tam giác ABC vuông tại A có BC = 10 cm ; B = 30 độ. Lấy D thuộc cạnh BC sao cho BAD = 15 độ. Khi đó CD = ...
- Tam giác ABC vuông tại A, Có góc ABC = 30 độ => tam giác ABC là nửa tam giác đều
=> AC = \(\frac{BC}{2}=\frac{10}{2}=5\)(cm) và AB= \(AB.\sqrt{3}=5\sqrt{3}\)(cm)
- Trên cạnh BC lấy điểm E sao cho AD là phân giác góc BAE. Kẻ EF vuông góc với AB (F thuộc AB)
- Dễ chứng minh tam giác AEC đều nên AE=AC=EC=5cm
- Do AD là phân giác của góc BAE nên: góc BAE = 2. góc BAD=2độ.15độ=30độ nên tam giác EAB cân tại E
=> AE=BE=5cm
Do EC=5 nên BE =BC - EC=10-5=5(cm)
- Do AD là phân giác của góc BAE nên:
\(\frac{BD}{AB}=\frac{DE}{AE}=\frac{BD+DE}{AB+AE}=\frac{BE}{AB+AE}=\frac{5}{5\sqrt{3}+5}\)=> DE=\(\frac{AE.5}{5\sqrt{3}+5}\left(doAE=5cm\right)\)
Vậy DC=DE+EC=\(\frac{5}{\sqrt{3}+1}+5=\frac{5+5\sqrt{3}}{2}cm\)
:)) Bạn xem xem sai chỗ nào không chứ sao số lẻ quá...
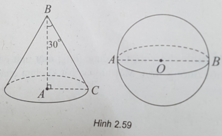
Cho tam giác ABC vuông tại A có BC = 2a và ∠ B = 30 ° . Quay tam giác vuông này quanh trục AB, ta được một hình nón đỉnh B. Gọi S 1 là diện tích toàn phần của hình nón đó và S 2 là diện tích mặt cầu đường kính AB. Khi đó, tỉ số S 1 / S 2 là:
A. 1 B. 1/2
C. 2/3 D. 3/2
Chọn A.
(h.2.59) Trong tam giác ABC vuông tại A, ta có:
AC = BC.sin30 ° = a;
AB = BC.cos30 ° = a 3 .
Diện tích toàn phần hình nón là:
S 1 = S xq + S đáy = πRl + πR 2 = πa . 2 a + πa 2 = 3 πa 2
Diện mặt cầu đường kính AB là:
S 2 = πAB 2 = π a 3 2 = 3 πa 2
Từ đó suy ra, tỉ số S 1 / S 2 = 1
Cho tam giác ABC vuông tại A có BC=a, CA=b, AB=c. Giải tam giác ABC biết: b=10cm, góc C=30 độ.
Cảm ơn rất nhiều ạ!
Ta có: ΔABC vuông tại A(gt)
nên \(\widehat{B}+\widehat{C}=90^0\)
hay \(\widehat{B}=60^0\)
Xét ΔABC vuông tại A có
\(AB=AC\cdot\tan30^0\)
\(\Leftrightarrow AB=10\cdot\dfrac{\sqrt{3}}{3}=\dfrac{10\sqrt{3}}{3}\left(cm\right)\)
Xét ΔABC vuông tại A có
\(\sin30^0=\dfrac{AB}{BC}\)
\(\Leftrightarrow BC=\dfrac{10\sqrt{3}}{3}:\dfrac{1}{2}=\dfrac{10\sqrt{3}}{3}\cdot2=\dfrac{20\sqrt{3}}{3}\left(cm\right)\)
Cho tam giác ABC vuông tại A có B = 60°. Trên cạnh BC lấy điểm M sao cho \(\widehat {CAM} = {30^o}\). Chứng minh rằng:
a) Tam giác CAM cân tại M;
b) Tam giác BAM là tam giác đều;
c) M là trung điểm của đoạn thẳng BC.
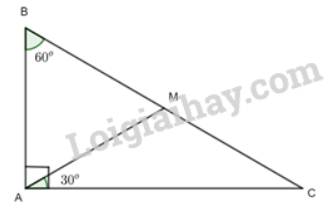
a) Xét tam giác ABC có:
\(\begin{array}{l}\widehat A + \widehat B + \widehat C = {180^o}\\ = > {90^o} + {60^o} + \widehat C = {180^o}\\ = > \widehat C = {30^o}\end{array}\)
Xét tam giác CAM có \(\widehat A = \widehat C = {30^o}\)
=>Tam giác CAM cân tại M.
b) Xét tam giác ABM có:
\(\begin{array}{l}\widehat C + \widehat {CMA} + \widehat {CAM} = {180^o}\\ = > {30^o} + \widehat {CMA} + {30^o} = {180^o}\\ = > \widehat {CMA} = {120^o}\\ = > \widehat {BMA} = {180^o} - \widehat {CMA} = {180^o} - {120^o} = {60^o}\end{array}\)
Xét tam giác ABM có:
\(\begin{array}{l}\widehat B + \widehat {BMA} + \widehat {BAM} = {180^o}\\ = > {60^o} + {60^o} + \widehat {BAM} = {180^o}\\ = > \widehat {BAM} = {60^o}\end{array}\)
Do \(\widehat {BAM} = \widehat {BMA} = \widehat {ABM} = {60^o}\) nên tam giác ABM đều.
c) Vì \(\Delta ABM\) đều nên \(AB = BM = AM\)
Mà \(\Delta CAM\) cân tại M nên MA = MC
Do đó, MB = MC. Mà M nằm giữa B và C
=> M là trung điểm của BC.