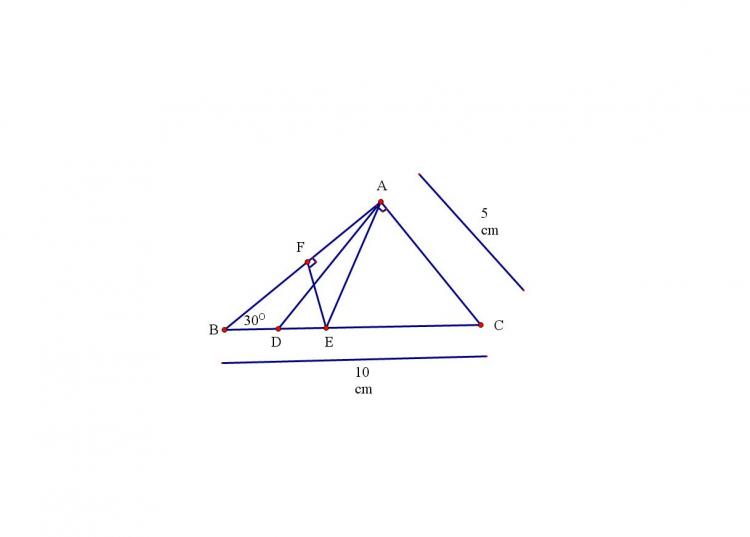
- Tam giác ABC vuông tại A, Có góc ABC = 30 độ => tam giác ABC là nửa tam giác đều
=> AC = \(\frac{BC}{2}=\frac{10}{2}=5\)(cm) và AB= \(AB.\sqrt{3}=5\sqrt{3}\)(cm)
- Trên cạnh BC lấy điểm E sao cho AD là phân giác góc BAE. Kẻ EF vuông góc với AB (F thuộc AB)
- Dễ chứng minh tam giác AEC đều nên AE=AC=EC=5cm
- Do AD là phân giác của góc BAE nên: góc BAE = 2. góc BAD=2độ.15độ=30độ nên tam giác EAB cân tại E
=> AE=BE=5cm
Do EC=5 nên BE =BC - EC=10-5=5(cm)
- Do AD là phân giác của góc BAE nên:
\(\frac{BD}{AB}=\frac{DE}{AE}=\frac{BD+DE}{AB+AE}=\frac{BE}{AB+AE}=\frac{5}{5\sqrt{3}+5}\)=> DE=\(\frac{AE.5}{5\sqrt{3}+5}\left(doAE=5cm\right)\)
Vậy DC=DE+EC=\(\frac{5}{\sqrt{3}+1}+5=\frac{5+5\sqrt{3}}{2}cm\)
:)) Bạn xem xem sai chỗ nào không chứ sao số lẻ quá...