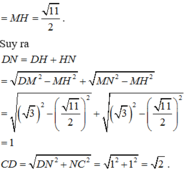Các câu hỏi tương tự
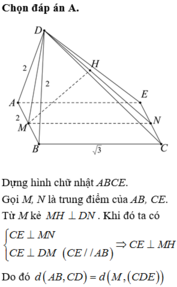
Cho tứ diện ABCD có tam giác ABD đều là cạnh bằng 2, tam giác ABC vuông tại B,
B
C
3
. Biết khoảng cách giữa hai đường thẳng chéo nhau AB và CD bằng
11
2
. Khi đó độ dài cạnh CD là A. 2 B. 1 C.
3
D.
2
Đọc tiếp
Cho tứ diện ABCD có tam giác ABD đều là cạnh bằng 2, tam giác ABC vuông tại B, B C = 3 . Biết khoảng cách giữa hai đường thẳng chéo nhau AB và CD bằng 11 2 . Khi đó độ dài cạnh CD là
A. 2
B. 1
C. 3
D. 2
Cho tứ diện ABCD có tam giác ABD đều cạnh bằng 2, tam giác ABC vuông tại B,
B
C
3
. Khoảng cách giữa hai đường thẳng AB và CD bằng
3
2
. Thể tích khối tứ diện ABCD bằng A.
3
2
B.
1
2
C....
Đọc tiếp
Cho tứ diện ABCD có tam giác ABD đều cạnh bằng 2, tam giác ABC vuông tại B, B C = 3 . Khoảng cách giữa hai đường thẳng AB và CD bằng 3 2 . Thể tích khối tứ diện ABCD bằng
A. 3 2
B. 1 2
C. 3 6
D. 1 6
Cho tứ diện ABCD có
A
D
⊥
A
B
C
,
ABC là tam giác vuông tại B. Biết
B
C
a
,
A
B
a
3
,
A
D
3
a
.
Quay các tam giác ABC và ABD xung quanh đường thẳng AB ta được 2 khối tròn xoay. Thể tích phần chung của 2 khối t...
Đọc tiếp
Cho tứ diện ABCD có A D ⊥ A B C , ABC là tam giác vuông tại B. Biết B C = a , A B = a 3 , A D = 3 a . Quay các tam giác ABC và ABD xung quanh đường thẳng AB ta được 2 khối tròn xoay. Thể tích phần chung của 2 khối tròn xoay đó bằng
A. 3 3 π a 3 16
B. 8 3 π a 3 3
C. 5 3 π a 3 16
D. 4 3 π a 3 16
1)Cho tứ giác ABCD các cạnh đoạn thẳng AC , BD cắt nhau tại điểm O , cho biết diện tích tam giác OAB , OBC , OCD lần lượt bằng 4cm2 , 3cm2 và 5,25cm2 . Hãy tính diện tích tứ giác ABCD .2)Cho hình tam giác ABC có góc A vuông , AB bằng 40cm , AC bằng 60cm . Hình ADEC là hình thang vuông có AD bằng 10cm .a) Tính diện tích tam giác BDEb)Tính diện tích hình thang ADECc)Tính diện tích hình tam giác ADE
Đọc tiếp
1)Cho tứ giác ABCD các cạnh đoạn thẳng AC , BD cắt nhau tại điểm O , cho biết diện tích tam giác OAB , OBC , OCD lần lượt bằng 4cm2 , 3cm2 và 5,25cm2 . Hãy tính diện tích tứ giác ABCD .
2)Cho hình tam giác ABC có góc A vuông , AB bằng 40cm , AC bằng 60cm . Hình ADEC là hình thang vuông có AD bằng 10cm .
a) Tính diện tích tam giác BDE
b)Tính diện tích hình thang ADEC
c)Tính diện tích hình tam giác ADE
Cho tứ diện ABCD có hai mặt ABC và ABD là các tam giác đều. Tính góc giữa hai đường thẳng AB và CD.
A. 30 °
B. 60 °
C. 90 °
D. 120 °
Cho hình tứ diện đều ABCD cạnh bằng a, gọi d là khoảng cách giữa hai đường thẳng AB và CD .Tìm d A. d(AB;CD)a B. d(AB;CD)a/3 C. d(AB;CD)a/2 D.
d
A
B
;
C
D
a
2
2
Đọc tiếp
Cho hình tứ diện đều ABCD cạnh bằng a, gọi d là khoảng cách giữa hai đường thẳng AB và CD .Tìm d
A. d(AB;CD)=a
B. d(AB;CD)=a/3
C. d(AB;CD)=a/2
D. d A B ; C D = a 2 2
Cho tứ diện ABCD có
A
B
A
D
B
C
B
D
,
A
B
a
,
C
D
a
30
. Khoảng cách giữa hai đường thẳng AB và CD bằng a. Tính khoảng cách h từ điểm cách đều 4 đỉnh A, B, C, D đến mỗi đỉnh đó. A.
h
a
13
2...
Đọc tiếp
Cho tứ diện ABCD có A B = A D = B C = B D , A B = a , C D = a 30 . Khoảng cách giữa hai đường thẳng AB và CD bằng a. Tính khoảng cách h từ điểm cách đều 4 đỉnh A, B, C, D đến mỗi đỉnh đó.
A. h = a 13 2
B. h = a 13 4
C. h = a 3 2
D. h = a 3 4
Cho tứ diện đều ABCD có tất cả các cạnh bằng a. Khoảng cách giữa hai đường thẳng AB và CD là: A.
a
2
2
B.
a
3
2
C.
a
3
3
D. a
Đọc tiếp
Cho tứ diện đều ABCD có tất cả các cạnh bằng a. Khoảng cách giữa hai đường thẳng AB và CD là:
A. a 2 2
B. a 3 2
C. a 3 3
D. a
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a,
A
B
C
^
60
°
. Mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt đáy. Gọi M và N lần lượt là trung điểm của các cạnh AB, CD. Khoảng cách giữa hai đường thẳng CM và SN bằng A.
a
3
4
B.
3...
Đọc tiếp
Cho hình chóp S.ABCD có đáy ABCD là hình thoi cạnh a, A B C ^ = 60 ° . Mặt bên SAB là tam giác đều và nằm trong mặt phẳng vuông góc với mặt đáy. Gọi M và N lần lượt là trung điểm của các cạnh AB, CD. Khoảng cách giữa hai đường thẳng CM và SN bằng
A. a 3 4
B. 3 a 2 2
C. a 3 2
D. 3 a 2