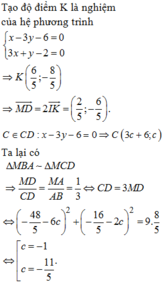Các câu hỏi tương tự
Trong mặt phẳng với hệ trục tọa độ Oxy cho tam giác ABC vuông tại A(2;1), đường thẳng BC: 4x-3y+50. P là một điểm di động trên cạnh AC (P khác A và C). Đường tròn đường kính PC cắt BP tại I sao cho: BP.BI + CP.CA25. Biết rằng B, C có tọa độ nguyên và C có hoành độ lớn hơn B. Hoành độ của điểm B là A.-2 B. -1 C. 1 D. 2
Đọc tiếp
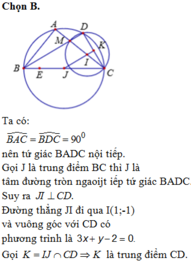
Trong mặt phẳng với hệ trục tọa độ Oxy cho tam giác ABC vuông tại A(2;1), đường thẳng BC: 4x-3y+5=0. P là một điểm di động trên cạnh AC (P khác A và C). Đường tròn đường kính PC cắt BP tại I sao cho: BP.BI + CP.CA=25. Biết rằng B, C có tọa độ nguyên và C có hoành độ lớn hơn B. Hoành độ của điểm B là
A.-2
B. -1
C. 1
D. 2
Trong không gian với hệ tọa độ Oxyz cho tam giác ABC vuông tại C có
A
B
C
^
60
°
;
A
B
3
2
. Đường thẳng AB có phương trình
x
-
3
1
y
-
4...
Đọc tiếp
Trong không gian với hệ tọa độ Oxyz cho tam giác ABC vuông tại C có A B C ^ = 60 ° ; A B = 3 2 . Đường thẳng AB có phương trình x - 3 1 = y - 4 1 = x + 8 - 4 , đường thẳng AC nằm trên mặt phẳng α : x + z - 1 = 0 . Biết điểm B là điểm có hoành độ dương, gọi (a,b,c) là tọa độ của điểm C. Giá trị a + b + c bằng
A. 2
B. 3
C. 4
D. 7
Trong không gian Oxyz, cho tam giác ABC vuông tại C,
A
B
C
^
60
°
,
A
B
3
2
.
Đường thẳng AB có phương trình
x
−
3
1
y
−
4
1...
Đọc tiếp
Trong không gian Oxyz, cho tam giác ABC vuông tại C, A B C ^ = 60 ° , A B = 3 2 . Đường thẳng AB có phương trình x − 3 1 = y − 4 1 = z + 8 − 4 , đường thẳng AC nằm trên mặt phẳng α : x + z − 1 = 0. Biết B là điểm có hoành độ dương, gọi a ; b ; c là tọa độ của điểm C, giá trị của a+b+c bằng
A. 3
B. 2
C. 4
D. 7
Trong hệ tọa độ Oxy. Cho đường tròn (C ) có phương trình
x
2
+
y
2
-
4
x
+
2
y
-
15
0
. I là tâm (C), đường thẳng d qua M(1;-3) cắt (C ) tại A, B. Biết tam giác IAB có diện tích là 8. Phương trình đường thẳng d là x+by+c0. Tính (b+c) A. 8. B. 2. C. 6 D. 1.
Đọc tiếp
Trong hệ tọa độ Oxy. Cho đường tròn (C ) có phương trình x 2 + y 2 - 4 x + 2 y - 15 = 0 . I là tâm (C), đường thẳng d qua M(1;-3) cắt (C ) tại A, B. Biết tam giác IAB có diện tích là 8. Phương trình đường thẳng d là x+by+c=0. Tính (b+c)
A. 8.
B. 2.
C. 6
D. 1.
Trong mặt phẳng với hệ tọa độ Oxy, cho đường tròn
C
:
x
+
1
2
+
y
-
2
2
9
và điểm
I
-
3
;
3
. Đường thẳng...
Đọc tiếp
Trong mặt phẳng với hệ tọa độ Oxy, cho đường tròn C : x + 1 2 + y - 2 2 = 9 và điểm I - 3 ; 3 . Đường thẳng ∆ : a x + b + c = 0 đi qua điểm I và cắt đường tròn (C) tại hai điểm A và B. Tiếp tuyến của A và B cắt nhau tại M. Biết điểm M thuộc đường thẳng x + 3 y - 4 = 0 . Tính P = 2 a + 3 b c
A. P = 1 3
B. P = - 11 4
C. P = 2 3
D. P = 1 4
1.Trên mp có 11 đường thẳng đôi 1 ko song song C/m:có 2 đường thẳng tạo với nhau 1 góc 17 độ2.Cho (O) đường kính AB.Lấy C ngoài đoạn thẳng AB (C nằm trên đường thẳng AB).Kẻ 2 tiếp tuyến CE và CF. AB cắt EF tại I, kẻ cát tuyến CMN. C/m: góc AIM góc BIN3.Cho tam giác ABC ngoại tiếp đường tròn (O).Biết D,E,F là các tiếp điểm , D thuộc AC, E thuộc AB, F thuộc BC Biết OEr, ABc, ACb, BCaC/m:a) (a+b+c)*r2S ( S là diện tích tam giác ABC)b)nếu (a+b+c)(a+b-c)4S thì tam giác ABC vuông
Đọc tiếp
1.Trên mp có 11 đường thẳng đôi 1 ko song song C/m:có 2 đường thẳng tạo với nhau 1 góc <17 độ
2.Cho (O) đường kính AB.Lấy C ngoài đoạn thẳng AB (C nằm trên đường thẳng AB).Kẻ 2 tiếp tuyến CE và CF. AB cắt EF tại I, kẻ cát tuyến CMN. C/m: góc AIM= góc BIN
3.Cho tam giác ABC ngoại tiếp đường tròn (O).Biết D,E,F là các tiếp điểm , D thuộc AC, E thuộc AB, F thuộc BC Biết OE=r, AB=c, AC=b, BC=a
C/m:a) (a+b+c)*r=2S ( S là diện tích tam giác ABC)
b)nếu (a+b+c)(a+b-c)=4S thì tam giác ABC vuông
Trong mặt phẳng tọa độ Oxy,cho đường thẳng
∆
:
x
-
y
0
. Đường tròn (C) có bán kính
R
10
cắt Δ tại hai điểm A, B sao cho
A
B
4
2
. Tiếp tuyến (C) tại A và B cắt nhau tại một điểm thuộc tia Oy. Phương trình đường tròn (C) là: A.
x
+
5...
Đọc tiếp
Trong mặt phẳng tọa độ Oxy,cho đường thẳng ∆ : x - y = 0 . Đường tròn (C) có bán kính R = 10 cắt Δ tại hai điểm A, B sao cho A B = 4 2 . Tiếp tuyến (C) tại A và B cắt nhau tại một điểm thuộc tia Oy. Phương trình đường tròn (C) là:
A. x + 5 2 + y + 3 2 = 10
B. x - 5 2 + y - 3 2 = 10
C. x - 3 2 + y - 5 2 = 10
D. x + 3 2 + y + 5 2 = 10
Trong mặt phẳng tọa độ Oxy cho đường tròn (C) có tâm I(1;-1) và bán kính R=5. Biết rằng đường thẳng ( d ) : 3 x - 4 y + 8 = 0 cắt đường tròn (C) tại hai điểm phân biệt A, B. Tính độ dài đoạn thẳng AB
A. 8
B. 4
C. 3
D. 6
Trong mặt phẳng tọa độ Oxy, cho đường tròn
C
1
:
x
2
+
y
2
4
,
C
2
:
x
2
+
y
2
-
12
x
+
18
0
và đường thẳng...
Đọc tiếp
Trong mặt phẳng tọa độ Oxy, cho đường tròn C 1 : x 2 + y 2 = 4 , C 2 : x 2 + y 2 - 12 x + 18 = 0 và đường thẳng d : x - y + 4 = 0 . Phương trình đường tròn có tâm thuộc C 2 , tiếp xúc với d và cắt C 1 tại hai điểm phân biệt A và B sao cho AB vuông góc với d là:
A. x - 3 2 + y - 3 2 = 4
B. x - 3 2 + y - 3 2 = 8
C. x + 3 2 + y + 3 2 = 8
D. x + 3 2 + y + 3 2 = 4