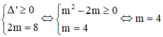Cho phương trình 3 x 2 - 4x + m = 0. Giá trị m để phương trình có các nghiệm x 1 , x 2 thỏa mãn x 1 - x 2 = 1 là:
A. m = -7/12
B. m = 7/12
C. m = 1
D. m = 1/3
Cho phương trình: x²-4x+m-5=0
Tìm tất cả các giá trị của m để phương trình có hai nghiệm phân biệt x1, x2 thỏa mãn: (x1-1)(x2²-3x2+m-6)=-3
Cho phương trình ẩn x: x2 – x + 1 + m = 0 (1)
a) Giải phương trình đã cho với m = 0.
b) Tìm các giá trị của m để phương trình (1) có hai nghiệm x1, x2 thỏa mãn: x1x2.( x1x2 – 2 ) = 3( x1 + x2 ).
a, Thay m=0 vào pt ta có:
\(x^2-x+1=0\)
\(\Rightarrow\) pt vô nghiệm
b, Để pt có 2 nghiệm thì \(\Delta\ge0\)
\(\Leftrightarrow\left(-1\right)^2-4.1\left(m+1\right)\ge0\\ \Leftrightarrow1-4m-4\ge0\\ \Leftrightarrow-3-4m\ge0\\ \Leftrightarrow4m+3\le0\\ \Leftrightarrow m\le-\dfrac{3}{4}\)
Theo Vi-ét:\(\left\{{}\begin{matrix}x_1+x_2=1\\x_1x_2=m+1\end{matrix}\right.\)
\(x_1x_2\left(x_1x_2-2\right)=3\left(x_1+x_2\right)\\ \Leftrightarrow\left(x_1x_2\right)^2-2x_1x_2=3.1\\ \Leftrightarrow\left(m+1\right)^2-2\left(m+1\right)-3=0\\ \Leftrightarrow\left[{}\begin{matrix}m+1=3\\m+1=-1\end{matrix}\right.\\ \Leftrightarrow\left[{}\begin{matrix}m=2\left(ktm\right)\\m=-2\left(tm\right)\end{matrix}\right.\)
Cho phương trình \(x^2-3x+m=0\) (1) (x là ẩn).
Tìm các giá trị m để phương trình (1) có 2 nghiệm phân biệt x1, x2 thỏa mãn \(\sqrt{x_1^2+1}+\sqrt{x_2^2+1}=3\sqrt{3}\).
\(\Delta=9-4m>0\Rightarrow m< \dfrac{9}{4}\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=3\\x_1x_2=m\end{matrix}\right.\)
\(\sqrt{x_1^2+1}+\sqrt{x_2^2+1}=3\sqrt{3}\)
\(\Leftrightarrow x_1^2+x_2^2+2+2\sqrt{\left(x_1^2+1\right)\left(x_2^2+1\right)}=27\)
\(\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2+2\sqrt{\left(x_1x_2\right)^2+\left(x_1+x_2\right)^2-2x_1x_2+1}=25\)
\(\Leftrightarrow9-2m+2\sqrt{m^2+9-2m+1}=25\)
\(\Leftrightarrow\sqrt{m^2-2m+10}=m+8\left(m\ge-8\right)\)
\(\Leftrightarrow m^2-2m+10=m^2+16m+64\)
\(\Rightarrow m=-3\) (thỏa mãn)
Pt trên có a=1, b=5, c=-3m+2
\(\Delta=b^2-4ac=25-4\cdot1\cdot\left(-3m+2\right)=17+12m\)
Để pt có hai nghiệm phân biệt thì \(\Delta>0\)<=> 17+12m >0 <=>m> 17/12
Theo hệ thức Viet, ta có:
\(\hept{\begin{cases}x_1+x_2=-5\\x_1\cdot x_2=-3m+2\end{cases}}\)
\(\left(x_1-x_2\right)^2=\left(x_1+x_2\right)^2-4x_1\cdot x_2=25-4\left(-3m+2\right)=17+12m=10\)
=> 12m = -7 <=>m=-7/12 (thỏa đkxđ)
Vậy với m=-7/12 thì phương trình có hai nghiệm x1, x2 thỏa (x1 - x2)^2 =10
Cho phương trình x^2 -4x+m-5=0 tìm các giá trị m để phương trình có 2 nghiệm phân biệt x1,x2 thoã mãn(x1-1).(x2^2-3x2+m-6)=-3
=>(x1-1)[x2^2-x2(x1+x2-1)+x1x2+1]=-3
=>(x1-1)[-x1x2+x2+x1x2+1]=-3
=>(x1-1)(x2+1)=-3
=>x1x2+(x1-x2)-1=-3
=>(x1-x2)=-3+1-x1x2=-2-m+5=-m+3
=>(x1+x2)^2-4x1x2=m^2-6m+9
=>4^2-4(m-5)=m^2-6m+9
=>4m-20=16-m^2+6m-9=-m^2+6m+7
=>4m-20+m^2-6m-7=0
=>m^2-2m-27=0
=>\(m=1\pm2\sqrt{7}\)
Cho phương trình bặc hai : (m + 2)x\(^2\)-2(m+1)x+m-4=0. Tìm các giá trị của m để phương trình :
a) có hai nghiệm dương phân biệt ;
b)Có hai nghiệm x\(_1\),x\(_2\) thỏa mãn : 3(x\(_1\)+x\(_2\)) =5x\(_1\).x\(_2\)
a.
Phương trình có 2 nghiệm dương pb khi:
\(\left\{{}\begin{matrix}m+2\ne0\\\Delta'=\left(m+1\right)^2-\left(m+2\right)\left(m-4\right)>0\\x_1+x_2=\dfrac{2\left(m+1\right)}{m+2}>0\\x_1x_2=\dfrac{m-4}{m+2}>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m\ne-2\\4m+9>0\\\dfrac{m+1}{m+2}>0\\\dfrac{m-4}{m+2}>0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m\ne-2\\m>-\dfrac{9}{4}\\\left[{}\begin{matrix}m>-1\\m< -2\end{matrix}\right.\\\left[{}\begin{matrix}m>4\\m< -2\end{matrix}\right.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}m>4\\-\dfrac{9}{4}< m< -2\end{matrix}\right.\)
b.
Pt có 2 nghiệm khi: \(\left\{{}\begin{matrix}m\ne-2\\\Delta'=4m+9\ge0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}m\ne-2\\m\ge-\dfrac{9}{4}\end{matrix}\right.\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=\dfrac{2\left(m+1\right)}{m+2}\\x_1x_2=\dfrac{m-4}{m+2}\end{matrix}\right.\)
\(3\left(x_1+x_2\right)=5x_1x_2\)
\(\Leftrightarrow\dfrac{6\left(m+1\right)}{m+2}=\dfrac{5\left(m-4\right)}{m+2}\)
\(\Rightarrow6\left(m+1\right)=5\left(m-4\right)\)
\(\Leftrightarrow m=-26< -\dfrac{9}{4}\left(loại\right)\)
Vậy ko tồn tại m thỏa mãn yêu cầu
Cho phương trình : \(x^2-\left(m+2\right)x-m-3=0\) (1)
a, Giải phương trình khi m = -1
b, Tìm giá trị của m để phương trình (1) có 2 nghiệm \(x_1,x_2\) thỏa mãn \(x^2_1+x_2^2>1\)
a: Khi m=-1 thì pt sẽ là \(x^2-\left(-1+2\right)x-\left(-1\right)-3=0\)
\(\Leftrightarrow x^2-x-2=0\)
=>x=2 hoặc x=-1
b: \(\Delta=\left(m+2\right)^2-4\left(-m-3\right)\)
\(=m^2+4m+4+4m+12\)
\(=m^2+8m+16=\left(m+4\right)^2\)
=>Phương trình luôn có hai nghiệm
Theo đề, ta có: \(\left(x_1+x_2\right)^2-2x_1x_2>1\)
\(\Leftrightarrow\left(m+2\right)^2-2\left(-m-3\right)>1\)
\(\Leftrightarrow m^2+4m+4+2m+6-1>0\)
\(\Leftrightarrow\left(m+3\right)^2>0\)
=>m<>-3
2.Cho phương trình \(x^{2+}2\left(m+1\right)x+m^2+4m+3=0\) (1),với m là tham số.Tìm các giá trị của m để phương trình (1) có 2 nghiệm x1 ;x2 thỏa mãn \(2x_1+2x_2-x_1x_2+7=0\)
Bài 2:
Ta có: \(\text{Δ}=\left(2m+2\right)^2-4\cdot\left(m^2+4m+3\right)\)
\(=4m^2+8m+4-4m^2-16m-12\)
\(=-8m-8\)
Để phương trình có hai nghiệm phân biệt thì Δ>0
hay m<-1
Áp dụng hệ thức Vi-et, ta được:
\(\left\{{}\begin{matrix}x_1+x_2=-2m-2\\x_1x_2=m^2+4m+3\end{matrix}\right.\)
Ta có: \(2x_1+2x_2-x_1x_2+7=0\)
\(\Leftrightarrow2\left(x_1+x_2\right)-x_1x_2+7=0\)
\(\Leftrightarrow2\cdot\left(-2m-2\right)-m^2-4m-3+7=0\)
\(\Leftrightarrow-4m-4-m^2-4m+4=0\)
\(\Leftrightarrow m\left(m+8\right)=0\)
\(\Leftrightarrow m=-8\)
Ta có: \(\Delta'=m^2+2m+1-m^2-4m-3=-2m-2\)
Để PT có 2 nghiệm thì \(-2m-2\ge0\Leftrightarrow m\le-1\)
Theo viet \(\left\{{}\begin{matrix}x_1+x_2=-2m-2\\x_2x_2=m^2+4m+3\end{matrix}\right.\)
theo bài
\(2x_1+2x_2-x_1x_2+7=0\)
\(\Leftrightarrow2\left(x_1+x_2\right)-x_1x_2+7=0\)
Thay số:
\(2\left(-2m-2\right)-m^2-4m-3+7=0\)
\(\Leftrightarrow-m^2-8m=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m=-8\\m=0\left(loai\right)\end{matrix}\right.\)
Vậy ...
Chúc bạn học tốt
cho phương trình x^2 - x + 1 +m = 0 tìm các giá trị của m để phương trình trên có hai nghiệm x1, x2 thỏa mãn x1*x2*(x1*x2 - 2) = 3*(x1 + x2)
Theo hệ thức Vi-ét ta có:
x1+x2=\(-\frac{-1}{1}=1\)
x1x2=\(\frac{1+m}{1}=1+m\)
=> x1x2(x1x2-2)=3(x1+x2)
<=> (1+m)(1+m-2)=3
<=> m2-1=3
<=>m2=4
<=> m=-2 hoặc m =2 (loại)
Vậy m = -2
Bài 2: cho phương trình\(x^2-2\left(m+1\right)x+2m+10=0\)
a)Tìm m để phương trình có nghiệm này gấp 3 lần nghiệm kia
b)Tìm m để phương trình có 2 nghiệm thỏa mãn \(P=-x_1^2-x_2^2-10x_1x_2\) có giá trị lớn nhất
\(\Delta'=\left(m+1\right)^2-\left(2m+10\right)=m^2-9\ge0\Rightarrow\left[{}\begin{matrix}m\ge3\\m\le-3\end{matrix}\right.\)
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=2\left(m+1\right)\\x_1x_2=2m+10\end{matrix}\right.\)
a. \(\left\{{}\begin{matrix}x_1+x_2=2\left(m+1\right)\\x_1=3x_2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}4x_2=2\left(m+1\right)\\x_1=3x_2\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x_2=\dfrac{m+1}{2}\\x_1=\dfrac{3\left(m+1\right)}{2}\end{matrix}\right.\)
Lại có \(x_1x_2=2m+10\Rightarrow\left(\dfrac{m+1}{2}\right)\left(\dfrac{3\left(m+1\right)}{2}\right)=2m+10\)
\(\Leftrightarrow3m^2+6m+3=8m+40\)
\(\Leftrightarrow3m^2-2m-37=0\Rightarrow m=\dfrac{1\pm4\sqrt{7}}{3}\)
b.
\(P=-\left(x_1+x_2\right)^2-8x_1x_2\)
\(=-4\left(m+1\right)^2-8\left(2m+10\right)\)
\(=-4m^2-24m-84=-4\left(m+3\right)^2-48\le-48\)
\(P_{max}=-48\) khi \(m=-3\)
a) Ta có: \(\Delta=\left[-2\left(m+1\right)\right]^2-4\cdot1\cdot\left(2m+10\right)\)
\(=\left(2m+2\right)^2-4\left(2m+10\right)\)
\(=4m^2+8m+4-8m-40\)
\(=4m^2-36\)
Để phương trình có nghiệm thì \(4m^2-36\ge0\)
\(\Leftrightarrow4m^2\ge36\)
\(\Leftrightarrow m^2\ge9\)
\(\Leftrightarrow\left[{}\begin{matrix}m\ge3\\m\le-3\end{matrix}\right.\)
Khi \(m\ge3\) hoặc \(m\le-3\) thì Áp dụng hệ thức Vi-et, ta được:
\(\left\{{}\begin{matrix}x_1\cdot x_2=2m+10\\x_1+x_2=2\left(m+1\right)=2m+2\end{matrix}\right.\)
mà \(x_1-3x_2=0\) nên ta lập được hệ phương trình:
\(\left\{{}\begin{matrix}x_1+x_2=2m+2\\x_1-3x_2=0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4x_2=2m+2\\x_1=3x_2\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_1=3\cdot x_2\\x_2=\dfrac{m+1}{2}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_1=\dfrac{3m+3}{2}\\x_2=\dfrac{m+1}{2}\end{matrix}\right.\)
Thay \(x_1=\dfrac{3m+3}{2};x_2=\dfrac{m+1}{2}\) vào \(x_1\cdot x_2=2m+10\), ta được:
\(\dfrac{3m+3}{2}\cdot\dfrac{m+1}{2}=2m+10\)
\(\Leftrightarrow\dfrac{3\left(m+1\right)^2}{4}=2m+10\)
\(\Leftrightarrow3\left(m^2+2m+1\right)=8m+40\)
\(\Leftrightarrow3m^2+6m+3-8m-40=0\)
\(\Leftrightarrow3m^2-2m-37=0\)
\(\Delta=\left(-2\right)^2-4\cdot3\cdot\left(-37\right)=4+444=448>0\)
Vì \(\Delta>0\) nên phương trình có hai nghiệm phân biệt là:
\(\left\{{}\begin{matrix}m_1=\dfrac{2+8\sqrt{7}}{6}=\dfrac{4\sqrt{7}+1}{3}\left(nhận\right)\\m_2=\dfrac{2-8\sqrt{7}}{6}=\dfrac{1-4\sqrt{7}}{3}\left(nhận\right)\end{matrix}\right.\)
Giá trị của tham số m để phương trình 4 x - m . 2 ( x + 1 ) + 2 m = 0 có 2 nghiệm x 1 , x 2 thỏa mãn x 1 + x 2 = 3 là
A. m = 2
B. m = 3
C. m = 1
D. m = 4
Đáp án D
Phương pháp:
Đặt 2x = t, t > 0. Chuyển về bài toán tìm m để phương trình bậc 2 ẩn t có 2 nghiệm t1, t2 thỏa mãn t1.t2 = 8
Cách giải:

Để phương trình (1) có 2 nghiệm x1, x2 thỏa mãn x1 + x2 = 3 thì phương trình (2) có 2 nghiệm t1,t2 thỏa mãn t1.t2 = 2x1.2x2 = 2x1 + x2 = 23 = 8
Khi đó: