a) Xét tính liên tục của hàm số y = g ( x ) tại x 0 = 2 , biết: g x = x 3 - 8 x - 2 n ế u x ≠ 2 5 n ế u x = 2
b.Trong biểu thức g(x) ở trên, cần thay số 5 bởi số nào đó để hàm số liên tục tại x 0 = 2 .
Xét các số thực x>b>a>0. Cho hàm số y=f(x) có đạo hàm liên tục trên R và có bảng xét dấu của đạo hàm như hình vẽ. Đặt g x = f x 3 Số điểm cực trị của hàm số y=g(x) là
![]()
A. 3
B. 7
C. 4
D. 5
Cho hàm số \(f\left( x \right) = \left\{ \begin{array}{l}{x^2} + x + 1,\,\,x \ne 4\\2a + 1,\,\,x = 4\end{array} \right.\)
a) Với a = 0, xét tính liên tục của hàm số tại x = 4.
b) Với giá trị nào của a thì hàm số liên tục tại x = 4?
c) Với giá trị nào của a thì hàm số liên tục trên tập xác định của nó?
a) Với a = 0, tại x = 4, ta có:
\(\begin{array}{l}\mathop {\lim }\limits_{x \to 4} f\left( x \right) = \mathop {\lim }\limits_{x \to 4} \left( {{x^2} + x + 1} \right) = {4^2} + 4 + 1 = 21\\f\left( 4 \right) = 2.0 + 1 = 1\\ \Rightarrow \mathop {\lim }\limits_{x \to 4} f\left( x \right) \ne f\left( 4 \right)\end{array}\)
Do đó hàm số không liên tục tại x = 4.
b) Ta có:
\(\begin{array}{l}\mathop {\lim }\limits_{x \to 4} f\left( x \right) = \mathop {\lim }\limits_{x \to 4} \left( {{x^2} + x + 1} \right) = {4^2} + 4 + 1 = 21\\f\left( 4 \right) = 2a + 1\end{array}\)
Để hàm số liên tục tại x = 4 thì \(\mathop {\lim }\limits_{x \to 4} f\left( x \right) = f\left( 4 \right)\)
\(\begin{array}{*{20}{l}}{ \Leftrightarrow \;21{\rm{ }} = {\rm{ }}2a{\rm{ }} + {\rm{ }}1}\\{ \Leftrightarrow \;2a{\rm{ }} = {\rm{ }}20}\\{ \Leftrightarrow \;a{\rm{ }} = {\rm{ }}10}\end{array}\)
Vậy với a = 10 thì hàm số liên tục tại x = 4.
c) TXĐ: \(\mathbb{R}\)
Với \(x\; \in \;\left( {-{\rm{ }}\infty ;{\rm{ }}4} \right)\) có \(f\left( x \right) = {x^2} + x + 1\) liên tục với mọi x thuộc khoảng này.
Với \(x\; \in \;\left( {4;{\rm{ }} + \infty } \right)\) có \(f\left( x \right) = 2a + 1\) liên tục với mọi x thuộc khoảng này.
Do đó hàm số \(f\left( x \right)\) liên tục trên \(\mathbb{R}\) khi hàm số \(f\left( x \right)\) liên tục tại điểm x = 4 khi a = 10.
Vậy với a = 10 hàm số liên tục trên tập xác định của nó.
Ý kiến sau đúng hay sai ?
"Nếu hàm số y = f(x) liên tục tại điểm x0 còn hàm số y = g(x) không liên tục tại x0, thì
y = f(x) + g(x) là một hàm số không liên tục tại x0."
Ý kiến đúng
Giả sử ngược lại y = f(x) + g(x) liên tục tại x0. Đặt h(x) = f(x) + g(x). Ta có g(x) = h(x) - f(x).
Vì y = h(x) và y = f(x) liên tục tại x0 nên hiệu của chúng là hàm số y = g(x) phải liên tục tại x0. Điều này trái với giả thiết là y = g(x) không liên tục tại x0.
Xét hai câu sau:
(1) Hàm số y = x x + 1 liên tục tại x= 0.
(2) Hàm số y = x x + 1 có đạo hàm tại x=0 .
Trong hai câu trên:
A. Chỉ có (2) đúng.
B. Chỉ có (1) đúng
C. Cả hai đều đúng.
D. Cả hai đều sai.
xét tính liên tục của hàm số
\(y=-2x^2-4x\) tại x = 3
\(\lim\limits_{x\rightarrow3}f\left(x\right)=\lim\limits_{x\rightarrow3}-2x^2-4x=-2\cdot3^2-4\cdot3=-18-12=-30\)
\(f\left(3\right)=-2\cdot3^2-4\cdot3=-30\)
=>\(\lim\limits_{x\rightarrow3}f\left(x\right)=f\left(3\right)\)
=>f(x) liên tục tại x=3
Lời giải:
$\lim\limits_{x\to 3}f(x)=\lim\limits_{x\to 3}(-2x^2-4x)=-30=f(3)$ nên hàm liên tục tại $x=3$>
Cho hàm số: y = f x = 3 - x 2 + 5 x 2 - 4 x ≠ ± 2 - 1 6 x = 2
- Xét tính liên tục của hàm số f(x) tại x= 2?
+) Ta có :
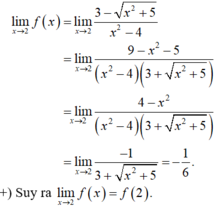
- Vậy hàm số đã cho liên tục tại x = 2.
Xét tính liên tục của các hàm số sau: g ( x ) = x - 1 2 - x - 1 n ế u x ≤ 1 - 2 x n ế u x ≥ 1 t ạ i x = 1
Hàm số: 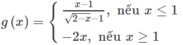
tại x = 1 có tập xác định là R
Ta có g(1) = -2 (1)
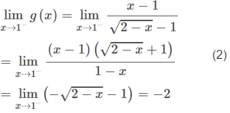
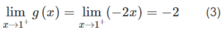
Từ (1), (2) và (3) suy ra
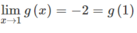
Vậy g(x) liên tục tại x = 1
Dùng định nghĩa xét tính liên tục của hàm số f(x)=x^3+2x-1 tại x0=3.
\(TXD:ℝ\)
Ta xét: \(lim_{x\rightarrow3}\left(x^3+2x-1\right)=3^3+2.3-1=32\)
mà \(f\left(3\right)=32\)
=> \(lim_{x\rightarrow3}\left(x^3+2x-1\right)=f\left(3\right)\)
=> hàm số liên tục tại x=3
Câu 1:
Cho f(x)= \(\dfrac{\sqrt{x+2}-\sqrt{2-x}}{x}\), x≠0. Phải bổ sung thêm giá trị f(0) bằng bao nhiêu thì hàm số f(x) liên tục tại x=0?
Câu 2:
Xét tính liên tục của hàm số
a, f(x)= \(\left\{{}\begin{matrix}x+\dfrac{3}{2}\\\dfrac{\sqrt{x+1}-1}{\sqrt[3]{1+x}-1}\end{matrix}\right.\)khi x≤0 và x>0 tại xo=0
b, f(x)= \(\left\{{}\begin{matrix}\dfrac{x^3-x^2+2x-2}{x-1}\\3x+a\end{matrix}\right.\)với x<1 và với x≥1, xo=1
1.
\(\lim\limits_{x\rightarrow0}\dfrac{\sqrt{x+2}-\sqrt{2-x}}{x}=\lim\limits_{x\rightarrow0}\dfrac{2x}{x\left(\sqrt{x+2}+\sqrt{2-x}\right)}=\lim\limits_{x\rightarrow0}\dfrac{2}{\sqrt{x+2}+\sqrt{2-x}}=\dfrac{2}{2\sqrt{2}}=\dfrac{\sqrt{2}}{2}\)
Vậy cần bổ sung \(f\left(0\right)=\dfrac{\sqrt{2}}{2}\) để hàm liên tục tại \(x=0\)
2.
a. \(f\left(0\right)=\lim\limits_{x\rightarrow0^-}f\left(x\right)=\lim\limits_{x\rightarrow0^-}\left(x+\dfrac{3}{2}\right)=\dfrac{3}{2}\)
\(\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^+}\dfrac{\sqrt{x+1}-1}{\sqrt[3]{1+x}-1}=\lim\limits_{x\rightarrow0^+}\dfrac{x\left(\sqrt[3]{\left(x+1\right)^2}+\sqrt[3]{x+1}+1\right)}{x\left(\sqrt[]{x+1}+1\right)}\)
\(=\lim\limits_{x\rightarrow0^+}\dfrac{\sqrt[3]{\left(x+1\right)^2}+\sqrt[3]{x+1}+1}{\sqrt[]{x+1}+1}=\dfrac{3}{2}\)
\(\Rightarrow f\left(0\right)=\lim\limits_{x\rightarrow0^+}f\left(x\right)=\lim\limits_{x\rightarrow0^-}f\left(x\right)\) nên hàm liên tục tại \(x=0\)
2b.
\(\lim\limits_{x\rightarrow1^-}f\left(x\right)=\lim\limits_{x\rightarrow1^-}\dfrac{x^3-x^2+2x-2}{x-1}=\lim\limits_{x\rightarrow1^-}\dfrac{x^2\left(x-1\right)+2\left(x-1\right)}{x-1}\)
\(=\lim\limits_{x\rightarrow1^-}\dfrac{\left(x^2+2\right)\left(x-1\right)}{x-1}=\lim\limits_{x\rightarrow1^-}\left(x^2+2\right)=3\)
\(\lim\limits_{x\rightarrow1^+}f\left(x\right)=f\left(1\right)=\lim\limits_{x\rightarrow1^+}\left(3x+a\right)=a+3\)
- Nếu \(a=0\Rightarrow f\left(1\right)=\lim\limits_{x\rightarrow1^-}f\left(x\right)=\lim\limits_{x\rightarrow1^+}f\left(x\right)\) hàm liên tục tại \(x=1\)
- Nếu \(a\ne0\Rightarrow\lim\limits_{x\rightarrow1^-}f\left(x\right)\ne\lim\limits_{x\rightarrow1^+}f\left(x\right)\Rightarrow\) hàm không liên tục tại \(x=1\)