a) Ta có: g(2) = 5.
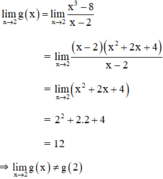
⇒ g(x) không liên tục tại x = 2.
b) Để g(x) liên tục tại x = 2
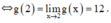
Vậy để hàm số liên tục tại x = 2 thì cần thay 5 bằng 12.
a) Ta có: g(2) = 5.
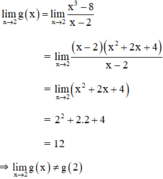
⇒ g(x) không liên tục tại x = 2.
b) Để g(x) liên tục tại x = 2
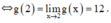
Vậy để hàm số liên tục tại x = 2 thì cần thay 5 bằng 12.
Câu 1:
Cho f(x)= \(\dfrac{\sqrt{x+2}-\sqrt{2-x}}{x}\), x≠0. Phải bổ sung thêm giá trị f(0) bằng bao nhiêu thì hàm số f(x) liên tục tại x=0?
Câu 2:
Xét tính liên tục của hàm số
a, f(x)= \(\left\{{}\begin{matrix}x+\dfrac{3}{2}\\\dfrac{\sqrt{x+1}-1}{\sqrt[3]{1+x}-1}\end{matrix}\right.\)khi x≤0 và x>0 tại xo=0
b, f(x)= \(\left\{{}\begin{matrix}\dfrac{x^3-x^2+2x-2}{x-1}\\3x+a\end{matrix}\right.\)với x<1 và với x≥1, xo=1
Cho hàm số: y = f x = 3 - x 2 + 5 x 2 - 4 x ≠ ± 2 - 1 6 x = 2
- Xét tính liên tục của hàm số f(x) tại x= 2?
Xét tính liên tục của các hàm số sau: g ( x ) = x - 1 2 - x - 1 n ế u x ≤ 1 - 2 x n ế u x ≥ 1 t ạ i x = 1
xét tính liên tục của hàm số
\(y=-2x^2-4x\) tại x = 3
Xét tính liên tục của các hàm số sau trên tập xác định của chúng g ( x ) = 1 - x x - 2 2 n ế u x ≠ 2 3 n ế u x = 2
Xét hai câu sau:
(1) Hàm số y = x x + 1 liên tục tại x= 0.
(2) Hàm số y = x x + 1 có đạo hàm tại x=0 .
Trong hai câu trên:
A. Chỉ có (2) đúng.
B. Chỉ có (1) đúng
C. Cả hai đều đúng.
D. Cả hai đều sai.
xét tính liên tục của hàm số sau tại x = 2
\(f\left(x\right)=\left\{{}\begin{matrix}-x^2+3x-2\\x+3\end{matrix}\right.\) khi \(x>2\); khi \(x\le2\)
xét tính liên tục của hàm số sau tại x = 2
\(f\left(x\right)=\left\{{}\begin{matrix}\dfrac{2x^2-7x+6}{2-x}\\2x-5\end{matrix}\right.\) khi \(x\ne2\); khi \(x=2\)
Xét tính liên tục của hàm số sau tại điểm x 0 = 2
f ( x ) = 2 x 2 - 3 x - 2 k h i x ≠ 2 3 2 k h i x = 2