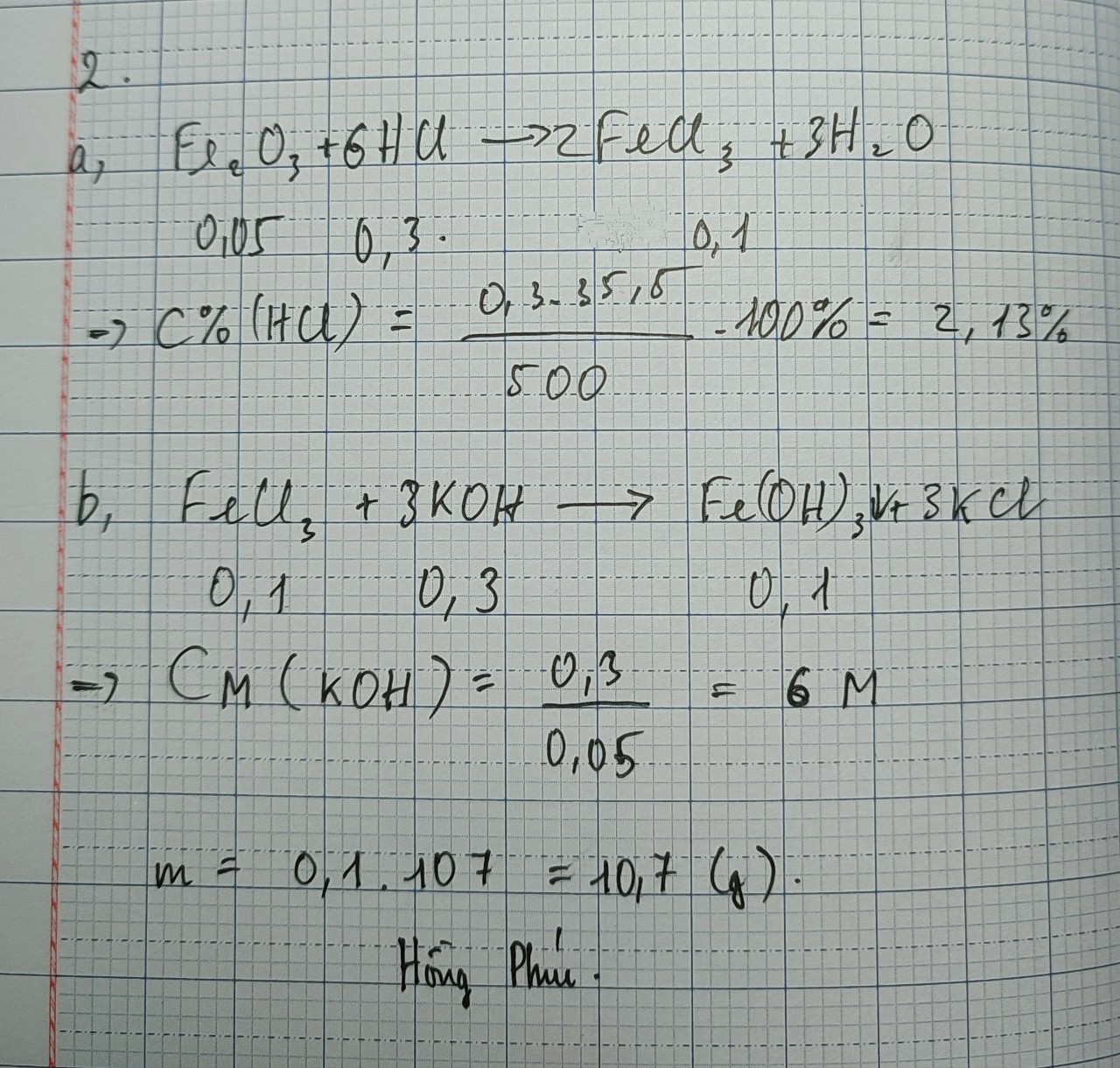Câu 2.

Trạng thái 1:

\(\left\{{}\begin{matrix}p_1=750mmHg\\V_1=50cm^3\\T_1=27^OC=300K\end{matrix}\right.\)

Trạng thái 2:

\(\left\{{}\begin{matrix}p_2=760mmHg\\V_2=???\\T_2=0^oC=273K\end{matrix}\right.\)

Áp dụng quá trình khí lí tưởng ta có:

\(\dfrac{p_1V_1}{T_1}=\dfrac{p_2V_2}{T_2}\)

\(\Rightarrow\dfrac{750\cdot50}{300}=\dfrac{760V_2}{273}\)

\(\Rightarrow V_{O_2}=V_2=44,9cm^3\)

1.

\(\dfrac{3\pi}{2}< a< 2\pi\Rightarrow sina< 0\)

\(\Rightarrow sin\alpha=-\sqrt{1-cos^2a}=-\dfrac{12}{13}\)

\(\Rightarrow tan2a=\dfrac{sin2a}{cos2a}=\dfrac{2sina.cosa}{cos^2a-sin^2a}=\dfrac{2.\left(-\dfrac{12}{13}\right).\left(\dfrac{5}{13}\right)}{\left(\dfrac{5}{13}\right)^2-\left(-\dfrac{12}{13}\right)^2}=...\)

3.

\(P=\dfrac{1}{x}+\dfrac{1}{y}=\dfrac{1}{x}+\dfrac{4}{4y}\ge\dfrac{\left(1+2\right)^2}{x+4y}=\dfrac{9}{6}=\dfrac{3}{2}\)

\(P_{min}=\dfrac{3}{2}\) khi \(\left(x;y\right)=\left(2;1\right)\)

4.

Lưu ý: hàm \(sinx\) đồng biến khi \(0< x< 90^0\) và nghịch biến khi \(90^0< x< 180^0\), hàm cos nghịch biến khi \(0< x< 90^0\)

Đường tròn (C) tâm \(I\left(1;1\right)\) bán kính \(R=4\) , \(\overrightarrow{IA}=\left(1;-1\right)\Rightarrow IA=\sqrt{2}\)

Theo công thức diện tích tam giác:

\(S_{IMN}=\dfrac{1}{2}IM.IN.sin\widehat{MIN}=\dfrac{1}{2}R^2.sin\widehat{MIN}=8.sin\widehat{MIN}\)

\(\Rightarrow S_{IMN}\) đạt max khi \(sin\widehat{MIN}\) đạt max

Gọi H là trung điểm MN \(\Rightarrow IH\perp MN\Rightarrow IH\le IA\) theo định lý đường xiên - đường vuông góc

\(\Rightarrow cos\widehat{HIM}=\dfrac{IH}{IM}\le\dfrac{IA}{IM}=\dfrac{\sqrt{2}}{4}\Rightarrow\widehat{HIM}>69^0\)

\(\Rightarrow\widehat{MIN}=2\widehat{HIM}>120^0>90^0\)

\(\Rightarrow sin\widehat{MIN}\) đạt max khi \(\widehat{MIN}\) đạt min

\(\Rightarrow\widehat{HIM}=\dfrac{1}{2}\widehat{MIN}\) đạt min

\(\Rightarrow cos\widehat{HIM}\) đạt max

\(\Rightarrow cos\widehat{HIM}=\dfrac{\sqrt{2}}{4}\Leftrightarrow H\) trùng A

Hay đường thẳng MN vuông góc IA \(\Rightarrow\) MN nhận (1;-1) là 1 vtpt

Phương trình MN: \(1\left(x-2\right)-1\left(y-0\right)=0\Leftrightarrow x-y-2=0\)

thi ?

Câu 1:

a: \(\sqrt{9\cdot25}=3\cdot5=15\)

b: \(=3\sqrt{2}\cdot\sqrt{2}+4\sqrt{2}\cdot\sqrt{2}-5\sqrt{2}\cdot\sqrt{2}\)

=6+8-10

=4

2.

Xét BPT: \(\left(x+3\right)\left(4-x\right)>0\Leftrightarrow-3< x< 4\) \(\Rightarrow D_1=\left(-3;4\right)\)

Xét BPT: \(x< m-1\) \(\Rightarrow D_2=\left(m-1;+\infty\right)\)

Hệ có nghiệm khi và chỉ khi \(D_1\cap D_2\ne\varnothing\)

\(\Leftrightarrow m-1< 4\)

\(\Leftrightarrow m< 5\)

3.

\(\dfrac{\pi}{24}=\dfrac{180^0}{24}=7^030'\)

4.

\(x^2+y^2-x+y+4=0\) không phải đường tròn

Do \(\left(\dfrac{1}{2}\right)^2+\left(-\dfrac{1}{2}\right)^2-4< 0\)

5.

\(f\left(x\right)=ax^2+bx+c\) có \(\left\{{}\begin{matrix}a\ne0\\\Delta=b^2-4ac< 0\end{matrix}\right.\) thì \(f\left(x\right)\) không đổi dấu trên R

6.

\(sin2020a=sin\left(2.1010a\right)=2sin1010a.cos1010a\)

7.

Công thức B sai

\(cos^2a+sin^2a=1\) , không phải \(cos2a\)

1.

\(cosA=\dfrac{b^2+c^2-a^2}{2bc}=\dfrac{1}{2}\Rightarrow\widehat{A}=60^o\)

\(S=\dfrac{1}{2}bc.sinA=\dfrac{1}{2}.8.5.sin60^o=10\sqrt{3}\)

\(S=\dfrac{1}{2}a.h_a=\dfrac{1}{2}.7.h_a=10\sqrt{3}\Rightarrow h_a=\dfrac{20\sqrt{3}}{7}\)

\(2R=\dfrac{a}{sinA}=\dfrac{7}{\dfrac{\sqrt{3}}{2}}=\dfrac{14\sqrt{3}}{3}\Rightarrow R=\dfrac{7\sqrt{3}}{3}\)

\(S=pr=\dfrac{a+b+c}{2}.r=10r=10\sqrt{3}\Rightarrow r=\sqrt{3}\)

\(m_a^2=\dfrac{b^2+c^2}{2}-\dfrac{a^2}{4}=\dfrac{129}{4}\Rightarrow m_a=\dfrac{\sqrt{129}}{2}\)

6.

a, Công thức trung tuyến:

\(AM^2=c^2=\dfrac{b^2+c^2}{2}-\dfrac{a^2}{4}=\dfrac{2b^2+2c^2-a^2}{4}\Rightarrow a^2=2\left(b^2-c^2\right)\)

b, \(a^2=2\left(b^2-c^2\right)\Rightarrow\dfrac{2\left(b^2-c^2\right)}{a^2}=1\)

\(\Leftrightarrow2\left(\dfrac{b^2}{a^2}-\dfrac{c^2}{a^2}\right)=1\)

\(\Leftrightarrow2\left(\dfrac{b^2}{a^2}.sin^2A-\dfrac{c^2}{a^2}.sin^2A\right)=sin^2A\)

\(\Leftrightarrow2\left(sin^2B-sin^2C\right)=sin^2A\)

Hay \(sin^2A=2\left(sin^2B-sin^2C\right)\)

Câu 7: Hình bạn tự vẽ

Giả sử hai trung tuyến \(AA_1;BB_1\) vuông góc với nhau. Gọi I là giao điểm của hai trung tuyến

Ta có: \(IA^2+IB^2=AB^2\)\(\Leftrightarrow\left(\dfrac{2}{3}m_a\right)^2+\left(\dfrac{2}{3}m_b\right)^2=c^2\)\(\Leftrightarrow4m_a^2+4m_b^2=9c^2\Leftrightarrow2\left(b^2+c^2\right)-a^2+2\left(a^2+c^2\right)-b^2=9c^2\Leftrightarrow a^2+b^2=5c^2\)(đúng với giả thiết)

suy ra giả sử là đúng . Vậy hai trung tuyến \(AA_1;BB_1\) vuông góc với nhau

1.

\(Na_2O+H_2O\rightarrow2NaOH\)

\(2NaOH+FeCl_2\rightarrow Fe\left(OH\right)_2\downarrow+2NaCl\)

\(Fe\left(OH\right)_2\rightarrow FeO+H_2O\)

\(FeO+2HCl\rightarrow FeCl_2+H_2O\)

1.C

2.D

3.C

4.C

5.C

6.C

7.D

8.D

9.C

10.D

11.A

12.A

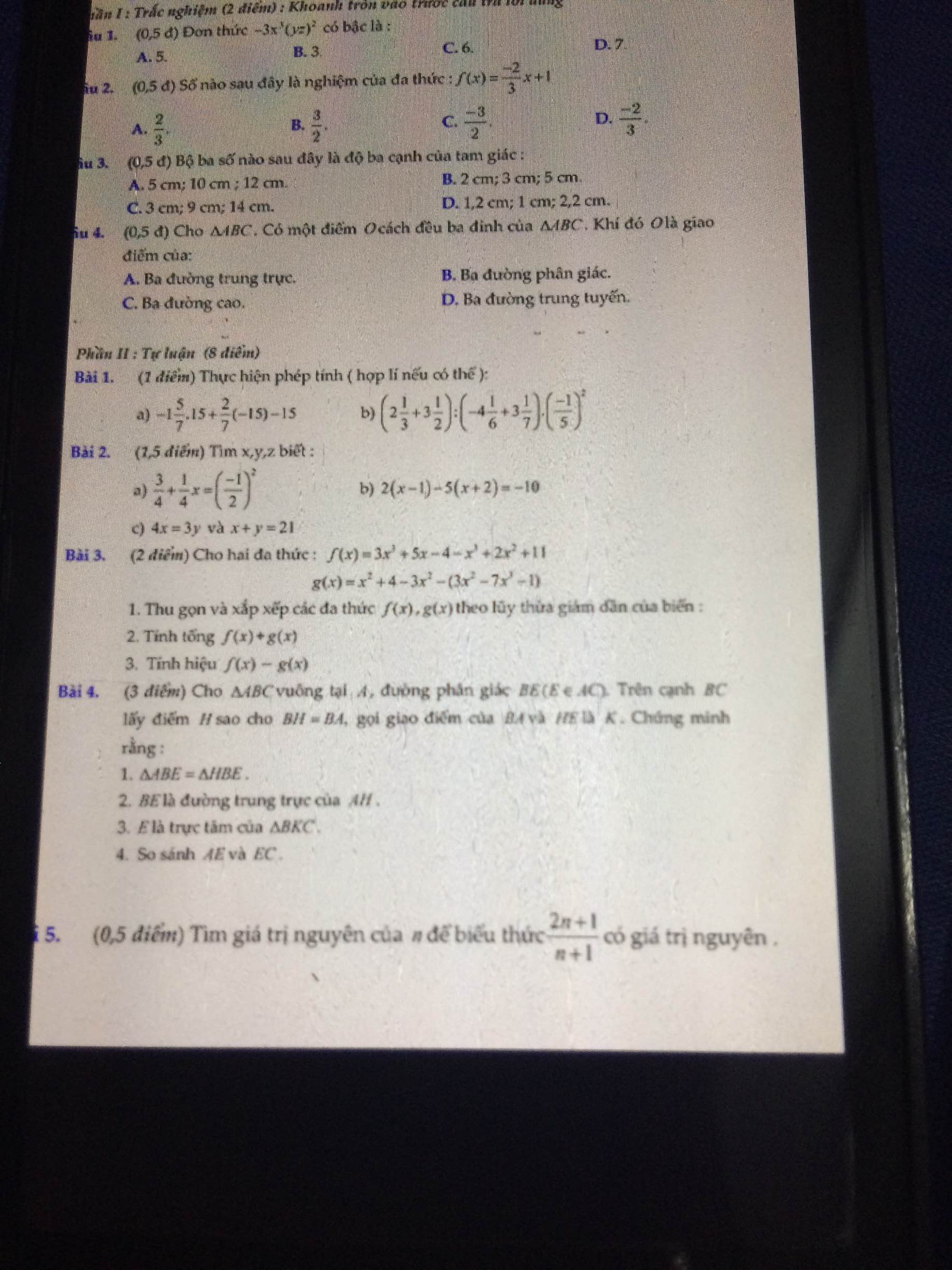
Bài 4: 

a) Xét ΔABE và ΔHBE có 

BA=BH(gt)

\(\widehat{ABE}=\widehat{HBE}\)(BE là tia phân giác của \(\widehat{ABH}\))

BE chung

Do đó: ΔABE=ΔHBE(c-g-c)

b) Ta có: ΔABE=ΔHBE(cmt)

nên EA=EH(hai cạnh tương ứng)

Ta có: BA=BH(gt)

nên B nằm trên đường trung trực của AH(Tính chất đường trung trực của một đoạn thẳng)(1)

Ta có: EA=EH(cmt)

nên E nằm trên đường trung trực của AH(Tính chất đường trung trực của một đoạn thẳng)(2)

Từ (1) và (2) suy ra BE là đường trung trực của AH

c) Ta có: ΔABE=ΔHBE(cmt)

nên \(\widehat{BAE}=\widehat{BHE}\)(hai góc tương ứng)

mà \(\widehat{BAE}=90^0\)(gt)

nên \(\widehat{BHE}=90^0\)

Xét ΔBKC có 

KH là đường cao ứng với cạnh BC

CA là đường cao ứng với cạnh BK

KH cắt CA tại E

Do đó: E là trực tâm của ΔBKC(Tính chất ba đường cao của tam giác)

d) Ta có: EA=EH(cmt)

mà EH<EC(ΔEHC vuông tại H có EC là cạnh huyền)

nên EA<EC