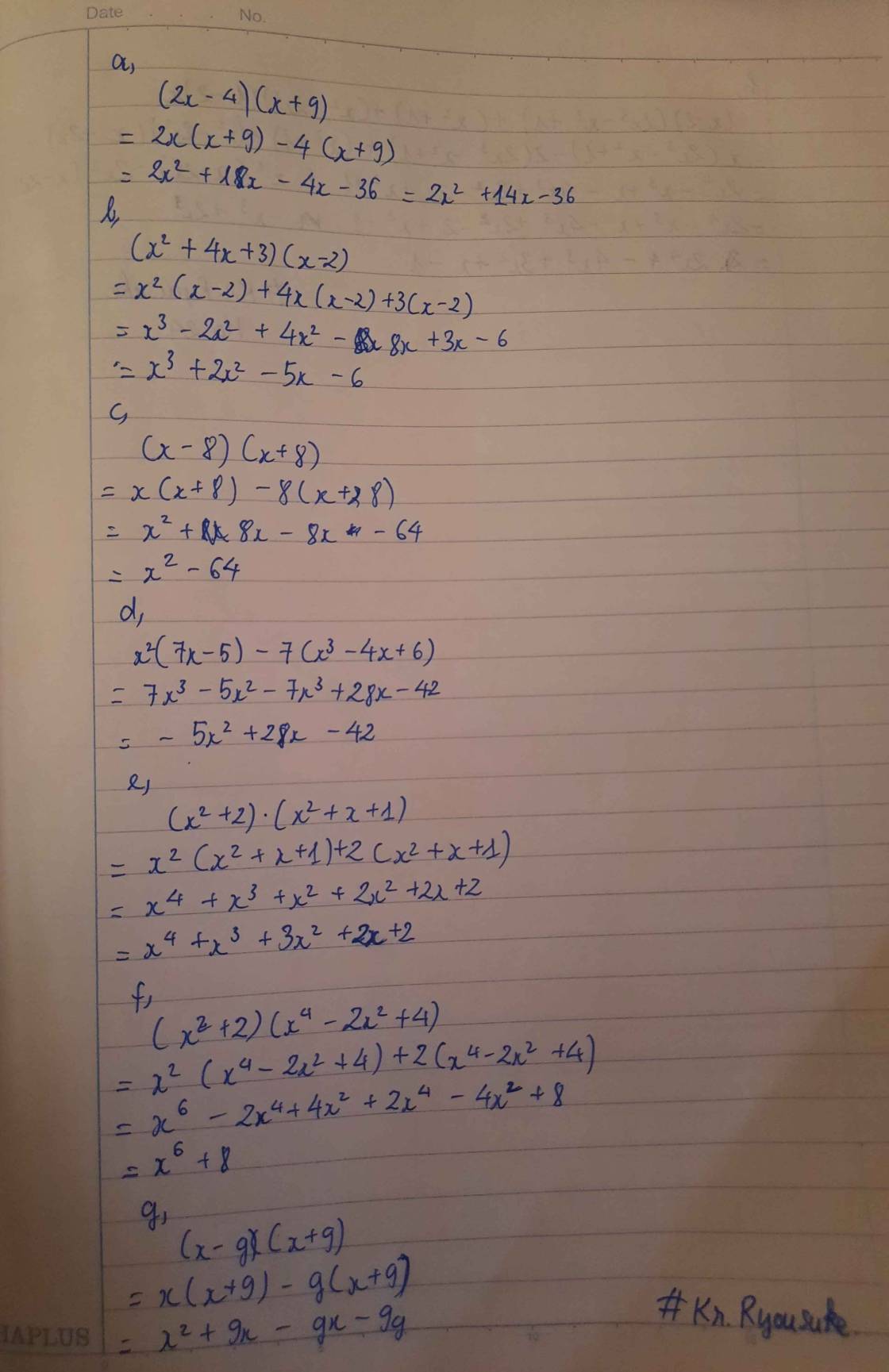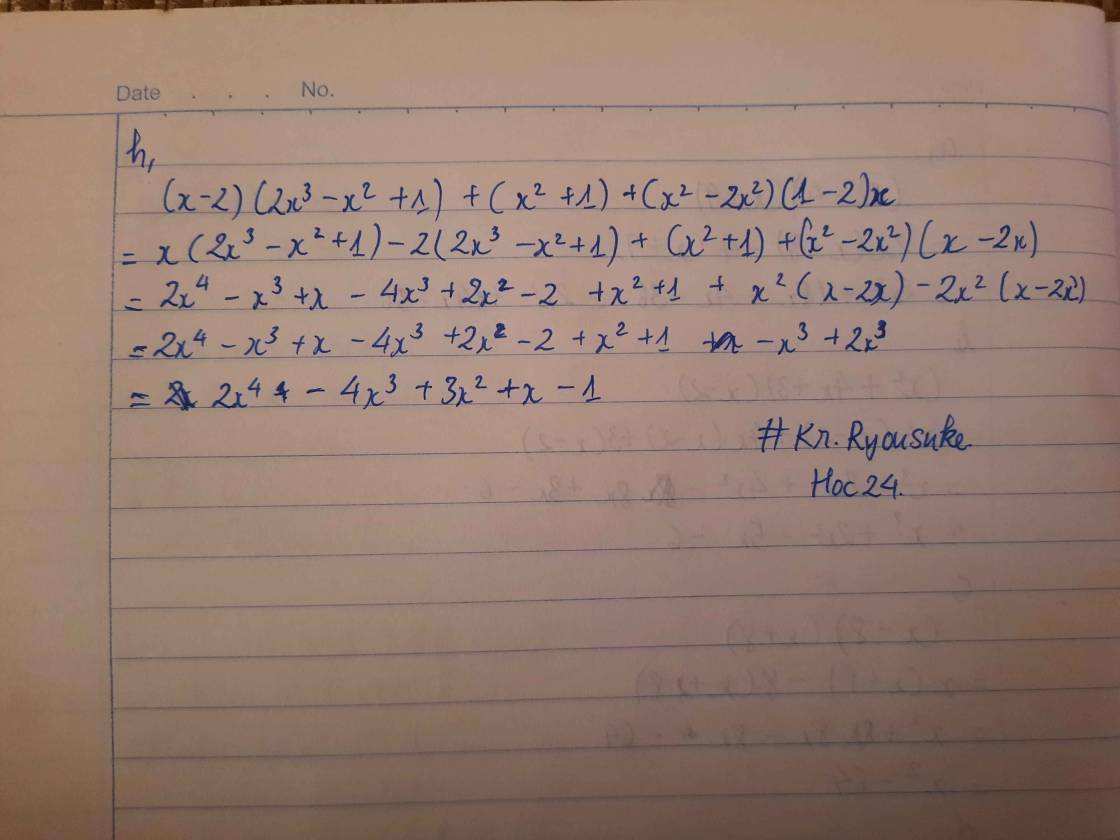a: \(=\dfrac{x^2+3x+2-x^2+2x+8}{\left(x-2\right)\left(x+2\right)}=\dfrac{5x+10}{\left(x-2\right)\left(x+2\right)}=\dfrac{5}{x-2}\)

b: \(=\dfrac{x^2-4x+3-x^2-3x-2+8x}{\left(x-1\right)\left(x+1\right)}=\dfrac{x+1}{\left(x-1\right)\left(x+1\right)}=\dfrac{1}{x-1}\)

c: \(=\dfrac{x+2}{x\left(x-2\right)}+\dfrac{2}{x\left(x+2\right)}+\dfrac{3x+2}{\left(x+2\right)\left(x-2\right)}\)

\(=\dfrac{x^2+2x+2x-4+3x+2}{x\left(x-2\right)\left(x+2\right)}=\dfrac{x^2+7x-2}{x\left(x-2\right)\left(x+2\right)}\)

a,

\(\dfrac{x+1}{x-2}-\dfrac{x}{x+2}+\dfrac{8}{x^2-4}\\ =\dfrac{x^2+3x+2-x^2+2x+8}{\left(x-2\right)\left(x+2\right)}=\dfrac{5x+10}{\left(x-2\right)\left(x+2\right)}=\dfrac{5\left(x+2\right)}{\left(x-2\right)\left(x+2\right)}=\dfrac{5}{x-2}\)

b,

\(\dfrac{x-3}{x+1}-\dfrac{x+2}{x-1}+\dfrac{8x}{x^2-1}\\ =\dfrac{x^2-4x+3-x^2-3x-2+8x}{\left(x-1\right)\left(x+1\right)}=\dfrac{x+1}{\left(x-1\right)\left(x+1\right)}\\ =\dfrac{1}{x-1}\)

a) x³y + x - y - 1

= (x³y - y) + (x - 1)

= y(x³ - 1) + (x - 1)

= y(x - 1)(x² + x + 1) + (x - 1)

= (x - 1)[y(x² + x + 1) + 1]

= (x - 1)(x²y + xy + y + 1)

b) x²(x - 2) + 4(2 - x)

= x²(x - 2) - 4(x - 2)

= (x - 2)(x² - 4)

= (x - 2)(x - 2)(x + 2)

= (x - 2)²(x + 2)

c) x³ - x² - 20x

= x(x² - x - 20)

= x(x² + 4x - 5x - 20)

= x[(x² + 4x) - (5x + 20)]

= x[x(x + 4) - 5(x + 4)]

= x(x + 4)(x - 5)

d) (x² + 1)² - (x + 1)²

= (x² + 1 - x - 1)(x² + 1 + x + 1)

= (x² - x)(x² + x + 2)

= x(x - 1)(x² + x + 2)

e) 6x² - 7x + 2

= 6x² - 3x - 4x + 2

= (6x² - 3x) - (4x - 2)

= 3x(2x - 1) - 2(2x - 1)

= (2x - 1)(3x - 2)

f) x⁴ + 8x² + 12

= x⁴ + 2x² + 6x² + 12

= (x⁴ + 2x²) + (6x² + 12)

= x²(x² + 2) + 6(x² + 2)

= (x² + 2)(x² + 6)

g) (x³ + x + 1)(x³ + x) - 2

Đặt u = x³ + x

x³ + x + 1 = u + 1

(u + 1).u - 2

= u² + u - 2

= u² - u + 2u - 2

= (u² - u) + (2u - 2)

= u(u - 1) + 2(u - 1)

= (u - 1)(u + 2)

= (x³ + x - 1)(x³ + x + 2)

= (x³ + x - 1)(x³ + x² - x² - x + 2x + 2)

= (x³ + x - 1)[(x³ + x²) - (x² + x) + (2x + 2)]

= (x³ + x - 1)[x²(x + 1) - x(x + 1) + 2(x + 1)]

= (x³ + x - 1)(x - 1)(x² - x + 2)

h) (x + 1)(x + 2)(x + 3)(x + 4) - 1

= [(x + 1)(x + 4)][(x + 2)(x + 3)] - 1

= (x² + 5x + 4)(x² + 5x + 6) - 1 (1)

Đặt u = x² + 5x + 4

u + 2 = x² + 5x + 6

(1) u.(u + 2) - 1

= u² + 2u - 1

= u² + 2u + 1 - 2

= (u² + 2u + 1) - 2

= (u + 1)² - 2

= (u + 1 + √2)(u + 1 - √2)

= (x² + 5x + 4 + 1 + √2)(x² + 5x + 4 + 1 - √2)

= (x² + 5x + 5 + √2)(x² + 5x + 5 - √2)

i: \(-\left(x^2+2\right)^2+4x\left(x^2+2\right)-3x^2\)

\(=-\left[\left(x^2+2\right)^2-4x\left(x^2+2\right)+3x^2\right]\)

\(=-\left[\left(x^2+2\right)^2-x\left(x^2+2\right)-3x\left(x^2+2\right)+3x^2\right]\)

\(=-\left[\left(x^2+2\right)\left(x^2+2-x\right)-3x\left(x^2+2-x\right)\right]\)

\(=-\left(x^2+2-x\right)\left(x^2-3x+2\right)\)

\(=-\left(x+2\right)\left(x-1\right)\left(x-2\right)\left(x-1\right)\)

\(=-\left(x+2\right)\left(x-2\right)\left(x-1\right)^2\)

l: \(81x^4+4y^4\)

\(=81x^4+36x^2y^2+4y^4-36x^2y^2\)

\(=\left(81x^4+36x^2y^2+4y^4\right)-\left(6xy\right)^2\)

\(=\left[\left(9x^2\right)^2+2\cdot9x^2\cdot2y^2+\left(2y^2\right)^2\right]-\left(6xy\right)^2\)

\(=\left(9x^2+2y^2\right)^2-\left(6xy\right)^2\)

\(=\left(9x^2+2y^2+6xy\right)\left(9x^2+2y^2-6xy\right)\)

\(b,=\left(x+8-x+2\right)^2=100\\ c,=x^2\left(x^2-16\right)-x^4+1=x^4-16x^2-x^4+1=1-16x^2\\ d,=x^3+1-x^3+1=2\)

b) \(=\left(x+8-x+2\right)^2=10^2=100\)

c) \(=x^2\left(x^2-16\right)-\left(x^4-1\right)=x^4-16x^2-x^4+1=1-16x^2\)

d) \(=x^3+1-x^3+1=2\)

Dễ

 Thế

Mà

Cũnhoir

Dc

Ạ

Chịu

Chắc

Phải

Ngu 

Lamqs

Mới

Hỏi

Câu

Này

Giúp mk vs

a: \(=x^3-2x^5\)

e: \(=x^4+2x^3-x^2-2x\)

Bài 5: 

a. 1 - 2y + y²

= (1 - y)²

b. (x + 1)² - 25

= (x + 1)² - 5²

= (x + 1 - 5)(x + 1 + 5)

= (x - 4)(x + 6)

c. 1 - 4x²

= 1² - (2x)²

= (1 - 2x)(1 + 2x)

d. 8 - 27x³

= 2³ - (3x)³

= (2 - 3x)(4 + 6x + 9x²)

e. (đề hơi khó hiểu ''x3'' !?)

g. x³ + 8y³

= (x + 2y)(x² - 2xy + y²)

\(1,\\ 12x^6y^3:4x^3y=3x^3y^2\\ \left(x+1\right)\left(x^2-x+1\right)=x^3+1\\ 2x^2y\left(x^2+3xy\right)=3x^4y+6x^3y^2\\ 2,\\ a,=2xy\left(2x+3y-4\right)\\ b,=\left(x-3\right)\left(x+y\right)\\ c,=\left(x-2\right)\left(x+2\right)+y\left(x-2\right)=\left(x+y+2\right)\left(x-2\right)\\ d,=x^2-2x-5x+10=\left(x-2\right)\left(x-5\right)\\ 3,\\ a,\Leftrightarrow x^2-x^2+2x=2\\ \Leftrightarrow2x=2\Leftrightarrow x=1\\ b,\Leftrightarrow\left(x-2\right)\left(x-2+1\right)=0\\ \Leftrightarrow\left(x-2\right)\left(x-1\right)=0\Leftrightarrow\left[{}\begin{matrix}x=1\\x=2\end{matrix}\right.\)

Bài 1: 

a: \(\Leftrightarrow x^2-5x+6< =0\)

=>(x-2)(x-3)<=0

=>2<=x<=3

b: \(\Leftrightarrow\left(x-6\right)^2< =0\)

=>x=6

c: \(\Leftrightarrow x^2-2x+1>=0\)

\(\Leftrightarrow\left(x-1\right)^2>=0\)

hay \(x\in R\)

c: \(=\dfrac{8}{\left(x^2+3\right)\left(x-1\right)\left(x+1\right)}+\dfrac{2x^2-2}{\left(x^2+3\right)\left(x-1\right)\left(x+1\right)}+\dfrac{\left(x^2+3\right)\left(x-1\right)}{\left(x^2+3\right)\left(x-1\right)\left(x+1\right)}\)

\(=\dfrac{1}{x-1}\)

\(A=6x^2+23x+21-\left(6x^2+23x-55\right)=76\\ B=x^4+x^3-x^2-2x^2-2x+2-x^4-x^3+3x^2+2x\\ =2\\ C=x^4+x^3-3x^2-2x-\left(x^4+x^3-x^2-2x^2-2x+2\right)\\ =-2\)