Cho đường thẳng d và đường tròn (O;R) không giao nhau. A là điểm trên (O). Xác định vị trí A để khoảng cách từ A đến đường thẳng d lớn nhất
Giúp mik với!!!
Những câu hỏi liên quan
Cho đường tròn (O) đường kính 10cm và đường thẳng d. Gọi H là hình chiếu vuông góc của O trên đường thẳng d. Biết OH 8cm. Xác định vị trí tương đối của đường thẳng d và đường tròn (O). A. Đường thẳng d và đường tròn (O) tiếp xúc nhau. B. Đường thẳng d và đường tròn (O) cắt nhau. C. Đường thẳng d và đường tròn (O) có điểm chung. D. Đường thẳng d và đường tròn(O) không có điểm chung.
Đọc tiếp
Cho đường tròn (O) đường kính 10cm và đường thẳng d. Gọi H là hình chiếu vuông góc của O trên đường thẳng d. Biết OH = 8cm. Xác định vị trí tương đối của đường thẳng d và đường tròn (O).
A. Đường thẳng d và đường tròn (O) tiếp xúc nhau.
B. Đường thẳng d và đường tròn (O) cắt nhau.
C. Đường thẳng d và đường tròn (O) có điểm chung.
D. Đường thẳng d và đường tròn(O) không có điểm chung.
a) Kẻ OH ⊥⊥ d
=> OH là khoảng cách từ d tới tâm đường tròn (O)
mà OH < R (3 < 5)
=> Đường thẳng d cắt đường tròn (O)
b) Xét ΔΔOAH vuông tại H có:
OH2+AH2=OA2OH2+AH2=OA2 (ĐL Pi-ta-go)
=> AH=OA2−OH2−−−−−−−−−−√=52−32−−−−−−√=4(cm)AH=OA2−OH2=52−32=4(cm)
Xét (O): AB là dây, OH ⊥⊥ AB
=> H trung điểm AB (quan hệ ⊥⊥ giữa đường kính và dây cung)
=> AB = 2AH = 8(cm)
c) Xét ΔΔABC có: O, H trung điểm AC, AB
=> OH là đường trung bình ΔΔABC
=> OH // BC mà OH ⊥⊥ AH
=> BC ⊥⊥ AH => ΔΔABC vuông tại B
=> AB2 + BC2 = AC2
=> BC=102−82−−−−−−−√=6(cm)BC=102−82=6(cm)
Xét ΔΔABC vuông tại B
có: sinC=ABAC=810=45⇒Cˆ=53o7′sinC=ABAC=810=45⇒C^=53o7′
=> Aˆ=36o52′A^=36o52′
d) Xét ΔΔACM vuông tại C: CB ⊥⊥ AM
có: AC2=AB⋅AMAC2=AB⋅AM (HTL tam giác vuông)
=> AM=AC2AB=1028=12,5(cm)AM=AC2AB=1028=12,5(cm)
lại có: AB + BM = AM ; AB = 8(cm)
=> BM = 4,5(cm)
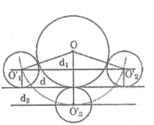
Cho đường tròn (O; 2cm) tiếp xúc với đường thẳng d. Dựng đường tròn (O’; 1cm) tiếp xúc với đường thẳng d và tiếp xúc ngoài với đường tròn (O).
* Phân tích
- Giả sử dựng được đường tròn (O’; 1cm) tiếp xúc với đường thẳng d và tiếp xúc ngoài với đường tròn (O; 2cm).
- Đường tròn (O’; 1cm) tiếp xúc với d nên O’ cách d một khoảng bằng 1cm. Khi đó O’ nằm trên hai đường thẳng d 1 , d 2 song song với d và cách d một khoảng bằng 1cm.
- Đường tròn (O’; 1cm) tiếp xúc với đường tròn (O; 2cm) nên suy ra OO’ = 3cm. Khi đó O’ là giao điểm của (O; 3cm) với d 1 và d 2
* Cách dựng
- Dựng hai đường thẳng d 1 và d 2 song song với d và cách d một khoảng bằng 1cm.
- Dựng đường tròn (O; 3cm) cắt d 1 tại O ' 1 . Vẽ ( O ' 1 ; 1cm) ta có đường tròn cần dựng
* Chứng minh
Theo cách dựng, O ' 1 cách d một khoảng bằng 1cm nên (O’1; 1cm) tiếp xúc với d.
Vì O O ' 1 = 3cm nên ( O ' 1 ; 1cm) tiếp xúc với (O; 2cm)
* Biện luận: O các d 1 một khoảng bằng 1cm nên (O; 3cm) cắt d1 tại hai điểm phân biệt.
Đúng 0
Bình luận (0)
Cho đường tròn (O; 2cm) tiếp xúc với đường thẳng d. Dựng đường tròn (O';1cm) tiếp xúc với đường thẳng d và tiếp xúc ngoài với đường tròn (O) ?
Cho đường tròn (O, R), đường kính AB. Qua A và B vẽ lần lượt hai tiếp tuyến (d) và (d’) vớiđường tròn (O). Một đường thẳng qua O cắt đường thẳng (d) ở M và cắt đường thẳng (d’) ở P. Từ O vẽmột tia vuông góc với MP và cắt đường thẳng (d’) ở N.a) Chứng minh OM OP và ΔNMP cân.b) Hạ OI vuông MN. Chứng minh OI R và MN là tiếp tuyến của (O).c) Chứng minh AM. BN R^2.d) Tìm vị trí của M để diện tích tứ giác AMNB là nhỏ nhất.
Đọc tiếp
Cho đường tròn (O, R), đường kính AB. Qua A và B vẽ lần lượt hai tiếp tuyến (d) và (d’) với
đường tròn (O). Một đường thẳng qua O cắt đường thẳng (d) ở M và cắt đường thẳng (d’) ở P. Từ O vẽ
một tia vuông góc với MP và cắt đường thẳng (d’) ở N.
a) Chứng minh OM = OP và ΔNMP cân.
b) Hạ OI vuông MN. Chứng minh OI = R và MN là tiếp tuyến của (O).
c) Chứng minh AM. BN = \(R^2\).
d) Tìm vị trí của M để diện tích tứ giác AMNB là nhỏ nhất.
Cho đường tròn (O) và đường thẳng (d) cắt đường tròn (O) tại hai điểm M; N ( đường thẳng (d) không đi qua O). Lấy điểm A thuộc đường thẳng (d) (A nằm ngoài đường tròn). Qua A kẻ hai tiếp tuyến AB và AC với đường tròn (B, C là tiếp điểm).a) Chứng minh đường tròn ngoại tiếp tam giác ABC luôn đi qua hai điểm cố định khi A di chuyển trên (d).b) Kẻ tiếp tuyến tại M và N của đường tròn (O) cắt nhau tại P. Chứng minh B; C; P thẳng hàng.c) Kẻ đường kính BOD, đường thẳng qua O vuông góc với BD cắt CD tại...
Đọc tiếp
Cho đường tròn (O) và đường thẳng (d) cắt đường tròn (O) tại hai điểm M; N ( đường thẳng (d) không đi qua O). Lấy điểm A thuộc đường thẳng (d) (A nằm ngoài đường tròn). Qua A kẻ hai tiếp tuyến AB và AC với đường tròn (B, C là tiếp điểm).a) Chứng minh đường tròn ngoại tiếp tam giác ABC luôn đi qua hai điểm cố định khi A di chuyển trên (d).b) Kẻ tiếp tuyến tại M và N của đường tròn (O) cắt nhau tại P. Chứng minh B; C; P thẳng hàng.c) Kẻ đường kính BOD, đường thẳng qua O vuông góc với BD cắt CD tại E. Chứng minh AOCE là hình thang cân
Cho đường tròn (O; R). Một đường thẳng d cắt đường tròn (O) tại hai điểm C và D. Từ một điểm I thuộc đường thẳng d, ở ngoài đường tròn (O) sao cho ID IC, kẻ hai tiếp tuyến IA và IB tới đường tròn (O). Gọi H là trung điểm của CD.1. Chứng minh năm điểm A, H, O, B, I cùng thuộc một đường tròn.2. Giả sử AI AO, khi đó tứ giác AOBI là hình gì? Tính diện tích hình tròn ngoại tiếp tứ giác AOBI? 3. Chứng minh rằng khi I di chuyển trên đường thẳng d thỏa mãn: Ở ngoài (O) và ID IC thì AB luôn đi qu...
Đọc tiếp
Cho đường tròn (O; R). Một đường thẳng d cắt đường tròn (O) tại hai điểm C và D. Từ một điểm I thuộc đường thẳng d, ở ngoài đường tròn (O) sao cho ID > IC, kẻ hai tiếp tuyến IA và IB tới đường tròn (O). Gọi H là trung điểm của CD.
1. Chứng minh năm điểm A, H, O, B, I cùng thuộc một đường tròn.
2. Giả sử AI = AO, khi đó tứ giác AOBI là hình gì? Tính diện tích hình tròn ngoại tiếp tứ giác AOBI?
3. Chứng minh rằng khi I di chuyển trên đường thẳng d thỏa mãn: Ở ngoài (O) và ID > IC thì AB luôn đi qua một điểm cố định.
1) Trong (O) có CD là dây cung không đi qua (O) và H là trung điểm CD
\(\Rightarrow OH\bot CD\Rightarrow\angle OHI=90=\angle OAI\Rightarrow OHAI\) nội tiếp
Ta có: \(\angle OAI+\angle OBI=90+90=180\Rightarrow OAIB\) nội tiếp
\(\Rightarrow O,H,A,B,I\) cùng thuộc 1 đường tròn
2) Vì IA,IB là tiếp tuyến \(\Rightarrow IB=IA=OA=OB\Rightarrow AOBI\) là hình thoi
có \(\angle OAI=90\Rightarrow AOBI\) là hình vuông
AB cắt OI tại E.Dễ chứng minh được E là trung điểm AB
Ta có: \(AB=\sqrt{OA^2+OB^2}=\sqrt{2}R\Rightarrow AE=\dfrac{\sqrt{2}}{2}R\)
\(\Rightarrow\) bán kính của (AOBI) là \(\dfrac{\sqrt{2}}{2}R\)
\(\Rightarrow\) diện tích của (AOBI) là \(\left(\dfrac{\sqrt{2}}{2}R\right)^2.\pi=\dfrac{1}{2}\pi R^2\)
3) OH cắt AB tại F
Ta có: \(\angle IEF=\angle IHF=90\Rightarrow IEHF\) nội tiếp
\(\Rightarrow OH.OF=OE.OI\) (cái này chỉ là đồng dạng thôi,bạn tự chứng minh nha)
mà \(OE.OI=OB^2=R^2\Rightarrow OF=\dfrac{R^2}{OH}\)
mà H cố định \(\Rightarrow\) F cố định \(\Rightarrow AB\) đi qua điểm F cố định 
Đúng 0
Bình luận (0)
Cho đường tròn tâm O bán kính R và đường thẳng (d) cắt đường tròn tâm O tại hai điểm C và D (đường thẳng d không đi qua tâm O). Từ điểm S bất kì thuộc tia CD (S nằm ngoài đường tròn tâm O), kẻ hai tiếp tuyến SA và SB với đường tròn tâm O (với A và B là các tiếp điểm). Gọi H là trung điểm của đoạn CD và E là giao điểm của AB với SC. Chứng minh rằng: Khi S di chuyển trên tia CD (S nằm ngoài đường tròn tâm O) thì đường thẳng AB luôn đi qua 1 điểm cố định
Đọc tiếp
Cho đường tròn tâm O bán kính R và đường thẳng (d) cắt đường tròn tâm O tại hai điểm C và D (đường thẳng d không đi qua tâm O). Từ điểm S bất kì thuộc tia CD (S nằm ngoài đường tròn tâm O), kẻ hai tiếp tuyến SA và SB với đường tròn tâm O (với A và B là các tiếp điểm). Gọi H là trung điểm của đoạn CD và E là giao điểm của AB với SC. Chứng minh rằng: Khi S di chuyển trên tia CD (S nằm ngoài đường tròn tâm O) thì đường thẳng AB luôn đi qua 1 điểm cố định
20 tháng 5 2021 lúc 18:37
Cho đường tròn tâm O, đường kính AB và d là một tiếp tuyến của đường tròn (O) tại điểm A. Trên đường thẳng d lấy điểm M (khác A) và trên đoạn OB lấy điểm N (khác O và B). Đường thẳng MN cắt đường tròn (O) tại hai điểm C và D sao cho C nằm giữa M và D. Gọi H là trung điểm của đoạn thẳng CD.a) Chứng minh tứ giác AOHM nội tiếp được trong đường tròn.c) Đường thẳng BC cắt đường thẳng OM tại I. Chứng minh rằng đường thẳng AI song song với đường thẳng BD.
Đọc tiếp
Cho đường tròn tâm O, đường kính AB và d là một tiếp tuyến của đường tròn (O) tại điểm A. Trên đường thẳng d lấy điểm M (khác A) và trên đoạn OB lấy điểm N (khác O và B). Đường thẳng MN cắt đường tròn (O) tại hai điểm C và D sao cho C nằm giữa M và D. Gọi H là trung điểm của đoạn thẳng CD.
a) Chứng minh tứ giác AOHM nội tiếp được trong đường tròn.
c) Đường thẳng BC cắt đường thẳng OM tại I. Chứng minh rằng đường thẳng AI song song với đường thẳng BD.
Cho đường tròn tâm O, đường kính AB và d là một tiếp tuyến của đường tròn (O) tại điểm A. Trên đường thẳng d lấy điểm M (khác A) và trên đoạn OB lấy điểm N (khác O và B). Đường thẳng MN cắt đường tròn (O) tại hai điểm C và D sao cho C nằm giữa M và D. Gọi H là trung điểm của đoạn thẳng CD.a) Chứng minh tứ giác AOHM nội tiếp được trong đường tròn. c) Đường thẳng BC cắt đường thẳng OM tại I. Chứng minh rằng đường thẳng AI song song với đường thẳng BD.
Đọc tiếp
Cho đường tròn tâm O, đường kính AB và d là một tiếp tuyến của đường tròn (O) tại điểm A. Trên đường thẳng d lấy điểm M (khác A) và trên đoạn OB lấy điểm N (khác O và B). Đường thẳng MN cắt đường tròn (O) tại hai điểm C và D sao cho C nằm giữa M và D. Gọi H là trung điểm của đoạn thẳng CD.
a) Chứng minh tứ giác AOHM nội tiếp được trong đường tròn.
c) Đường thẳng BC cắt đường thẳng OM tại I. Chứng minh rằng đường thẳng AI song song với đường thẳng BD.
Cho đường tròn (O;R), đường kính AB. Qua A và B vẽ lần lượt hai tiếp tuyến (d) và (d) với đường tròn O. Một đường thẳng qua O cắt đường thẳng (d) ở M và cắt đường thẳng (d) ở P. Từ O vẽ một tia vuông góc với MP cắt đường thẳng (d) ở N.a) cm rằng: OM OP và tam giác NMP cânb) Hạ OI vuông góc với MN. Hãy cm rằng OI R và MN là tiếp tuyến của đường tròn (O)c) cm: AM.BNR^2
Đọc tiếp
Cho đường tròn (O;R), đường kính AB. Qua A và B vẽ lần lượt hai tiếp tuyến (d) và (d') với đường tròn O. Một đường thẳng qua O cắt đường thẳng (d) ở M và cắt đường thẳng (d') ở P. Từ O vẽ một tia vuông góc với MP cắt đường thẳng (d') ở N.
a) cm rằng: OM = OP và tam giác NMP cân
b) Hạ OI vuông góc với MN. Hãy cm rằng OI =R và MN là tiếp tuyến của đường tròn (O)
c) cm: AM.BN=R^2