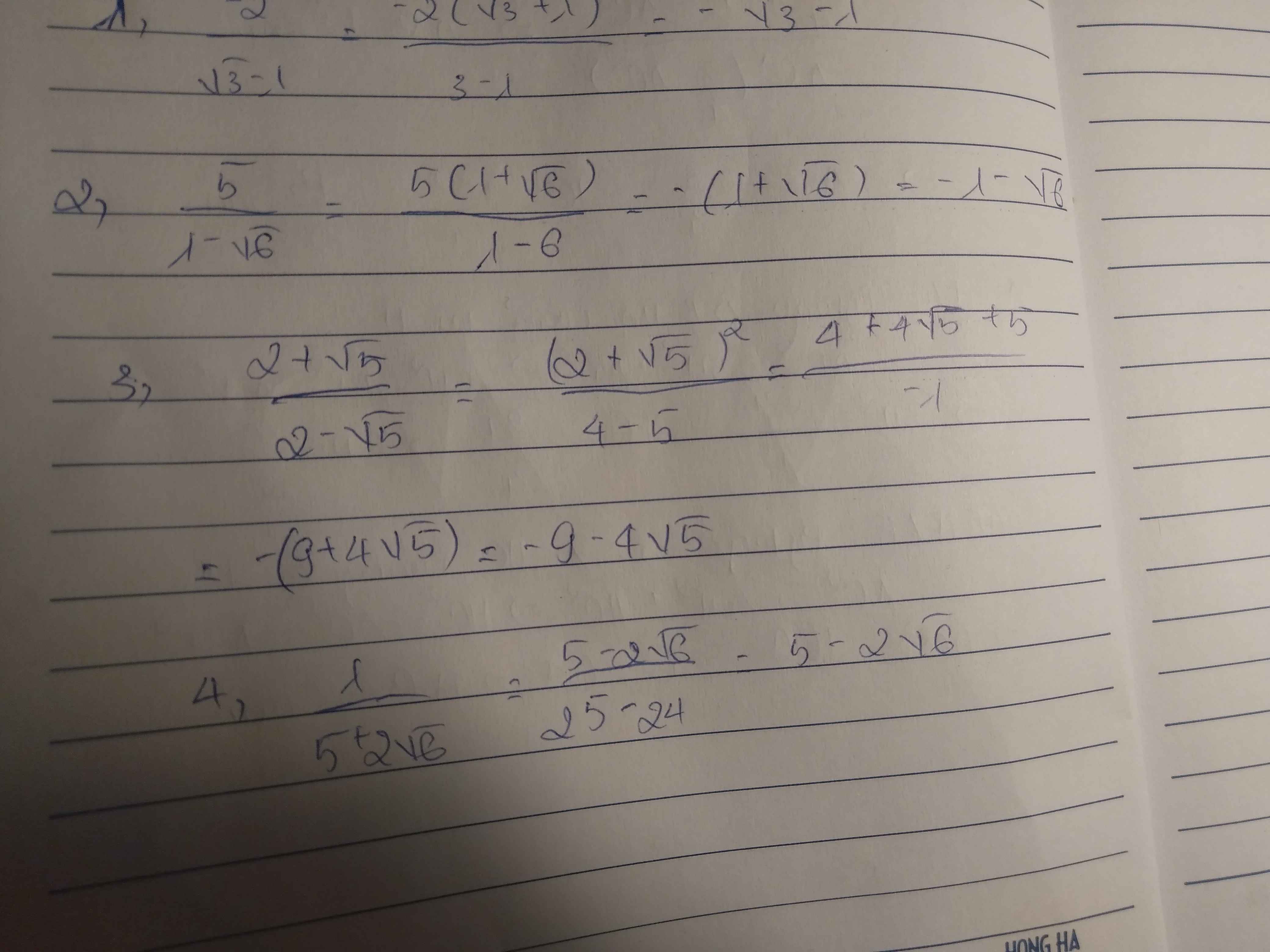\(\sqrt{6+2\sqrt{5}}+\sqrt{6-2\sqrt{5}}\)

Những câu hỏi liên quan
x^3left(sqrt[3]{5+2sqrt{6}}+sqrt[3]{5-2sqrt{6}}right)^3sqrt[3]{5+2sqrt{6}}^3+3sqrt[3]{left(5+2sqrt{6}right)^2}.sqrt[3]{5-2sqrt{6}}+3sqrt[3]{5+2sqrt{6}}.sqrt[3]{left(5-2sqrt{6}right)^2}+sqrt[3]{5-2sqrt{6}}^35+2sqrt{6}+3sqrt[3]{left(5+2sqrt{6}right)left(5-2sqrt{6}right)}.sqrt[3]{5+2sqrt{6}}+3sqrt[3]{left(5+2sqrt{6}right)left(5-2sqrt{6}right)}.sqrt[3]{5-2sqrt{6}}+5-2sqrt{6}5+5+3sqrt[3]{left(25-4.6right)}.sqrt[3]{5+2sqrt{6}}+3sqrt[3]{left(25-4.6right)}.sqrt[3]{5-2sqrt{6}}10+
3sqrt[3]{5+2sqrt{6}}+3sq...
Đọc tiếp
\(x^3=\left(\sqrt[3]{5+2\sqrt{6}}+\sqrt[3]{5-2\sqrt{6}}\right)^3=\sqrt[3]{5+2\sqrt{6}}^3\)
\(+3\sqrt[3]{\left(5+2\sqrt{6}\right)^2}.\sqrt[3]{5-2\sqrt{6}}+3\sqrt[3]{5+2\sqrt{6}}.\sqrt[3]{\left(5-2\sqrt{6}\right)^2}+\sqrt[3]{5-2\sqrt{6}}^3\)
\(=5+2\sqrt{6}+3\sqrt[3]{\left(5+2\sqrt{6}\right)\left(5-2\sqrt{6}\right)}.\sqrt[3]{5+2\sqrt{6}}\)
\(+3\sqrt[3]{\left(5+2\sqrt{6}\right)\left(5-2\sqrt{6}\right)}.\sqrt[3]{5-2\sqrt{6}}+5-2\sqrt{6}\)
\(=5+5+3\sqrt[3]{\left(25-4.6\right)}.\sqrt[3]{5+2\sqrt{6}}+3\sqrt[3]{\left(25-4.6\right)}.\sqrt[3]{5-2\sqrt{6}}\)
\(=10+ 3\sqrt[3]{5+2\sqrt{6}}+3\sqrt[3]{5-2\sqrt{6}}\)
p/s : có bạn hỏi nên mình đăng , các bạn đừng report nhé
\(\sqrt{\left(\sqrt{7}-5\right)^2}+\sqrt{\left(2-\sqrt{7}\right)^2}\)
\(\sqrt{11+6\sqrt{2}}-\sqrt{11-6\sqrt{2}}\)
\(\sqrt{17+12\sqrt{2}}+\sqrt{17-12\sqrt{2}}\)
\(\sqrt{6+2\sqrt{5}}-\sqrt{6-2\sqrt{5}}\)
Lời giải:
a. \(=|\sqrt{7}-5|+|2-\sqrt{7}|=5-\sqrt{7}+(\sqrt{7}-2)=3\)
b. \(=\sqrt{(3+\sqrt{2})^2}-\sqrt{(3-\sqrt{2})^2}=|3+\sqrt{2}|-|3-\sqrt{2}|\)
\(=(3+\sqrt{2})-(3-\sqrt{2})=2\sqrt{2}\)
c.
\(=\sqrt{(3+2\sqrt{2})^2}+\sqrt{(3-2\sqrt{2})^2}=|3+2\sqrt{2}|+|3-2\sqrt{2}|\)
$=(3+2\sqrt{2})+(3-2\sqrt{2})=6$
d.
$=\sqrt{(\sqrt{5}+1)^2}-\sqrt{(\sqrt{5}-1)^2}$
$=|\sqrt{5}+1|-|\sqrt{5}-1|=\sqrt{5}+1-(\sqrt{5}-1)=2$
Đúng 3
Bình luận (0)
1, Rút gọn: A = \(\sqrt{5+2\sqrt{6}}-\sqrt{5-2\sqrt{6}}\)
2, Giải phương trình: \(\sqrt{4x^2-12x+9}=\sqrt{5+2\sqrt{6}}-\sqrt{5-2\sqrt{6}}\)
Câu 1:
\(A=\sqrt{3}+\sqrt{2}-\sqrt{3}+\sqrt{2}=2\sqrt{2}\)
Câu 2:
\(\Leftrightarrow\left|2x-3\right|=\sqrt{3}+\sqrt{2}-\sqrt{3}+\sqrt{2}=2\sqrt{3}\)
\(\Leftrightarrow\left[{}\begin{matrix}2x-3=2\sqrt{3}\\2x-3=-2\sqrt{3}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{2\sqrt{3}+3}{2}\\x=\dfrac{-2\sqrt{3}+3}{2}\end{matrix}\right.\)
Đúng 0
Bình luận (0)
`1)A=\sqrt{5+2\sqrt{6}}-\sqrt{5-2\sqrt{6}}`
`A=\sqrt{3+2\sqrt{3}.\sqrt{2}+2}-\sqrt{3-2\sqrt{3}.\sqrt{2}+2}`
`A=\sqrt{(\sqrt{3}+\sqrt{2})^2}-\sqrt{(\sqrt{3}-\sqrt{2})^2}`
`A=|\sqrt{3}+\sqrt{2}|-|\sqrt{3}-\sqrt{2}|`
`A=\sqrt{3}+\sqrt{2}-\sqrt{3}+\sqrt{2}=2\sqrt{2}`
_________________________________________________
`2)\sqrt{4x^2-12x+9}=\sqrt{5+2\sqrt{6}}-\sqrt{5-2\sqrt{6}}`
`<=>\sqrt{4x^2-12x+9}=2\sqrt{2}` (Như câu `1`)
`<=>4x^2-12x+9=8`
`<=>4x^2-12x+1=0`
Ptr có:`\Delta'=(-6)^2-4=32 > 0`
`=>` Ptr có `2` nghiệm pb
`x_1=[-b+\sqrt{\Delta'}]/a=[-(-6)+\sqrt{32}]/4=[3+2\sqrt{2}]/2`
`x_2=[-b-\sqrt{\Delta'}]/a=[-(-6)-\sqrt{32}]/4=[3-2\sqrt{2}]/2`
Vậy `S={[3+-2\sqrt{2}]/2}`
Đúng 1
Bình luận (0)
Rút gọn: ( 2,5 Điểm )A dfrac{sqrt{6+2sqrt{5}}}{sqrt{5}+1}+ dfrac{sqrt{5-2sqrt{6}}}{sqrt{3}-sqrt{2}}B dfrac{3}{sqrt{5}-2}+ dfrac{4}{sqrt{6}+sqrt{2}}+ dfrac{1}{sqrt{6}+sqrt{5}}C dfrac{1}{sqrt{1}+sqrt{2}}+dfrac{1}{sqrt{2}+sqrt{3}}+dfrac{1}{sqrt{3}+sqrt{4}}+...+dfrac{1}{sqrt{99}+sqrt{100}}D dfrac{1}{2-sqrt{3}}+sqrt{7-4sqrt{3}}E sqrt{dfrac{3sqrt{3}-4}{2sqrt{3}+1}}-sqrt{dfrac{sqrt{3}+4}{5-2sqrt{3}}}F dfrac{1}{2+sqrt{3}}+dfrac{sqrt{2}}{sqrt{6}}-dfrac{2}{3+sqrt{3}}
Đọc tiếp
Rút gọn: ( 2,5 Điểm )
A= \(\dfrac{\sqrt{6+2\sqrt{5}}}{\sqrt{5}+1}\)+ \(\dfrac{\sqrt{5-2\sqrt{6}}}{\sqrt{3}-\sqrt{2}}\)
B= \(\dfrac{3}{\sqrt{5}-2}\)+ \(\dfrac{4}{\sqrt{6}+\sqrt{2}}\)+ \(\dfrac{1}{\sqrt{6}+\sqrt{5}}\)
C = \(\dfrac{1}{\sqrt{1}+\sqrt{2}}+\dfrac{1}{\sqrt{2}+\sqrt{3}}+\dfrac{1}{\sqrt{3}+\sqrt{4}}+...+\dfrac{1}{\sqrt{99}+\sqrt{100}}\)
D= \(\dfrac{1}{2-\sqrt{3}}+\sqrt{7-4\sqrt{3}}\)
E = \(\sqrt{\dfrac{3\sqrt{3}-4}{2\sqrt{3}+1}}-\sqrt{\dfrac{\sqrt{3}+4}{5-2\sqrt{3}}}\)
F = \(\dfrac{1}{2+\sqrt{3}}+\dfrac{\sqrt{2}}{\sqrt{6}}-\dfrac{2}{3+\sqrt{3}}\)
a: \(E=1+1=2\)
b: \(=6+3\sqrt{5}+\sqrt{6}-\sqrt{2}+\sqrt{6}-\sqrt{5}\)
\(=6+2\sqrt{6}-\sqrt{2}+2\sqrt{5}\)
d: \(=2+\sqrt{3}+2-\sqrt{3}=4\)
Đúng 1
Bình luận (0)
1. dfrac{-2}{sqrt{3}-1}2. dfrac{5}{1-sqrt{6}}3. dfrac{2+sqrt{5}}{2-sqrt{5}}4. dfrac{1}{5+2sqrt{6}}5. dfrac{sqrt{5}+2}{sqrt{5}-2}6. dfrac{5sqrt{2}-2sqrt{5}}{sqrt{2}-sqrt{5}}7. dfrac{sqrt{20}-3sqrt{10}}{3-sqrt{2}}8. dfrac{6-2sqrt{5}}{3+sqrt{5}}9. dfrac{9+4sqrt{5}}{sqrt{5}+2}
Đọc tiếp
1. \(\dfrac{-2}{\sqrt{3}-1}\)
2. \(\dfrac{5}{1-\sqrt{6}}\)
3. \(\dfrac{2+\sqrt{5}}{2-\sqrt{5}}\)
4. \(\dfrac{1}{5+2\sqrt{6}}\)
5. \(\dfrac{\sqrt{5}+2}{\sqrt{5}-2}\)
6. \(\dfrac{5\sqrt{2}-2\sqrt{5}}{\sqrt{2}-\sqrt{5}}\)
7. \(\dfrac{\sqrt{20}-3\sqrt{10}}{3-\sqrt{2}}\)
8. \(\dfrac{6-2\sqrt{5}}{3+\sqrt{5}}\)
9. \(\dfrac{9+4\sqrt{5}}{\sqrt{5}+2}\)
rút gọn
\(\sqrt{3}+\sqrt{11+6\sqrt{ }2}-\sqrt{5}+2\sqrt{6}\)\(\sqrt{2}+\sqrt{6+2\sqrt{ }5}-\sqrt{7+2\sqrt{ }10}\)
\(\sqrt{6+\sqrt{ }6+\sqrt{ }6+\sqrt{ }6........}\)
\(\sqrt{3+\sqrt{ }5+2\sqrt{ }3}+\sqrt{3-\sqrt{ }5+2\sqrt{ }3}\)
\(\sqrt{227-30\sqrt{ }2}+\sqrt{123}+22\sqrt{2}\)
\(\sqrt{3-2\sqrt{2}}-\sqrt{11+6\sqrt{2}}\)
\(\sqrt{4-2\sqrt{3}}-\sqrt{7-4\sqrt{3}}+\sqrt{19+8\sqrt{3}}\)
\(\sqrt{6-2\sqrt{5}}+\sqrt{9+4\sqrt{5}}-\sqrt{14-6\sqrt{5}}\)
\(\sqrt{11-4\sqrt{7}}+\sqrt{23-8\sqrt{7}}+\sqrt{\left(-2^6\right)}\)
rút gọn:giải chi tiết hộ mình nha
a) Ta có: \(\sqrt{3-2\sqrt{2}}-\sqrt{11+6\sqrt{2}}\)
\(=\sqrt{2}-1-3-\sqrt{2}\)
=-4
b) Ta có: \(\sqrt{4-2\sqrt{3}}-\sqrt{7-4\sqrt{3}}+\sqrt{19+8\sqrt{3}}\)
\(=\sqrt{3}-1-2+\sqrt{3}+4+\sqrt{3}\)
\(=3\sqrt{3}+1\)
c) Ta có: \(\sqrt{6-2\sqrt{5}}+\sqrt{9+4\sqrt{5}}-\sqrt{14-6\sqrt{5}}\)
\(=\sqrt{5}-1+\sqrt{5}-2-3+\sqrt{5}\)
\(=3\sqrt{5}-6\)
d) Ta có: \(\sqrt{11-4\sqrt{7}}+\sqrt{23-8\sqrt{7}}+\sqrt{\left(-2\right)^6}\)
\(=\sqrt{7}-2+4-\sqrt{7}+8\)
=10
Đúng 1
Bình luận (0)
\(a:\sqrt{\left(\sqrt{3}-2\right)^2}+\sqrt{5+2\sqrt{6}}\)
b : \(\dfrac{\sqrt{6}-\sqrt{2}}{\sqrt{3}-1}-\sqrt{2}\)
c : \(\left(2+\dfrac{5-2\sqrt{5}}{2-\sqrt{5}}\right).\left(2+\dfrac{5-3\sqrt{5}}{3-\sqrt{5}}\right)\)
d : \(\left(\dfrac{15}{\sqrt{6}+1}+\dfrac{4}{\sqrt{6}-2}-\dfrac{12}{3-\sqrt{6}}\right).\left(\sqrt{6}+11\right)\)
a) \(\sqrt{\left(\sqrt{3}-2\right)^2}+\sqrt{5+2\sqrt{6}}\)
\(=\left|\sqrt{3}-2\right|+\sqrt{\left(\sqrt{3}\right)^2+2\cdot\sqrt{3}\cdot\sqrt{2}+\left(\sqrt{2}\right)^2}\)
\(=\left(\sqrt{3}-\sqrt{2}\right)+\sqrt{\left(\sqrt{3}+\sqrt{2}\right)^2}\)
\(=\sqrt{3}-\sqrt{2}+\sqrt{3}+\sqrt{2}\)
\(=2\sqrt{3}\)
b) \(\dfrac{\sqrt{6}-\sqrt{2}}{\sqrt{3}-1}-\sqrt{2}\)
\(=\dfrac{\sqrt{2}\left(\sqrt{3}-1\right)}{\sqrt{3}-1}-\sqrt{2}\)
\(=\sqrt{2}-\sqrt{2}\)
\(=0\)
c) \(\left(2+\dfrac{5-2\sqrt{5}}{2-\sqrt{5}}\right)\cdot\left(2+\dfrac{5-3\sqrt{5}}{3-\sqrt{5}}\right)\)
\(=\left[2-\dfrac{\sqrt{5}\left(2-\sqrt{5}\right)}{2-\sqrt{5}}\right]\cdot\left[2-\dfrac{\sqrt{5}\left(3-\sqrt{5}\right)}{3-\sqrt{5}}\right]\)
\(=\left(2-\sqrt{5}\right)\left(2-\sqrt{5}\right)\)
\(=4-4\sqrt{5}+5\)
\(=9-4\sqrt{5}\)
d) \(\left(\dfrac{15}{\sqrt{6}+1}+\dfrac{4}{\sqrt{6}-2}-\dfrac{12}{3-\sqrt{6}}\right)\left(\sqrt{6}+11\right)\)
\(=\left[\dfrac{15\left(\sqrt{6}-1\right)}{\left(\sqrt{6}+1\right)\left(\sqrt{6}-1\right)}+\dfrac{4\left(\sqrt{6}+2\right)}{\left(\sqrt{6}-2\right)\left(\sqrt{6}+2\right)}-\dfrac{12\left(3+\sqrt{6}\right)}{\left(3-\sqrt{6}\right)\left(3+\sqrt{6}\right)}\right]\left(\sqrt{6}+11\right)\)
\(=\left[\dfrac{15\left(\sqrt{6}-1\right)}{5}+\dfrac{4\left(\sqrt{6}+2\right)}{6-4}-\dfrac{12\left(3+\sqrt{6}\right)}{9-6}\right]\left(\sqrt{6}+11\right)\)
\(=\left(3\sqrt{6}-3+2\sqrt{6}+4-12-4\sqrt{6}\right)\left(\sqrt{6}+11\right)\)
\(=\left(\sqrt{6}-11\right)\left(\sqrt{6}+11\right)\)
\(=6-121\)
\(=-115\)
Đúng 1
Bình luận (0)
* Thực hiện phép tính:
a. \(\dfrac{\sqrt{7}-5}{2}-\dfrac{6-2\sqrt{7}}{4}+\dfrac{6}{\sqrt{7}-2}-\dfrac{5}{4+\sqrt{7}}\)
b. \(\dfrac{2}{\sqrt{6}-2}+\dfrac{2}{\sqrt{6}+2}+\dfrac{5}{\sqrt{6}}\)
c. \(\dfrac{1}{\sqrt{3}+\sqrt{2}-\sqrt{5}}-\dfrac{1}{\sqrt{3}+\sqrt{2}+\sqrt{5}}\)
\(a,=\dfrac{\sqrt{7}-5}{2}-\dfrac{3-\sqrt{7}}{2}+\dfrac{6\left(\sqrt{7}+2\right)}{3}-\dfrac{5\left(4-\sqrt{7}\right)}{9}\\ =\dfrac{\sqrt{7}-5-3+\sqrt{7}}{2}+2\sqrt{7}+4-\dfrac{20-5\sqrt{7}}{9}\\ =\dfrac{2\sqrt{7}-8}{2}+2\sqrt{7}+4-\dfrac{20-5\sqrt{7}}{9}\\ =\sqrt{7}-4+2\sqrt{7}+4-\dfrac{20-5\sqrt{7}}{9}\\ =\dfrac{27\sqrt{7}-20+5\sqrt{7}}{9}=\dfrac{32\sqrt{7}-20}{9}\)
\(b,=\dfrac{2\left(\sqrt{6}+2\right)}{2}+\dfrac{2\left(\sqrt{6}-2\right)}{2}+\dfrac{5\sqrt{6}}{6}\\ =\sqrt{6}+2+\sqrt{6}-2+\dfrac{5\sqrt{6}}{6}\\ =\dfrac{12\sqrt{6}+5\sqrt{6}}{6}=\dfrac{17\sqrt{6}}{6}\)
\(c,=\dfrac{\sqrt{3}+\sqrt{2}+\sqrt{5}-\sqrt{3}-\sqrt{2}+\sqrt{5}}{\left(\sqrt{3}+\sqrt{2}\right)^2-5}\\ =\dfrac{2\sqrt{5}}{5+2\sqrt{6}-5}=\dfrac{2\sqrt{5}}{2\sqrt{6}}=\dfrac{\sqrt{30}}{6}\)
Đúng 2
Bình luận (0)
\(\sqrt{5+2\sqrt{6}}-\sqrt{5-2\sqrt{6}}\)
\(\sqrt{7+4\sqrt{3}}-\sqrt{\left(2-\sqrt{5}\right)^2}-\sqrt{21-8\sqrt{5}}\)
\(\sqrt{5+2\sqrt{6}}-\sqrt{5-2\sqrt{6}}\)
\(=\sqrt{\left(\sqrt{3}\right)^2+2\cdot\sqrt{3}\cdot\sqrt{2}+\left(\sqrt{2}\right)^2}-\sqrt{\left(\sqrt{3}\right)^2-2\cdot\sqrt{3}\cdot\sqrt{2}+\left(\sqrt{2}\right)^2}\)
\(=\sqrt{\left(\sqrt{3}+\sqrt{2}\right)^2}-\sqrt{\left(\sqrt{3}-\sqrt{2}\right)^2}\)
\(=\left|\sqrt{3}+\sqrt{2}\right|-\left|\sqrt{3}-\sqrt{2}\right|\)
\(=\sqrt{3}+\sqrt{2}-\sqrt{3}+\sqrt{2}\)
\(=2\sqrt{2}\)
Đúng 0
Bình luận (0)
a: \(=\sqrt{\left(\sqrt{3}+\sqrt{2}\right)^2}-\sqrt{\left(\sqrt{3}-\sqrt{2}\right)^2}\)
\(=\sqrt{3}+\sqrt{2}-\sqrt{3}+\sqrt{2}=2\sqrt{2}\)
b: \(=\sqrt{\left(2+\sqrt{3}\right)^2}-\sqrt{5}+2-4+\sqrt{5}\)
\(=2+\sqrt{3}-2=\sqrt{3}\)
Đúng 0
Bình luận (0)
\(\sqrt{7+4\sqrt{3}}-\sqrt{\left(2-\sqrt{5}\right)^2}-\sqrt{21-8\sqrt{5}}\)
\(=\sqrt{2^2+2\cdot2\cdot\sqrt{3}+\left(\sqrt{3}\right)^2}-\left|2-\sqrt{5}\right|-\sqrt{4^2-2\cdot4\cdot\sqrt{5}+\left(\sqrt{5}\right)^2}\)
\(=\sqrt{\left(2+\sqrt{3}\right)^2}+\left(2-\sqrt{5}\right)-\sqrt{\left(4-\sqrt{5}\right)^2}\)
\(=\left|2+\sqrt{3}\right|+2-\sqrt{5}-\left|4-\sqrt{5}\right|\)
\(=2+\sqrt{3}+2-\sqrt{5}-4+\sqrt{5}\)
\(=\sqrt{3}\)
Đúng 0
Bình luận (0)